Diodengepumpter, frequenzverdoppelter Nd:YVO4

Institut für Angewandte Optik und Elektronik
Fakultät für Informations-, Medien- und Elektrotechnik
Fachhochschule Köln
Praktikumsanleitung zum Fach Lasertechnik
Diodengepumpter, frequenzverdoppelter
Nd:YVO4-Laser
Köln, 12. September 2010
1 Versuchsziel
In diesem Versuch werden physikalische Eigenschaften von zwei wichtigen Arten von Festkörperlasern untersucht: dem Halbleiterlaser (Laserdiode) und dem Festkörperlaser (Nd:YVO4
Neodym Yttrium Vanadat). Der Halbleiterlaser dient in diesem Versuch zum optischen Pumpen des Nd:YVO4 -Lasers. Durch diese Konfiguration sind extrem kompakte Festkörperlaser
möglich geworden, die hohe Ausgangsleistungen erlauben oder selbst in Laserpointern Platz
finden.
Um den Nd:YVO4 -Kristall effektiv pumpen zu können, wird dessen Absorptionsverhalten bei
Variation des Injektionsstromes vermessen. Schließlich dient die im Resonator vorhandene
hohe Intensität dazu, effiziente nichtlineare Wechselwirkung von Strahlung mit Materie zur
Erzeugung von Licht doppelter Frequenz hervorzurufen. Hierzu wird die Strahlungsfrequenz
des Nd:YVO4 -Lasers mittels eines KTP-Kristalls (Kalium-Titanyl-Phosphat KTiOPO4) verdoppelt. Anhand dieses Aufbaus und des so erzeugten grünen Lichtes können einige grundlegende nichtlineare optische Eigenschaften demonstriert werden.
2 Grundlagen
2.1 Nichtlineare Medien
Nichtlineare Phänomene resultieren aus der Tatsache, dass die atomaren elektrischen Dipole
der Materie nicht mehr linear auf die hohen elektrischen Wechselfelder der Lichtwelle antworten können. Die ein Medium durchquerende, hochfrequente Lichtwelle bewirkt Ladungsverschiebungen und führt damit zu influenzierten elektrischen Dipolen und einer elektrischen
Polarisation des Mediums. Diese wird im Bereich der hohen Frequenzen des sichtbaren Lichts
(ν ≈ 500THz) fast ausschließlich von den Elektronen der äußeren Atomhülle hervorgerufen,
da die schweren Kerne und die fest gebundenen inneren Elektronen kaum verschoben werden. Bei kleinen Schwingungsamplituden der Elektronen ist die Polarisation proportional zum
E-Feld der Welle. Diese strenge Proportionalität wird bei größeren Intensitäten verletzt, analog zum Verhalten einer einfachen Feder, deren Anharmonizität mit steigender Auslenkung
wächst.
In einem linearen Medium besteht zwischen der Polarisation P -dem elektrischen Dipolmoment des Mediums pro Volumeneinheit- und dem polarisierenden elektrischen Feld E der
Zusammenhang:
~P = ε0 χ ~E
(2.1)
hierbei ist χ die feldstärkeunabhängige (elektrische) Suszeptibilität und ε0 die elektrische
Feldkonstante des Vakuums. Nichtlinearität kann man durch eine feldabhängige Suszeptibilität χ(E) beschreiben, die wir für kleine Störungen in eine Potenzreihe entwickeln:
Suszeptibilit ät
χ(E) = χ1 + χ2 E + χ3 E 2 ...
(2.2)
Einsetzen in 2.2 ergibt für die
Polarisation
P = ε0 χ1 E + ε0 χ2 E 2 + ε0 χ3 E 3 ...
| {z } | {z } | {z }
P1
P2
(2.3)
P3
Die linearen (χ1 ) und nichtlinearen (χ2 ,χ3 ...) Suszeptibilitätskoeffizienten charakterisieren
die optischen Eigenschaften des Mediums; P ist die nichtlineare Antwort des Systems auf das
erregende Feld E. Der erste Term P1 in 2.3 umfasst die lineare Optik, in der die Polarisation einfach proportional zum E-Feld ist. Höhere Terme beeinflussen die Polarisation nur bei
sehr starken E-Feldern merklich und wurden meist erst seit der Erfindung des Lasers expe-
2
rimentell zugänglich. Das kohärente Laserlicht kann auf Volumina der Größenordnung einer
Wellenlänge fokussiert werden, hierbei entstehen elektrische Feldstärken größer 1010V /m, die
vergleichbar sind mit den Feldern, mit denen die Elektronen an die Kerne gebunden sind.
Peter Franken und seine Mitarbeiter führten 1961 an der Universität von Michigan das erste Experiment zur nichtlinearen kohärenten Optik aus. Das Team fokussierte das kohärente Licht eines gepulsten Rubinlasers von 694,3nm Wellenlänge auf einen Quarzkristall und
wies Frequenzverdopplung nach, indem es eine schwache ultraviolette Ausgangsstrahlung von
347,15nm - also mit halber Wellenlänge bzw. doppelter Frequenz - registrierte.
2.2 Frequenzverdopplung
Frequenzverdopplung (Erzeugung der zweiten Harmonischen, Second Harmonic Generation,
SHG) resultiert aus dem Term 2. Ordnung in 2.3:
quadratische Nichtlinearit ät
P2 = ε0 χ2 E 2
(2.4)
bei dem die Polarisation quadratisch von der Feldstärke abhängt.
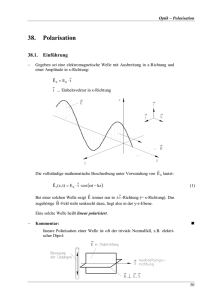
Abb. 1: Lineare (P1 ), quadratische (P2 ) und typische nichtlineare Antwort der Polarisation P auf ein
elektrisches Feld. Im nichtlinearen Fall rufen Felder gleicher Größe, aber verschiedenen Vorzeichens
unterschiedliche Antworten (Kurve P) hervor. Für den gezeichneten Fall quadratischer Nichtlinearität
(mit P = P1 + P2 und χ2 < 0) bewirken negative Felder eine stärkere Polarisation als positive Felder
gleicher Größe.
3
Abb. 2: Anregendes E-Feld (a), nicht symmetrische Polarisation (b) und deren FourierKomponenten Pω (c), P2 ω (d) so wie der
Gleichanteil P (e).
Abb.1 zeigt die Kennlinie der Polarisation als Funktion der Feldstärke: Die Gesamtpolarisation
P1 + P2 stimmt bei kleinen Feldstärken mit der linearen Polarisation überein und unterscheidet
sich bei großen Feldstärken aufgrund des quadratischen Terms P2 .
Mathematisch kann die Erzeugung der 2. Harmonischen leicht erklärt werden. Das einwirkende E-Feld sei
E = Ê cos(ωt) = Ê
e jωt + e− jωt
2
(2.5)
Einsetzen in 2.4 gibt (mit cos2 α = 21 (1+cos2α)) für den quadratischen Term der Polarisation:
1
1
P2 = ε0 χ2 Ê 2 cos2 (ωt) = ε0 χ2 Ê 2 + ε0 χ2 Ê 2 cos(2ωt)
2
2
(2.6)
Man erhält also einen zeitunabhängigen Term, der die optische Gleichrichtung beschreibt,
und einen Term, der die doppelte Anregungsfrequenz enthält. Dementsprechend erzeugen die
von der Primärwelle angeregten Dipole elektromagnetische Strahlung der Frequenz 2ω, die
dann in der austretenden Strahlung zusammen mit der im Allgemeinen wesentlich stärkeren
Strahlung aus der linearen Wechselwirkung (mit der Grundfrequenz ω) enthalten ist (s. Abb.
2).
4
Verfolgen wir in einem nichtlinearen Medium eine Wellenfront der Primärwelle von der Oberfläche bis zu einem Punkt im Abstand l, so überlagern sich dort unter anderem die von der
Wellenfront entlang dieses Weges erzeugten Teilwellen der Frequenz 2ω. Konstruktive Interferenz ist nur dann gegeben, wenn sich die Oberwelle genauso schnell wie die sie erzeugende
Grundwelle ausbreitet, wenn also für die Phasengeschwindigkeiten c2ω = cω gilt. Aufgrund
der Dispersion wird dies jedoch im Allgemeinen nicht der Fall sein; es kommt zu Phasenunterschieden der 2ω-Teilwellen und unter Umständen zur Auslöschung.
Um dies zu verstehen, wählen wir einen Kristall mit der Länge l = 2lK . Die nun an den Orten
l = 0 und l = 2lK durch eine Welle erzeugten, frequenzverdoppelten Teilwellen weisen einen
Gangunterschied ∆min = λ2ω = λω /2 auf. Somit sind die Gangunterschiede der auf der Länge
2lK entstandenen Teilwellen kontinuierlich zwischen 0 und λ2ω verteilt. Hieraus folgt, dass
am Ausgang des Kristalls zu jeder Teilwelle eine um λ2ω /2 verschobene Teilwelle existiert,
welche sich gegenseitig durch destruktive Interferenz auslöschen.
Abb. 3: Die durch eine Welle kontinuierlich erzeugten frequenzverdoppelten Teilwellen löschen sich
bei einer Kristalllänge, die der doppelten Kristallkohärenzlänge entspricht aus. Die mit d.I. (destruktive Interferenz) gekennzeichneten Stellen markieren Entstehungsorte sich gegenseitig auslöschender
Teilwellen.
Maximale Intensität muss dann bei ∆max = λ2ω /2 = λω /4 - entsprechend l = lK - auftreten.
Der Gangunterschied ist gleich der Differenz der optischen Wege und wir erhalten:
∆max =
λω
= (n2ω − nω )lK
4
5
(2.7)
Hieraus folgt mit ∆n = |n2ω − nω | die
Kristallkohärenzl änge
lK =
λω
4∆n
(2.8)
Wir hatten gesehen, dass bei der Kristalldicke lK die maximale Intensität der 2. Harmonischen
auftritt. Der Vorgang der Verstärkung und Auslöschung wiederholt sich mit zunehmender Länge l periodisch, so dass für die zur Polarisation P2 proportionale Feldstärke der Oberwelle gilt:
Ê2ω ∼ P2 ∼
χ2 Êω2 lK sin
π
l
2lK
(2.9)
Berücksichtigt man nun die Intensitätsabnahme der Grundwelle (Êω2 ) auf Grund der Wechselwirkung mit dem frequenzverdopplenden Kristall fällt die registrierte Intensität bei steigender
Kristalldicke rasch ab, so dass diese zur effizienten Frequenzverdopplung nur wenige Kristallkohärenzlängen betragen darf (siehe Abb.4).
Abb. 4: Abnahme der emittierten Feldstärke einer Frequenzverdopplung bei steigender Kristallänge l
und einer Kristallkohärenlänge von 10µm
Der Nachteil der hierdurch benötigten kurzen Kristallkohärenzlänge (siehe Aufgabe 3.1) kann
mit Hilfe der Doppelbrechung der Kristalle umgangen werden. Die Brechzahl und Geschwindigkeit des außerordentlichen Strahls hängt von seiner Richtung relativ zur optischen Achse
des Kristalls ab.
Wählt man nun eine Richtung, in der z.B. cω
o , die Geschwindigkeit des ordentlichen Strahls
2ω
der Grundwelle, mit cao , der Geschwindigkeit des außerordentlichen Strahls der Oberwelle
übereinstimmt, so bleiben Grund- und Oberwelle in Phase und der Kristall kann mit Dicken
der Größenordnung cm für die Frequenzverdopplung genutzt werden. Diese Technik wird als
6
Brechzahl− oder Phasenanpassung (index oder phase matching) bezeichnet und ist in Abb.5
erklärt, wo sich die Geschwindigkeitsflächen für ordentliche und außerordentliche Strahlen in
den Kristallrichtungen der Phasenanpassung schneiden.
Abb. 5: Geschwindigkeitsflächen für zueinander senkrecht polarisierte Lichtstrahlen in einem doppelbrechenden Medium. Die Schnittpunkte der Kugelflächen der ordentlichen (o) Strahlen und des Ovales
der außerordentlichen (ao) Strahlen legen die Richtungen fest, in denen die Geschwindigkeiten cω
o und
c2ω
der
beiden
Strahlen
übereinstimmen
(Phasenanpassung)
ao
Der Grad der Phasenanpassung kann durch Drehung des Kristalls oder Temperaturänderung
optimiert werden.
ˆ mit dem Quadrat der Feldstärke
Nach Formel 2.9 wächst die Feldstärke der Oberwelle E2ω
ˆ /Eˆω lassen sich somit durch FokusEˆω der Grundwelle an; hohe Umwandlungsgrade E2ω
sierung und Pulsen des Laserstrahles erzeugen. Mit Hilfe eines KTP-Kristalls kann z.B. die
gepulste infrarote (λ = 1064nm) Laserstrahlung eines Nd:YAG-Lasers bei einer Intensität von
4GW /m2 zu etwa 80% in grünes Licht mit 532nm Wellenlänge umgewandelt werden.
7
3 Vorbereitungsaufgaben
3.1 Kristallkohärenzlänge
Berechnen Sie für eine Erregerwelle der Wellenlänge λω = 1064nm und einen nichtlinearen
KTP-Kristall (Kalium-Titanyl-Phosphat) mit n2ω = 1,779 und nω = 1,738 die für Frequenzverdopplung gültige Kristallkohärenzlänge lK .
8
4 Aufbau des Lasers
Abb. 6: Diodengepumpter Festkörperlaser mit Frequnzverdoppelung.
4.1 Ausrichtung des Helium-Neon-Lasers
Entfernen Sie alle Bauteile bis auf den He/Ne-Laser und das Pinhole (LEOI-50-2) von der
optischen Bank. Der Strahl des He/Ne-Laser dient zur Ausrichtung der einzelnen Komponenten des diodengepumpten Festkörperlasers und der Frequenzverdopplung. Durch die sechs am
Laser befindlichen Schrauben lassen sich die Richtung und Höhe des Laserstrahls einstellen.
Durch Verschieben des Justierpinholes lässt sich der Laserstrahl entlang der optischen Achse
exakt ausrichten. Stellen Sie zum Schluss das Pinhole direkt vor den Laser.
4.2 Einstellung der Laserdiode (LEOI-50-7)
Die Laserdiode muss am anderen Ende der optischen Bank aufgebaut und die Schutzkappe
entfernt werden. Eine GRIN-Linse(GRadient-INdex) ist schon an der Laserdiode befestigt.
Richten Sie nun die Laserdiode so aus, dass der Strahl des He/Ne-Lasers auf die Mitte der
GRIN-Linse trifft und die Reflektion wieder durch das Pinhole tritt.
4.3 Messung der Laserdiodenleistungen
Stellen Sie den Messkopf (LEOI-50-8) des optischen Leistungsmessgeräts direkt hinter die
Laserdiode und schalten Sie das Messgerät an. Drehen Sie den Potentiometer am LaserdiodenController ganz herunter und schalten Sie den Controller an.
9
Das Messgerät ist auf die Wellenlänge eines He/Ne-Lasers von 632,8nm kalibriert. Um die
Lichtleistung des Diodenlasers mit der Wellenlänge 808nm zu messen, ist mit dem in der
Tabelle 1 aufgeführten Wert zu multiplizieren. Erhöhen Sie nun den Diodenstrom in 20mA
Schritten von 0 bis 400mA. Notieren Sie zu jeder Stufe die gemessene Lichtleistung.
Wellenlänge
Faktor
523nm
1,173
632,8nm
1,0
650nm
0,981
808nm
0,915
1064nm
7,286
Tab. 1: Faktoren zur Lichtleistungsmessung
4.4 Einstellung der Kristalle
Entfernen Sie den Messkopf des optischen Leistungsmessgeräts. Stellen Sie die Nd:YVO4 Halterung (LEOI-50-6) sehr nah an die Laserdiode (ca. 1mm) und richten Sie sie so aus, dass
der Laserstrahl durch den Kristall und die Reflektion wieder durch das Pinhole geht. Stellen
Sie die Halterung des KTPs (LEOI-50-5) so nah wie möglich dahinter und justieren Sie ihn
auf die gleiche Weise. Beim Justieren ist darauf zu achten, dass sich die Kristallhalterungen
nicht berühren.
4.5 Einstellung des Auskoppelspiegels (LEOI-50-4)
Bei der Platzierung des Auskoppelspiegels ist dessen Krümmungsradius von 50mm hinsichtlich der Resonatorlänge zu berücksichtigen. Des Weiteren muss der Auskoppelspiegel ebenfalls so ausgerichtet werden, dass der Strahl des He/Ne-Lasers wieder durch das Pinhole reflektiert wird. Nun kann der Justierlaser ausgeschaltet werden.
4.6 Inbetriebnahme des Lasers
Stellen Sie das Strom-Potentiometer des Laserdioden-Controllers auf Minimum und schalten Sie letzteren ein. Durch Erhöhung des Laserdiodenstroms auf über 80mA lässt sich an
Hand der Infrarot-Detektorkarte der Betrieb feststellen. Erhöhen Sie nun den Laserdiodenstrom (Vorsicht: Der Strom sollte 450mA nicht überschreiten.) bis der grüne Laserstrahl
erscheint.
Sollte sich kein grüner Laserstrahl einstellen lassen, müssen Sie die Ausrichtungen der Laserdiode und des KTP-Kristalls überprüfen und eventuell korrigieren. Variieren Sie die Orientierung des Auskoppelspiegels um ein möglichst starke Laserstrahlung zu erhalten.
10
4.7 IR-Sperrfilter (LEOI-50-3)
Der nun erzeugte Laserstrahl enthält noch einen Anteil der Laserdioden-Wellenlänge. Um
diesen zu blockieren muss hinter dem Auskoppelspiegel der IR-Sperrfilter positioniert werden.
4.8 Messung der Laserleistungen
Befestigen Sie den Messkopf (LEOI-50-8) des optischen Leistungsmessgeräts hinter dem IRSperrfilter und schalten Sie das Messgerät an. Stellen Sie nun die Drehscheibe des KTP’s so
ein das die maximale Leistung angezeigt wird.
Frage: 4.1 Warum ändert sich bei einer Drehung der KTP-Kristalls die gemessene Lichtleistung?
Drehen Sie den Laserdiodenstrom herunter. Erhöhen Sie nun den Strom wieder in 20mA
Schritten von 0 bis 400mA. Messen und notieren Sie hierbei wieder unter Berücksichtigung
der Tabelle 1 die jeweilige Lichtleistung.
Ermitteln Sie, zu jedem Messpunkt, wie groß das Verhältnis der Leistung des von Ihnen erstellten Lasers in Bezug zur Leistung der Laserdiode ist. Erstellen Sie in einem Tabellenkalkulationsprogramm ein Diagramm in dem Sie die Lichtleistungen der Laserdiode und des von
Ihnen erstellten, frequenzverdoppelten Nd : YVO4 -Lasers sowie den jeweiligen prozentualen
Leistungsanteil auftragen.
Frage: 4.2 Begründen Sie die jeweiligen Kurvenverläufe.
11