Ethan Frome

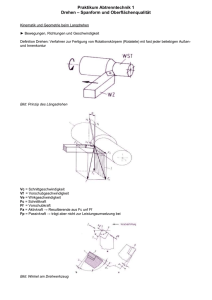
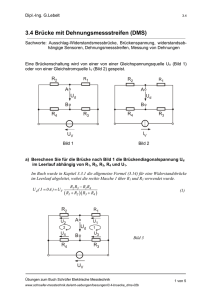
Technische Universität Dortmund
Institut für Spanende Fertigung
Prof. Dr.-Ing. Dirk Biermann
Wirtschaftsingenieurwissenschaftliches Labor (Diplom)
Wirtschaftswissenschaftliches Labor I (Bachelor)
Analysen und Kräftemessung im Zerspanprozess
Wintersemester 2010/11
Ansprechpartner: Dipl.-Ing. Ivan Iovkov, GB IV, Raum 214, Tel.: 0231 755 4860, E-Mail: [email protected]
Inhalt
1
2
3
4
5
6
Grundlagen
1.1
Schneidkeil, Geometrie
1.2
Komponenten der Zerspankraft
1.3
Geometrie der Zerspanung
1.4
Schnittkraft und spezifische Schnittkraft
1.5
Zerspanleistung
1.6
Spanarten
1.7
Spanformen
Verfahren der Schnittkraftmessung
2.1
Messung der Leistungsaufnahme (Taylor)
2.2
Schnittkraftmessung mit piezoelektrischen Kraftaufnehmern
2.3
Messung der Schnittkraft mit Dehnungsmessstreifen (DMS)
Versuchsaufbau
3.1
Messkette
3.2
Übertragungsfaktoren
Versuchsdurchführung
4.1
Erfassung der Schnittkraftkomponenten in Abhängigkeit von a p und f
4.2
Erfassung der Schnittkraftkomponenten in Abhängigkeit von vc
4.3
Werkstoff- und Werkstückdaten
Versuchsauswertung
5.1
Auswertung Versuchsreihe 4.1
5.2
Auswertung Versuchsreihe 4.2
5.3
Diskussion
Anhang
6.1
Technische Daten der Maschine
6.2
Messgeräte
1
1 Grundlagen
1.1
Schneidkeil, Geometrie
Grundprinzip der spanenden Formgebung ist die Wirkung des Schneidkeiles. Seine
charakteristischen Winkel sind der Spanwinkel  , der Keilwinkel  und der Freiwinkel .
Diese drei Winkel ergänzen sich zu 90° (Bild 1). Der Spanwinkel kann sowohl positiv als
auch negativ ausgeführt sein. Beim Spanen mit geometrisch bestimmter Schneide haben die
Winkel einen definierten Wert, bei Verfahren mit geometrisch unbestimmter Schneide nicht.
Beim Drehen liegt der Schneidkeil meist in Form einer Wendeschneidplatte vor (Bild 2).
Wendeschneidplatte
γ
β
Span
Span
f
Wendeschneidplatte
vc
vc
Werkstück
Draufsicht
f
α
Werkstück
Orthogonalansicht
Bild 1: Eingriffssituation der Wendeschneidplatte
Bild 2: Drehwendeschneidplatte im Werkzeughalter
2
1.2
Komponenten der Zerspankraft
Die Zerspankraft F greift am Schneidkeil des Werkzeuges an und lässt sich im Wesentlichen
in die drei Hauptkomponenten Fc (Schnittkraft), Fp (Passivkraft) und Ff (Vorschubkraft)
aufteilen (Bild 3).
Bild 3: Komponenten der Zerspankraft
1.3
Geometrie der Zerspanung
Die wichtigsten Zerspanungsgrößen sind die Schnittgrößen und die Spanungsgrößen. Die
Schnittgrößen müssen zur Spanabnahme unmittelbar oder mittelbar eingestellt werden. Es
sind:

Vorschub f

Schnittgeschwindigkeit vc

Schnitttiefe ap
Spanungsgrößen sind aus den Schnittgrößen abgeleitete Werte (Bild 4):

Einstellwinkel 

Spanungsdicke h = fsin 

Spanungsbreite b = ap /sin 
Der Spanungsquerschnitt A beschreibt die Fläche des noch nicht abgetrennten Spanes:
A= b  h = ap  f
3
f
f
vc
κ
A
ap
Bild 4: Geometrische Zusammenhänge beim Drehen
1.4
Schnittkraft und spezifische Schnittkraft
Zwischen Schnittkraft Fc und spezifischer Schnittkraft kc gilt die Beziehung:
Fc = A  kc
kc = Fc / A
Der Wert kc gibt die Schnittkraft bezogen auf den Spanungsquerschnitt an und ist abhängig
von dem zu zerspanenden Werkstoff, den Einstelldaten des Prozesses und der
Werkzeuggeometrie. Trägt man die kc-Werte über der Spanungsdicke h in doppelt
logarithmischem Maßstab in ein Diagramm ein, so ergibt sich annähernd eine Gerade
(Bild 5). Beim Spanungsquerschnitt A = 1 mm² und h = 1 mm ergibt sich der sogenannte kc 1.1
Wert.
kc = kc 1.1h-z
Fc = bkc 1.1h1-z
z = tan 
4
Bild 5: Spezifische Schnittkraft kc über der Spanungsdicke h1 für den Werkstoff Ck 60
1.5
Zerspanleistung
Die Zerspanleistung Pc berechnet sich nach:
Pc = Fcvc
1.6
Spanarten
Bei der Spanbildung findet in der Scherebene eine Umformung statt (Bild 6). Von dem
Umformverhalten des Werkstoffes hängt es ab, ob eine Werkstofftrennung auch in der
Scherebene erfolgt und wie stark sie ausgeprägt ist. Aufgrund dessen sind verschiedene
Spanarten zu unterscheiden (Bild 7), wobei allerdings auch Zwischenzustände auftreten
können.
5
Bild 6: Spanentstehung (nach König)
Bild 7: Spanarten
Der Spanablauf ist beim Fließspan gleichmäßig und ununterbrochen. Voraussetzung für die
Fließspanbildung ist ein ausreichendes Umformvermögen des Werkstoffes. Sie wird
begünstigt durch hohe Schnittgeschwindigkeit und große Spanwinkel. Scherspäne bilden sich,
wenn die Umformung in der Scherebene die Umformfähigkeit des Werkstoffes überschreitet.
Sie bestehen aus vollkommen getrennten Spanteilen, die wieder zusammenschweißen. Bei
Werkstoffen mit geringer Umformfähigkeit werden die Späne nicht mehr abgetrennt, sondern
aus der Oberfläche herausgerissen. Dieses Verhalten wird Reißspanbildung genannt.
1.7
Spanformen
Unter der Spanform versteht man die Form, mit der ein Span nach Abschluss des
Zerspanvorganges die Spanfläche des Werkzeuges verlässt. Man unterscheidet die in Bild 8
dargestellten Spanformen. Dabei sind Band- und Wirrspäne aufgrund ihrer Größe bzw. ihres
6
Platzbedarfes unerwünscht. Sie behindern die Maschinenbedienung, beschädigen Werkstück
und Werkzeug, beanspruchen viel Platz, können schlecht gehandhabt werden und erhöhen die
Unfallgefahr. Aus diesem Grunde werden zumindest Wendelspäne gefordert, wenn nicht
verfahrensbedingt noch kleinere Spanformen erforderlich sind. Dies kann der Fall sein, wenn
die Späne durch den Kühlschmierstoff transportiert werden müssen, wie z.B. beim
Tiefbohren.
Bild 8: Spanformen beim Drehen (nach Stahl-Eisen-Prüfblatt)
Da die Späne generell scharfkantig sind, sollte bei der Versuchsdurchführung geeignete
Kleidung und geschlossenes Schuhwerk getragen werden.
7
2 Verfahren der Schnittkraftmessung
2.1
Messung der Leistungsaufnahme (Taylor)
Die Messung der momentan aufgenommenen Leistung P des Spindelantriebes der
Werkzeugmaschine erlaubt die Bestimmung der Schnittkraft Fc. Bei bekanntem
Wirkungsgrad µ des Antriebes (Anteil der in Schnittleistung umgesetzten Leistung P) lässt
sich die Schnittkraft Fc in Abhängigkeit der Leistung P und der Schnittgeschwindigkeit vc
berechnen:
Fc = P  µ / vc
Dieses Verfahren wird heute zwar nicht mehr zur absoluten Kraftmessung eingesetzt, dient
aber als Maßstab für den Verschleißzustand von Zerspanwerkzeugen. Jede moderne
Werkzeugmaschine zeigt die aktuelle Leistungsaufnahme der Antriebe bzw. der Spindel an.
2.2
Schnittkraftmessung mit piezoelektrischen Kraftaufnehmern
Piezoelektrische Kraftaufnehmer nutzen den piezoelektrischen Effekt, um Kräfte, die auf
einen
piezoelektrischen
Kristall
wirken,
in
messbare
Spannungen
zu
wandeln.
Piezoelektrische Kristalle bestehen aus Ionen, die so im Kristallgitter angeordnet sind, dass
der Kristall unpolarisiert ist, d. h. die Ladungen der Ionen gleichmäßig verteilt sind, wenn er
nicht verformt wird. Wirkt eine Kraft F auf den Kristall, so wird er verformt. Dadurch
verlagern sich die Ionen im Kristall, woraus eine Ungleichverteilung der positiven gegenüber
den negativen Ionen entsteht. Diese Ungleichverteilung der Ladungen bewirkt eine
Polarisation des Kristalls, d. h. es ist zwischen der einen und der anderen Seite des Kristalls
eine Spannung messbar. Die Spannung ist proportional zur elastischen Verformung des
Kristalls, die wiederum proportional zur wirkenden Kraft ist. Diese Vorgänge sind vereinfacht
in Bild 9 dargestellt. Die Ladungsschwerpunkte der positiven und der negativen
Gesamtladung liegen bei einem piezoelektrischen Kristall ohne Krafteinwirkung aufeinander.
Unter Krafteinwirkung verformt sich der Kristall. Der positive Ladungsschwerpunkt wird
dadurch nach oben verschoben. Daraus resultiert eine Polarisation. In vergleichbarer Weise
reagiert ein geeigneter piezoelektrischer Kristall auch auf Zug- und Schubspannungen.
8
Bild 9: Links: Piezoelektrischer Kristall ohne Krafteinwirkung. Rechts: Kristall unter
Krafteinwirkung.
Die verwendete Kraftmessvorrichtung besitzt ein geeignetes piezoelektrisches Element für
jede Kraftrichtung. Zwei Elemente werden auf Schub und eines auf Druck belastet. Die
Elemente sind unter mechanischer Spannung eingebaut, um auch entlastende, also negative
Kräfte messen zu können.
Piezoelektrische Elemente eignen sich hervorragend für dynamische Untersuchungen, da sie
eine geringe Ansprechschwelle von 0,01 N besitzen, sowie eine hohe Eigenfrequenz von 1,5
bis 6 kHz und eine große Steifigkeit von 500 bis 5000 N/µm. Die hohe Steifigkeit bewirkt,
dass die wirkenden Kräfte nahezu weglos gemessen werden. Dies ist eine wesentliche
Voraussetzung für den Einsatz in Werkzeugmaschinen.
Die Kraftmesseinrichtung wird zur Messung der Zerspankraftkomponenten in der
Werkzeugmaschine zwischen Wendeschneidplattenhalter und Revolver eingebaut.
Ein Nachteil der Zerspankraftmessung mit piezoelektrischen Elementen liegt darin, dass die
von der Verformung erzeugten Überschussladungen auf der einen Seite des Kristalls langsam
über den Ladungsverstärker zur anderen Seite des Kristalls abfließen und so die Polarisation
verschwindet. Diesem Effekt wird durch elektronische Maßnahmen im Ladungsverstärker
entgegengewirkt, so dass er nicht zum Tragen kommt. Ein weiter Nachteil ist, dass die
piezoelektrischen Elemente sehr empfindlich auf Temperaturänderungen und hohe
Temperaturen reagieren. Eine konstante Temperatur des Sensors ist daher sicherzustellen. Bei
Zerspanversuchen kann dies die Kühlung der Kraftmesseinrichtung nötig machen.
9
2.3
Messung der Schnittkraft mit Dehnungsmessstreifen (DMS)
Eine weitere gebräuchliche Methode zur Kraftmessung ist die Anwendung von
Dehnungsmessstreifen (DMS). DMS bestehen aus einem mäanderförmig verlegten Leiter aus
Metallfolie oder Draht. Dieser Leiter wird auf die Oberfläche eines Bauteils geklebt. Eine auf
das Bauteil wirkende Kraft führt zu einer Verformung des Bauteils. Der DMS muss nun so
angebracht sein, dass die Verformung des Bauteils zu einer Dehnung des DMS führt.
Aufgrund der Dehnung des DMS verlängert sich der Leiter und sein Querschnitt verringert
sich gleichzeitig. Dadurch steigt der elektrische Widerstand des Leiters, der proportional zu
seiner Länge und invers proportional
zu seinem Querschnitt ist. Aus einer
Widerstandsänderung kann also die Dehnung ermittelt werden. Die Dehnung des DMS
entspricht der Dehnung des Bauteils und diese ist durch die mechanischen Eigenschaften des
Bauteils von der wirkenden Kraft abhängig.
Der momentane Widerstand des Leiters kann mithilfe einer Messschaltung, der sog.
Wheatston’schen Brücke, ermittelt werden. Diese Messschaltung und ein DMS sind in Bild
10 dargestellt.
Bild 10: Dehnungsmessstreifen und Wheatston’sche Brücke
Die Widerstände R2 und R3 der Schaltung sind gleich. RDMS ist der Widerstand des DMS. R4
ist ein Potentiometer, d. h. ein regelbarer Widerstand. Zwischen den Punkten 1 und 2 der
Schaltung wird eine Spannung angelegt. Über die beiden Pfade von 1 nach 2 fällt also die
gleiche Spannung ab. Die Spannung U zwischen den Punkten 3 und 4 ist somit vom
Verhältnis der Widerstände RDMS und R4 abhängig. Sind diese gleich, so ist die Spannung U
gleich null. Zur Messung von RDMS muss also R4 solange verändert werden, bis U = 0 ist.
Dann gilt R4 = RDMS.
10
DMS können beispielsweise auf den Schaft des Werkzeughalters geklebt werden und messen
so die unter der Belastung auftretende Verformung. Die erwünschte und üblicherweise
vorhandene sehr steife Ausführung einer Werkzeugmaschine und dem Werkzeughalter steht
hier jedoch dem Messprinzip entgegen und beeinflusst die Messgenauigkeit in negativer
Weise. Daher ist dieses Verfahren zur Messung der Zerspankraft weniger geeignet als die
Verwendung von piezoelektrischen Kraftaufnehmern.
Der Vorteil der Kraftmessung mit DMS liegt darin, dass sowohl statische als auch
dynamische Kräfte erfasst werden können. Zudem ist die Anwendung von DMS relativ
einfach und kostengünstig.
11
3 Versuchsaufbau
3.1
Messkette
Der piezoelektrische Kraftaufnehmer (das Dynamometer) erzeugt eine Ladung Q, die
proportional zur wirkenden Kraft F ist. Der Ladungsverstärker ermittelt aus dieser Ladung die
wirkende Kraft F und gibt eine zur Kraft proportionale Spannung aus. Diese wird durch die
Messkarte des Rechners wiederum in die wirkende Kraft F umgerechnet und angezeigt.
Dieser Vorgang wird mit einer Abtastrate von 1 kHz durchgeführt, dass bedeutet, dass 1000
Mal pro Sekunde für jede der drei Kraftrichtungen die wirkende Kraft vom Rechner
abgetastet und aufgezeichnet wird (Bild 11).
Bild 11: Messkette
3.2
Übertragungs- und Kalibrierfaktoren
Für die Einstellung des Ladungsverstärkers wird für jede der drei Kraftrichtungen ein
Kalibrierfaktor benötigt, den der Hersteller des Kraftaufnehmers angibt (Bild 12). Diese
Faktoren werden durch Kennlinien dargestellt, die eingemessen wurden.
Bild 12: Kennlinie der Kraftaufnehmer
12
Der Ladungsverstärker wandelt die Ladung Q in eine proportionale Spannung U. Dazu wird
am Verstärker der Kalibrierfaktor eingestellt, der festlegt, welche Ladung Q in Picocoulomb
(pC = 10-12C) durch eine Kraft F in Newton (N) im Dynamometer erzeugt und an den
Verstärker weitergeleitet wird. Des Weiteren wird am Verstärker ein Übertragungsfaktor
eingestellt, der festlegt, welche Spannung U am Ausgang des Verstärkers angelegt wird, wenn
eine Kraft von 1 N gemessen wird. Dieser Übertragungsfaktor kann in gewissen Grenzen frei
gewählt werden, um eine möglichst hohe Auflösung zu erzielen.
13
4 Versuchsdurchführung
4.1
Erfassung der Schnittkraftkomponenten in Abhängigkeit von ap, f und vc
Die Schnittkraft, die Vorschubkraft und die Passivkraft sind im ersten Versuchsteil für
verschiedene Schnitttiefen a1 ... a6 und für verschiedene Vorschübe f1 ... f6 zu messen. Die
Drehzahl n bleibt dabei konstant.
Ausgegangen wird von dem Parametersatz vc = 200 m/min, f = 0,15 mm und ap = 0,4 mm.
Die gemittelten Kräfte im stationären Bereich werden in die folgenden Tabellen eingetragen.
Abgelesen werden können die gemittelten Werte direkt aus der entsprechenden Auswertung
der Messsoftware LabView (National Instruments). Dabei wird ein Zeitfenster gewählt, in
dem das Kraftsignal einen nahezu stationären Wert erreicht. Aufgrund der Datenmenge kann
dieser Mittelwert bei manueller Auswertung nur sehr mühsam bestimmt werden.
Neben Angabe des Mittelwertes soll in der Auswertung noch die Standardabweichung der
Mittelwerte angegeben werden, wobei diese zu bewerten sind.
vc = 200 m/min, f = 0,15 mm und ap = var
Schnitttiefenvariation
ap1 = 0,05
ap2=0,1
ap3=0,2
ap4=0,4
ap5=0,75
ap6=1
f3 = 0,1
f4 = 0,2
f5 = 0,3
f6 = 0,4
ap in mm
Fc in N/ Stabw.
Ff in N / Stabw.
Fp in N / Stabw.
vc = 200 m/min, f = var und ap = 0,4 mm
Vorschubvariation
f1 =0,025
f2 = 0,05
f in mm
Fc in N / Stabw.
Ff in N / Stabw.
Fp in N / Stabw.
Die Schnittkraft, die Vorschubkraft und die Passivkraft sind im zweiten Versuchsteil für
verschiedene Schnittgeschwindigkeiten vc1... vc6 zu messen. Die Schnitttiefe ap und der
Vorschub f bleiben konstant.
14
Angegeben werden sollen wieder die Mittelwerte und die zugehörigen Werte der
Standardabweichung. Außerdem soll jeweils die für die Schnittgeschwindigkeit vci (i=1...6)
notwendige Drehzahl ni berechnet werden.
vc = var, f = 0,15 mm und ap = 0,4 mm
Schnittgeschwindigkeitsvariation (m/min)
vc1 = 150
vc2= 200
vc3= 225
vc4= 250
vc5= 275
vc6= 300
Berechn. Drehzahl n
Fc in N / Stabw.
Ff in N / Stabw.
Fp in N / Stabw.
4.2
Werkstoff- und Werkstückdaten
Werkstoffbezeichnung:
nach DIN 17 200:
Härte HB weichgeglüht:
Seco Werkstoffgruppe:
Durchmesser des Rohteiles
Durchmesser des Fertigteiles:
Werkzeugdaten:
Spanwinkel 0:
Keilwinkel 0:
Freiwinkel 0:
Einstellwinkel :
15
5 Versuchsauswertung
5.1
Auswertung Versuchsreihe 4.1
Zur Auswertung der Versuchsreihe sind folgende Diagramme zu zeichnen:
Diagramm I, Bearbeitungskräfte unter Variation der Schnitttiefe:
Fc = f(ap)
Fp = f(ap)
Ff = f(ap)
Diagramme II und III, Spezifische Schnittkraft in Abhängigkeit des Vorschubes und der
Schnitttiefe:
kc = f(f)
für f1 ... f6
kc = f(ap)
für ap1 ... ap6
Diagramm IV, Spezifische Schnittkraft in Abhängigkeit der Spanungsdicke h:
kc = f(h)
doppelt logarithmische Darstellung
Berechnen Sie kc1.1!
5.2
Auswertung Versuchsreihe 4.2
Zur Auswertung der Versuchsreihe sind folgende Diagramme zu zeichnen:
Diagramm V, Bearbeitungskräfte in Abhängigkeit der Schnittgeschwindigkeit:
Fc = f(vc)
Fp = f(vc)
Ff = f(vc)
Berechnen Sie die jeweilige mittlere Zerspanleistung.
5.3
Diskussion
Die Versuchsergebnisse sind in einem Kurzbericht von maximal 8 Seiten (Inhalt! Deckblatt
o.ä. ausgenommen) zu diskutieren. Mögliche Fehler und deren Quellen oder ungewöhnliche
Messergebnisse sind einzuordnen und zu begründen. Dazu gehören auch die Kurvenverläufe
der Diagramme I-V. Bitte beachten Sie, dass sich die Ergebnisse der Versuche von
Ergebnissen, die in der üblichen Literatur dargestellt werden, abgrenzen können. Auch hierfür
sollten mögliche Ursachen angegeben werden. Abschließend ist ein Vortrag in Form einer
Power-Point-Präsentation über die Versuchsergebnisse und –durchführung zu halten. Der
Vortrag sollte nicht länger als 20 min dauern. Jede Präsentation, die länger als 22 min dauert,
16
wird nach Ablauf der 22. Minute unterbrochen und alles nicht vorgetragene zählt als nicht
erbrachte Leistung.
Die Folien der Präsentation werden als Anlage mit dem Kurzbericht abgegeben. Beides ist
mindestens drei Werktage vor dem Vortrag bei einem der Betreuer einzureichen.
Die Präsentation findet innerhalb von zwei Monaten nach der Versuchsdurchführung statt.
Der Termin wird direkt nach dem Versuch oder maximal einen Tag später vereinbart.
Am Tag der Versuchsdurchführung wird vor Beginn des Versuches das nötige Wissen zum
Versuch abgefragt. Hierbei wird von allen Teilnehmern erwartet, dass sie sich angemessen
auf den Versuch vorbereitet haben und somit alle Fragen beantworten können. Sollte sich eine
Gruppe bzw. ein Teilnehmer als ungenügend vorbereitet herausstellen, kann diese
Gruppe/Person den Versuch frühestens im nächsten Jahr wiederholen. Tipp: Bitte beachten
Sie insbesondere die Unterschiede der Abbildungen 1 und 4 und das hierfür zur Verfügung
gestellte Video (Download siehe Skriptdownload)!
Für Fragen, die im Vorfeld auftreten, steht der Betreuer Ivan Iovkov (GB IV, Raum 214,
Tel.: 0231 755 4860, Email: [email protected]) gerne zur Verfügung.
Kritik an der Versuchsplanung und Vorschläge zur Verbesserung sind erwünscht!
17
6 Anhang
6.1
Technische Daten der Maschine
Maschine:
Monforts RNC 602
60°-Schrägbett-Drehmaschine
Drehzahlbereich: 28 ... 4000 1/min
Max. Drehlänge 600 mm
Drehdurchmesser über Schlitten: 210 mm
Drehdurchmesser über Bett: 360 mm
Antriebsleistung 30 kW
Bild 15: Drehmaschine Monforts (Quelle: ISF)
6.2
Messgeräte
Dynamomenter:___________________________________
Ladungsverstärker: ________________________________
Messkarte: National Instruments _____________________
Messprogramm: LabView (NI)
Abtastrate:___________ Hz
18