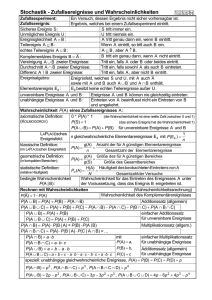
2.2 Ereignisse und deren Wahrscheinlichkeit

2.2 Ereignisse und deren Wahrscheinlichkeit
Literatur: [Papula Bd. 3, Kap. II.2 und II.3], [Benning, Kap. 3], [Bronstein et
al., Kap. 13.2.1]
Def 1 [Benning] Ein Zufallsexperiment ist ein beliebig oft wiederholbarer, nach
einer bestimmten Vorschrift auszuführender Vorgang, dessen Ergebnis zufallsbedingt ist, d.h. im voraus nicht eindeutig bestimmt werden kann. Ein möglicher
Ausgang eines Zufallsexperiments heißt Ereignis, wobei man Elementarereignisse und zusammengesetzte Ereignisse unterscheidet.
Elementarereignisse sind die einzelnen nicht mehr zerlegbaren und sich gegenseitig ausschließenden Möglichkeiten für den Ausgang eines Zufallsexperiments.
Sie werden mit ω1 , ω2 , . . . , ωn bezeichnet. Deren Menge Ω = {ω1 , ω2 , . . . , ωn }
bildet den Ereignisraum.
Jede Teilmenge von A ⊂ Ω beschreibt ein zusammengesetztes Ereignis. Das
Ereignis A ist eingetreten, wenn das Ergebnis des Zufallsexperiments ein Element von A ist.
Bsp 2
• Würfeln mit einem Würfel ist ein Zufallsexperiment. Es sind 6 verschiedene Elementarereignisse möglich, Ω = {1, 2, 3, 4, 5, 6}. Die Ereignisse
Würfeln einer geraden Zahl, A = {2, 4, 6}, und Würfeln einer durch 3
teilbaren Zahl, B = {3, 6}, sind zusammengesetzte Ereignisse.
• Beim Würfeln mit einem roten und einem blauen Würfel sind 36 verschiedene Elementarereignisse möglich. Das Ereignis Pasch besteht aus 6
Elementarereignissen.
• Beim Werfen einer Münze enthält der Ereignisraum nur die Elementarereignisse Kopf und Zahl.
Bem 3 Sowohl die leere Menge ∅ als auch die Menge Ω sind definitionsgemäß
Teilmengen des Ereignisraums Ω und somit Ereignisse. Dabei symbolisiert ∅
ein Ereignis, das nie eintreten kann, das unmögliche Ereignis . Die Menge Ω
symbolisiert ein Ereignis, das immer eintritt, das sichere Ereignis .
Beim Würfeln ist das Ereignis Zahl größer gleich 1 und kleiner gleich 6 das
sichere Ereignis und Zahl kleiner 1 oder größer 6 das unmögliche Ereignis.
Da Ereignisse Teilmengen des Ereignisraums Ω sind, können diese auch mit
den Mengenoperationen verknüpft werden. Man erhält neue Ereignisse.
Def 4 Die Vereinigung A∪B der Ereignisse A und B kennzeichnet ein Ereignis,
bei dem wenigstens eines der Ereignisse A oder B eintritt.
Unter dem Durchschnitt A ∩ B der Ereignisse A und B versteht man das
Ereignis, das eintritt, wenn sowohl A als auch B eintreten.
Das zu A komplementäre Ereignis A tritt genau dann ein, wenn A nicht
eintritt, d.h., A = Ω \ A.
Disjunkte Ereignisse (sich gegenseitig ausschließende Ereignisse) A und B
können nicht gemeinsam auftreten, A ∩ B = ∅.
2.2 – 1
Bsp 5 Beim Würfeln betrachten wir die Ereignisse
A = {1, 3, 5}
(Würfeln einer ungeraden Zahl),
B = {2, 4, 6}
(Würfeln einer geraden Zahl).
Dann gilt:
• B ist das zu A komplementäre Ereignis.
• A ∪ B ist das sichere Ereignis.
• A ∩ B ist das unmögliche Ereignis.
Def 6 (Klassische Wahrscheinlichkeit nach Laplace) Sind bei einem Zufallsexperiment mit endlichem Ereignisraum alle Elementarereignisse gleich wahrscheinlich, spricht man von einem Laplace-Experiment.
Bei einem Laplace-Experiment ist die Wahrscheinlichkeit P (A) für das Eintreten des Ereignisses A gleich dem Verhältnis aus der Anzahl der für das Ereignis günstigen Fälle (Anzahl der Elementarereignisse in A) und der Anzahl
aller möglichen Fälle (Anzahl der Elementarereignisse im Ereignisraum Ω),
P (A) =
Anzahl der günstigen Fälle
.
Anzahl der möglichen Fälle
Bsp 7 Beim Würfeln mit einem Würfel hat jedes Elementarereignis die Wahrscheinlichkeit 16 . Die Wahrscheinlichkeit, eine gerade Zahl zu würfeln, beträgt
1
3
6 = 2.
Bsp 8 Beim Würfeln mit zwei (unterscheidbaren) Würfeln hat jedes Elemen1
tarereignis die Wahrscheinlichkeit 36
. Die Wahrscheinlichkeit, Pasch zu würfeln,
6
beträgt 36
= 16 .
Diese Wahrscheinlichkeit ergibt sich natürlich auch bei zwei nicht unterscheidbaren Würfeln. Wir müssen diese künstlich unterscheiden, damit das Ereignis
Würfeln einer Eins und einer Zwei als zwei Elementarereignisse (1, 2) und (2, 1)
gezählt werden kann. Nur so haben alle Elementarereignisse die gleiche Wahr1
scheinlichkeit wie (1, 1), nämlich 36
.
Ü 9 Wie groß ist die Wahrscheinlichkeit, beim Würfeln mit zwei Würfeln die
Augensumme 9 zu erzielen?
Ü 10 Jemand würfelt mit drei Würfeln und bietet Ihnen an, Ihren Einsatz zu
verdoppeln, wenn eine der zehn möglichen Augenzahlen 3, 4, 5, 6, 7, 14, 15,
16, 17 oder 18 gewürfelt wird, während Ihr Einsatz verloren geht, wenn eine
der sechs Augenzahlen 8, 9, 10, 11, 12 oder 13 gewürfelt wird. Würden Sie
mitspielen?
Ü 11 Wie groß ist die Wahrscheinlichkeit beim Lotto 6 aus 49 sechs bzw. fünf
richtige Zahlen zu tippen?
2.2 – 2
Satz 12 Die Wahrscheinlichkeit nach Laplace genügt den folgenden Eigenschaften.
1. P ist nichtnegativ und normiert, 0 ≤ P (A) ≤ 1.
2. Für das sichere Ereignis Ω gilt P (Ω) = 1.
3. Für disjunkte Ereignisse A1 , A2 , A3 , . . . gilt
P (A1 ∪ A2 ∪ A3 ∪ . . .) = P (A1 ) + P (A2 ) + P (A3 ) + . . . .
Bem 13 Es gibt auch eine statistische Definition der Wahrscheinlichkeit nach
R. von Mises über die Betrachtung der Häufigkeit bei unendlichem Wiederholen
des Zufallsexperiment, was praktisch aber nicht möglich ist.
In der modernen Wahrscheinlichkeitstheorie wird der Begriff Wahrscheinlichkeit als Grundbegiff aufgefasst, der den Axiomen von A. N. Kolmogoroff genügt.
Dies sind gerade die Eigenschaften aus Satz 12.
Folgerung 14
1. Für das zum Ereignis A komplementäre Ereignis A gilt P (A) = 1 − P (A).
2. Für das unmögliche Ereignis ∅ gilt P (∅) = 0.
3. Für zwei beliebige Ereignisse A und B gilt
P (A ∪ B) = P (A) + P (B) − P (A ∩ B).
Beweis A und A sind disjunkte Ereignisse. Folglich gilt
P (A) + P (A) = P (A ∪ A) = P (Ω) = 1.
Damit ist die erste Eigenschaft bewiesen. Die zweite folgt unmittelbar aus der
ersten.
Für die dritte Eigenshaft stellen wir A, B und A ∪ B als Vereinigung von
disjunkten Ereignissen dar,
A = (A \ B) ∪ (A ∩ B),
B = (B \ A) ∪ (A ∩ B),
A ∪ B = (A \ B) ∪ (B \ A) ∪ (A ∩ B).
Folglich gilt
P (A) = P (A \ B) + P (A ∩ B),
P (B) = P (B \ A) + P (A ∩ B),
P (A ∪ B) = P (A \ B) + P (B \ A) + P (A ∩ B)
= P (A) − P (A ∩ B) + P (B) − P (A ∩ B) + P (A ∩ B).
Damit ist alles gezeigt.
q.e.d.
2.2 – 3
Def 15 (bedingte Wahrscheinlichkeit) Die Wahrscheinlichkeit für das Eintreten des Ereignisses B unter der Bedingung oder Voraussetzung, dass das Ereignis A bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit und wird durch
das Symbol P (B|A) gekennzeichnet, lies Wahrscheinlichkeit für B unter der
”
Bedingung A“. Sie wird durch die Gleichung
P (B|A) =
P (A ∩ B)
P (A)
definiert.
Bsp 16 In einer Urne befinden sich drei weiße und drei schwarze Kugeln. Die
Wahrscheinlichkeit, bei der ersten Ziehung eine weiße Kugel zu ziehen, beträgt
3
6 = 0.5. Ist in der ersten Ziehung tatsächlich eine weiße Kugel gezogen worden,
beträgt die Wahrscheinlichkeit, bei der zweiten Ziehung eine weiße Kugel zu
ziehen, nur noch 52 = 0.4, während sich die Wahrscheinlichkeit, in der ersten
Ziehung eine schwarze Kugel zu ziehen, sich auf 53 = 0.6 erhöht hat.
Bsp 17 Auf einem Parkplatz stehen 8 Autos, drei rote VW, ein blauer VW,
drei blaue Opel und ein roter Opel. Nach einem Sturm wurde ein Auto von
einem herab gefallenen Ast beschädigt.
Die Wahrscheinlichkeit, dass ein VW beschädigt wurde, ist gleich der Wahrscheinlichkeit, dass ein Opel beschödigt wurde, nämlich 12 .
Jetzt wird bekannt, dass ein blaues Auto beschädigt wurde. Damit sind die
Wahrscheinlichkeiten für ein beschädigtes Auto sofort völlig anders verteilt:
3
1
4 für den Opel und 4 für VW.
Zur formalen Lösung definieren wir die beiden Ereignisse A und B.
A Es wurde ein blaues Auto getroffen.
B Es wurde ein Opel getroffen.
Es ist P (B) = 12 , P (A ∩ B) =
3
8
und damit
P (B|A) =
P (A ∩ B)
3/8
3
=
= .
P (B)
1/2
4
Bsp 18 (Ziegenproblem) Der Gewinner eines Spiels findet seinen Gewinn hinter einer von 3 Türen. Hinter einer Tür befindet sich der Hauptgewinn, hinter
den anderen beiden je eine Ziege. Nachdem er eine Tür ausgewählt hat, öffnet
der Spielleiter eine der anderen beiden Türen; dabei kommt eine Ziege zum
Vorschein. Danach wird der Kandidat gefragt, ob bei seiner Tür bleiben oder
sich umentscheiden möchte. Wie würden Sie sich entscheiden?
Bezeichnen wir die ausgewählte Tür mit A, die vom Spielleiter geöffnete Tür
mit B und die verbliebene Tür mit C. Offenbar gilt
1
,
3
P (Hauptgewinn hinter Tür B | Hauptgewinn nicht hinter Tür B) = 0.
P (Hauptgewinn hinter Tür A) =
Folglich gilt
P (Hauptgewinn hinter Tür C | Hauptgewinn nicht hinter Tür B) =
Man sollte sich also umentscheiden.
2.2 – 4
2
.
3
Satz 19 (Multiplikationssatz) Die Wahrscheinlichkeit für das gleichzeitige
Eintreten zweier Ereignisse A und B ist
P (A ∩ B) = P (A) · P (B|A) = P (B) · P (A|B).
Beweis Die Behauptung folgt aus der Definition der bedingten Wahrscheinlichkeit.
q.e.d.
Bsp 20 In einer Urne befinden sich drei weiße und drei schwarze Kugeln. Wie
groß ist die Wahrscheinlichkeit, dass bei zwei Ziehungen (ohne Zurücklegen)
zwei weiße Kugeln gezogen werden?
Wir betrachten dazu die beiden zufälligen Ereignisse
A Bei der 1. Ziehung wird eine weiße Kugel gezogen.
B Bei der 2. Ziehung wird eine weiße Kugel gezogen.
Wir haben oben bereits ausgerechnet, dass P (A) = 12 und P (B|A) = 25 ist.
Nach unserem Satz gilt P (A ∩ B) = P (A) · P (B|A) = 12 · 25 = 51 .
Zur Probe überlegen wir uns, dass es 62 = 30 Möglichkeiten gibt, zwei
Kugeln aus 6 auszuwählen. Dabei sind 6 günstige Fälle.
Def 21 Zwei Ereignisse A und B sind unabhängig, wenn P (B|A) = P (B) und
P (A|B) = P (A) gilt.
Folgerung 22 Aus dem Multiplikationssatz folgt für unabhängige Ereignisse
P (A ∩ B) = P (A) · P (B).
2.2 – 5