Sinus, Cosinus und Tangens am Einheitskreis - Nachhilfe

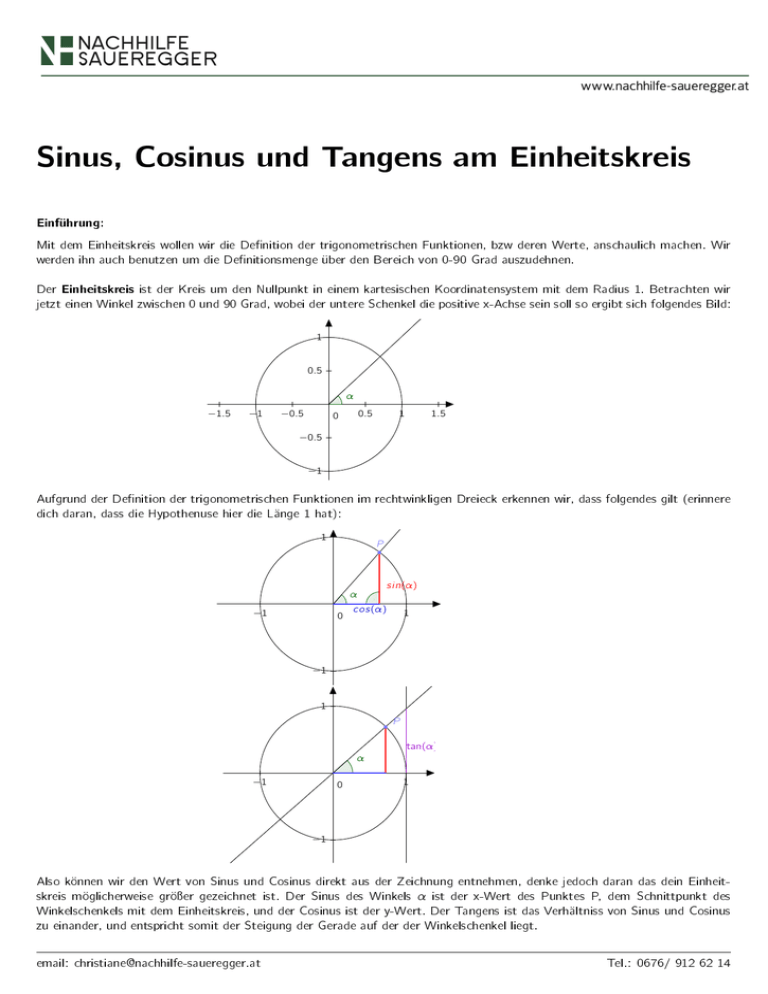
Sinus, Cosinus und Tangens am Einheitskreis
Einführung:
Mit dem Einheitskreis wollen wir die Denition der trigonometrischen Funktionen, bzw deren Werte, anschaulich machen. Wir
werden ihn auch benutzen um die Denitionsmenge über den Bereich von 0-90 Grad auszudehnen.
Der Einheitskreis ist der Kreis um den Nullpunkt in einem kartesischen Koordinatensystem mit dem Radius 1. Betrachten wir
jetzt einen Winkel zwischen 0 und 90 Grad, wobei der untere Schenkel die positive x-Achse sein soll so ergibt sich folgendes Bild:
1
0.5
α
−1.5
−1
−0.5
0.5
0
1
1.5
−0.5
−1
Aufgrund der Denition der trigonometrischen Funktionen im rechtwinkligen Dreieck erkennen wir, dass folgendes gilt (erinnere
dich daran, dass die Hypothenuse hier die Länge 1 hat):
1
P
sin(α)
α
−1
0
cos(α)
1
−1
1
P
tan(α)
α
−1
0
1
−1
Also können wir den Wert von Sinus und Cosinus direkt aus der Zeichnung entnehmen, denke jedoch daran das dein Einheitskreis möglicherweise gröÿer gezeichnet ist. Der Sinus des Winkels α ist der x-Wert des Punktes P, dem Schnittpunkt des
Winkelschenkels mit dem Einheitskreis, und der Cosinus ist der y-Wert. Der Tangens ist das Verhältniss von Sinus und Cosinus
zu einander, und entspricht somit der Steigung der Gerade auf der der Winkelschenkel liegt.
email: [email protected]
Tel.: 0676/ 912 62 14
Erweiterung auf 360◦ :
Den Sinus und Cosinus für Winkeln gröÿer als 90◦ , denieren wir genauso wie oben, als x- bzw. y-Wert des Punktes P. So ergibt
sich für die einzelnen Quadranten folgendes Bild:
1
1
1
P
α
sin(α)
−1 cos(α) 0
cos(α)
1
−1
sin(α)
α
0
α
−1
1
0
cos(α)
1
sin(α)
P
P
−1
−1
−1
Aus den Bildern können wir nun einige Eigenschaften ablesen. So ergibt sich für die Vorzeichen von Sinus und Cosinus folgende
Tabelle:
sin(α)
cos(α)
tan(α)
I. Quadrant
+
+
+
Folgende Formeln lassen sich herleiten:
II. Quadrant
+
-
IV. Quadrant
+
si n2 (α) + cos 2 (α) = 1
tan(α) =
email: [email protected]
III. Quadrant
+
-
si n(α)
cos(α)
Tel.: 0676/ 912 62 14