Kapitel 6: Graphen

Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6. Graphen
• viele praktische (Optimierungs-)Probleme sind als
graphentheoretische Probleme formulierbar
• z.B. in Produktionsplanung, Personaleinsatzplanung, . . .
6.1 Grundlagen
• gerichteter, ungerichteter und gewichteter Graph
158
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Gerichteter Graph
Definition: gerichteter Graph G = (V , E) mit:
V = {v0 , . . . , vn−1 }
Knotenmenge
E ⊂V ×V
Kantenmenge (im folgenden: m =| E |)
• Graphen werden meist graphisch dargestellt
Beispiel:
G1 = ({v0 , v1 , v2 , v3 }, {(v0 , v2 ), (v1 , v2 ), (v2 , v1 ), (v2 , v3 )})
v0
v1
v2
v3
159
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Ungerichteter Graph
Definition: ungerichteter Graph G = (V , E) mit:
V = {v0 , . . . , vn−1 }
Knotenmenge
E ⊂ {{v , v 0 } | v , v 0 ∈ V }
Kantenmenge
Beispiel:
G2 = ({v0 , v1 , v2 , v3 }, {{v0 , v2 }, {v1 , v2 }, {v2 , v3 }})
v0
v1
v2
v3
• im folgenden werden gerichtete Graphen betrachtet,
sofern nicht explizit anders hervorgehoben
160
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Gewichteter Graph
Definition: gewichteter Graph G = (V , E, β) mit:
Knotenmenge V
Kantenmenge E
β : E−→IR
(Kanten-)Gewichtsfunktion
Beispiel:
G3 = ({v0 , v1 , v2 , v3 }, {(v0 , v2 ), (v1 , v2 ), (v2 , v1 ), (v2 , v3 )}, β)
mit β(v0 , v2 ) = 2, β(v1 , v2 ) = 5, β(v2 , v1 ) = 3, β(v2 , v3 ) = 2
v0
2
v2
v1
5
3
2
v3
161
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.2 Datenstrukturen für Graphen
6.2.1 Adjazenzmatrix
sei G = (V , E) ein Graph
Definition: Adjazenzmatrix AG ist n × n-Matrix mit

 1, falls (vi , vj ) ∈ E und 0 ≤ i, j < n (bzw. {vi , vj } ∈ E)
ai,j =

0, sonst
Beispiel:
v0

v1
AG1
G1 :
v2
v3

0
0
1
0

 0
= 
 0

0
0
1
1
0
0
0

0 

1 

0
• Platzbedarf: O(n2 )
162
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.2.2 Adjazenzlisten
• Array (oder sonstige Kollektion) von Knoten
• für jeden Knoten: Liste mit Verweisen auf Nachfolgeknoten
Beispiel:
0
v0
v2
2
3
-
-
G1 :
1
v1
v3
2
-
2
1
-
3
• Kantengewichte leicht ergänzbar
• Platzbedarf: O(n + m)
163
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.2.3 Distanzmatrix
sei G = (V , E, β) ein gewichteter Graph
Definition: Distanzmatrix DG ist n × n-Matrix mit

 β(vi , vj ), falls (vi , vj ) ∈ E und 0 ≤ i, j < n (bzw. {vi , vj } ∈ E)
di,j =
 ∞,
sonst
Beispiel:
v0
2
G3 :

v1
5
v2
DG3
3
2
v3
∞


 ∞ ∞ 5 ∞

= 
 ∞ 3 ∞ 2

∞ ∞ ∞ ∞






∞ ∞
2
• Platzbedarf: O(n2 )
164
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.3 Transitive Hülle
• gegeben: G = (V , E)
• gesucht: (reflexive,) transitive Hülle G∗ = (V , E ∗ ) mit:
• (v , v ) ∈ E ∗
0
∀v ∈ V
∗
• (v , v ) ∈ E , (v 0 , v 00 ) ∈ E ⇒ (v , v 00 ) ∈ E ∗
∀v , v 0 , v 00 ∈ V
• sonst keine Kanten in E ∗
Beispiel:
G1∗ =
G1 =
(V , E):
v0
v1
v0
v1
v2
v3
v2
v3
(V , E ∗ ):
165
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Transitive Hülle (Warshall-Algorithmus)
• gegeben: Adjazenzmatrix AG von G = (V , E)
public static void huelle(byte[][] A){
int n = A.length;
for(int i=0; i<n; i++)
A[i][i] = 1;
for(int j=0; j<n; j++)
for(int i=0; i<n; i++)
// Schleifenreihenfolge
// wichtig!
if (A[i][j] == 1)
for(int k=0; k<n; k++)
if (A[j][k] == 1)
A[i][k] = 1;}
• Iteration j berücksichtigt alle Verbindungen mit Zwischenstationen ≤ j
rth
• Aufwand: tW
(n, m) ∈ O(n2 + | E ∗ | ·n))
166
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.4 Traversierung von Graphen
6.4.1 Tiefensuche
• an jedem Knoten:
• zuerst die Nachfolger rekursiv betrachten
• dann die “Geschwister”
Beispiel:
G4:
v0
v1
v4
v2
v3
v5
• Durchlaufreihenfolge: v0 , v2 , v1 , v4 , v3 , v5
dfs (n, m) ∈ O(n + m) (bei Adjazenzlisten)
• Aufwand: tW
167
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.4.2 Breitensuche
• alle Knoten mit Abstand i vom Ausgangsknoten
werden vor denen mit Abstand i + 1 besucht (i = 0, 1, 2, . . .)
• hierzu: Knotenqueue (FIFO)
Beispiel:
G4:
v0
v1
v4
v2
v3
v5
• Durchlaufreihenfolge: v0 , v2 , v1 , v3 , v4 , v5
bfs (n, m) ∈ O(n + m) (bei Adjazenzlisten)
• Aufwand: tW
168
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.5 Kürzeste Wege
6.5.1 Kürzeste Wege von einem Ausgangsknoten
• sei G = (V , E, β) mit β : E−→IR+
Algorithmus von Dijkstra (grober Pseudocode)
drei Knotenmengen: F (fertig), R (Rand), U (unerreicht)
anfangs:
F = {v0 }; R = Nachbarn(v0 ); U = V − F − R
bis F == V
(*) bestimme v ∈ R mit d(v0 , v ) ≤ d(v0 , v 0 ) ∀v 0 ∈ R
F = F ∪ {v }
R = R ∪ (Nachbarn(v ) − F ) − {v }
U =U −R
169
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Aufwand des Algorithmus von Dijkstra
• abhängig von der Implementierung der Knotenauswahl (*):
1) durchlaufe alle Knoten: → Aufwand O(n2 ) (Original)
2) mit Knoten-Heap: → Aufwand O(m · log n)
3) mit Knoten-Fibonacci-Heap (s. Ottmann/Widmayer):
Aufwand O(m + n · log n)
170
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Beispiel: Algorithmus von Dijkstra
v1
5
2
3
2
v2
0
v0
6
v2
0
v0
6
v1
3
v2
2
3
1
3
v2
0
v0
v1
5
2
2
6
3
v2
2
1
v4
2
v3
2
5
3
4
5
1
v4
2
v3
3
6
4
5
1
v4
2
v3
7
4
3
2
v4
v1
5
2
5
2
v3
2
5
2
v4
6
v0
0
1
2
v1
3
2
6
v3
2
5
2
2
6
v0
0
3
4
6
171
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.5.2 Alle Paare kürzester Wege
Ansatz 1: n-mal Dijkstra-Algorithmus
• Aufwand: O(n3 ) bzw. O(n · m · log n) (mit Heap)
Ansatz 2: Floyd-Algorithmus
• Variante des Warshall-Algorithmus basierend auf Distanzmatrix
• . . . A[i][k] = min(A[i][k], A[i][j]+A[j][k]) . . .
• Aufwand: O(n2 + | E ∗ | ·n)
172
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Ansatz 3: (+,min)-Multiplikationen
geg.: Distanzmatrix D
M = D;
for(int i=0; i <= log2 n; i++)
M = M ⊕ M;
wobei ⊕: (+,min)-Matrixmultiplikation, d.h. min statt +, + statt ·
• Aufwand: O(n3 · log n)
• verbesserbar auf: O(n2.81 · log n) mit Strassen-Verfahren
173
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.6 Minimaler Spannender Baum
• gegeben: ungerichteter, gewichteter Graph G = (V , E, β)
• gesucht: Baum B = (V , E 0 , β 0 ) mit E 0 ⊂ E, β 0 = β |E 0 und
P
β(e) minimal
e∈E 0
Algorithmus von Kruskal (Pseudocode)
E0 = ∅
while B noch kein Baum do
wähle e ∈ E − E 0 mit kleinstem β(e)
und so dass B = (V , E 0 ∪ {e}) “kreisfrei”
E 0 = E 0 ∪ {e}
• Aufwand: O(m · log n) mit “union-find-Struktur”
(s. z.B. Ottmann/Widmayer)
174
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Beispiel: Algorithmus von Kruskal
6
v0
v1
2
v4
2
3
2
6
v0
v3
v1
2
1
3
3
v2
2
6
v0
1
v4
2
v3
v1
3
1
2
2
2
v4
2
3
v2
v1
2
2
v2
6
v0
1
2
v3
3
2
v4
2
3
v2
2
v3
3
175
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Algorithmus von Jarník/Prim/Dijkstra
• analog zu Dijkstra-Algorithmus (s.o)
• jedoch wird für jeden Randknoten der Abstand zum fertigen Baum
vermerkt (nicht zum Anfangsknoten)
Beispiel:
6
v0
v1
6
2
v4
2
3
v2
2
6
v0
3
v3
v1
v4
2
3
v2
2
2
6
v0
1
6
v0
1
v1
2
1
2
2
3
2
v3
v1
2
v2
2
v4
2
3
3
2
v3
3
3
1
2
2
v4
2
3
v2
v1
2
2
2
6
v0
1
2
v3
3
1
2
v4
2
3
v2
2
v3
3
• Aufwand: O(m + n log n) (mit Fibonacci-Heap)
176
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
6.7 Maximaler Fluss
• gegeben: gewichteter Graph G = (V , E, β) mit
β : E−→IR+
Kantenkapazität
q∈V
Quelle
s∈V
Senke
• gesucht: maximaler Fluss f : E−→IR+ von q nach s
d.h.
max (
P
f :E−→IR+ (q,v )∈E
f (q, v ) −
(v 0 ,q)∈E
* f (e) ≤ β(e) ∀e ∈ E
P
P
*
f (v 0 , v )−
(v 0 ,v )∈E
f (v 0 , q)) mit:
P
Kapazitätsrestriktion
00
f (v , v ) = 0 ∀v ∈ V −{q, s} Flusserhaltung
(v ,v 00 )∈E
177
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Beispiel: Fluss
3/ 2
v0
4/ 4
v1
1/ 0 3/ 2
q
4/ 3
v2
3/ 3
s
1/ 1
3/ 2
1/ 1
v3
5/ 4
Definition:
• ein zunehmender Weg w von q nach s mit Kapazität k ist eine
• Kantenfolge ( v00 , v10 ), (v10 , v20 ), . . . , (vr0−1 , vr0 ) mit
|{z}
|{z}
=s
=q
0
0
0
• f (vi0 , vi+1
) + k ≤ β(vi0 , vi+1
), falls (vi0 , vi+1
)∈E
•
0
f (vi+1
, vi0 )
− k ≥ 0,
(für i = 0, . . . r − 1)
falls
0
(vi+1
, vi0 )
oder
∈E
178
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Beispiel: Flusserhöhung
4/ 4
3/ 2
v0
1/ 0 3/ 2
q
4/ 3
v2
v1
s
1/ 1
3/ 2
1/ 1
v3
4/ 4
3/ 3
5/ 4
3/ 1
v0
1/ 0 3/ 3
q
4/ 4
v2
v1
3/ 3
s
1/ 1
3/ 3
1/ 1
v3
5/ 5
• Fluss f 0 nach Addition des zunehmenden Weges w: (für i = 0, . . . r − 1)
0
0
f 0 (vi0 , vi+1
) := f (vi0 , vi+1
) + k,
0
falls (vi0 , vi+1
)∈E
0
0
und f (vi0 , vi+1
) + k ≤ β(vi0 , vi+1
)
0
0
f 0 (vi+1
, vi0 ) := f (vi+1
, vi0 ) − k ,
sonst
179
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Algorithmus von Ford/Fulkerson
für alle e ∈ E: f (e) = 0;
while ∃ zunehmenden Weg w von q nach s do
sei k die (max.) Kapazität von w
erhöhe f entlang w um k
• zur Implementierung: speichere f (e) für jede Kante e
• bei naiver Wahl von w ist weder die Termination noch die Korrektheit
garantiert
Aufwand im schlechtesten Fall:
• abhängig vom Vorgehen bei der Bestimmung des zunehmenden Weges
1) wenn w mit maximaler Kapazität: O(m · log βmax )
2) wenn w mit minimaler Kantenanzahl: O(n · m2 )
(Algorithmus von Edmonds/Karp (Breitensuche))
180
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Andere Maximal-Fluss-Algorithmen
• Algorithmus von Dinic: O(n2 · m) verbessert Alg. v. Edmonds/Karp;
alle kürzesten Wege werden gleichzeitig berücksichtigt
• Algorithmus von Karsanow/Tarjan: O(n3 )
• Algorithmus von Sleator/Tarjan: O(n · m · log n)
• Details siehe Ottmann/Widmayer
Bemerkungen:
• maximaler Fluss entspricht “minimalem Schnitt”
• ein Fluss f ist maximal, wenn es keinen zunehmenden Weg gibt
181
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
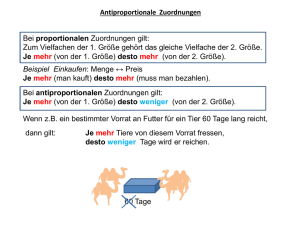
5.8 Zuordnungen
Definition: (Zuordnung)
• sei G = (V , E) ein Graph; E 0 ⊂ E heißt Zuordnung (Matching), wenn
∀(v , v 0 ) ∈ E 0 6 ∃v 00 ∈ V − {v , v 0 }
{(v 00 , v ), (v 00 , v 0 ), (v , v 00 ), (v 0 , v 00 )} ∩ E 0 6= ∅
182
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Bipartite Graphen
Definition: (bipartiter Graph)
• sei G = (V , E) ein Graph mit V = V1 ∪ V2 und V1 ∩ V2 = ∅
• G heißt bipartit, wenn E ⊂ V1 × V2 ∪ V2 ∩ V1
Bestimmung einer maximalen Zuordnung
• die Bestimmung einer (bzgl. | E 0 |) maximalen Zuordnung in einem
bipartiten Graphen lässt sich auf das Maximal-Fluss-Problem
zurückführen
• hierzu werden Knoten q und s ergänzt und q mit allen Knoten von V1
und s mit allen Knoten von V2 verbunden
• das Gewicht jeder Kante ist 1
183
Grundlagen Datenstrukturen Transitive Hülle Traversierung Kürzeste Wege Spannender Baum Max. Fluss Zuordnungen
Beispiel: Bestimmung einer maximalen Zuordnung
1
Adam
1
Anna
1
1
1
Bernd
1
Christian
q
1
Birgit
1
1
s
Chantal
1
1
1
1
Dieter
1
Doris
1
zunehmende Wege:
1) q→A1 →A2 →s
2) q→B1 →C2 →s
3) q→D1 →D2 →s
4) q→C1 →C2 ← B1 →A2 ← A1 →B2 →q
184