Übungsblatt 2
Werbung

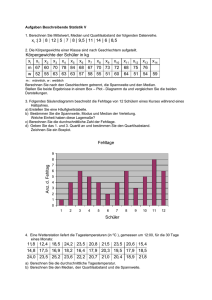
MAT 183: Stochastik für die Naturwissenschaften SS 2007 Übungsblatt 2 Themen: Masszahlen und Darstellung von Versuchsergebnissen, Streuungsmasse, Wahrscheinlichkeitsbegriffe Abgabetermin: Mittwoch, 4. April, bzw. Freitag, 13. April, bei der Übungsleiterin oder beim Übungsleiter in der jeweiligen Übungsstunde. Statistische Masszahlen und Darstellung von Versuchsergebnissen Aufgabe 7 (◦). In einer Schule wurde die Länge (in m) des Schulwegs aller Schüler und Schülerinnen ermittelt. Es ergab sich folgende Klasseneinteilung: Länge [0, 500] (500, 1000] (1000, 1500] (1500, 2000] (2000, 2500] Anzahl 30 35 20 10 5 a) Zeichnen Sie das Histogramm (absolute Häufigkeiten). b) Bestimmen Sie das arithmetische Mittel und den Median des Merkmals Länge des Schulwegs. Lösung. a) b) Es wurden 100 Schülerinnen und Schüler in die Studie einbezogen. Um das arithmetische Mittel x̄ des Merkmals Länge des Schulwegs zu bestimmen, betrachten wir anstelle der Klassen den jeweiligen mittleren Wert. So erhalten wir x̄ = 1 30 · 250 m + 35 · 750 m + · · · + 5 · 2250 m = 875 m. 100 Version vom 20. März 2007, 9:56 Uhr Seite 1 MAT 183: Stochastik für die Naturwissenschaften SS 2007 Um den Median dieses stetigen Merkmals zu bestimmen, bemerken wir, dass 30 Personen der Klasse [0, 500] und 35 Personen der Klasse [500, 1000] zugehören. Von den letzteren teilen wir 20 nach links und 15 nach rechts ein. Mit anderen Worten, wir teilen die Intervallbreite 500 m im Verhältnis 20 : 15 in die Längen 285.71 m und 214.29 m. Der Median x̃ beträgt also x̃ = 500 m + 285.71 m = 785.71 m. Aufgabe 8 (5 Punkte). Bestimmen Sie a) das arithmetische Mittel, b) den Median, c) das 25%-Quartil und e) das 75%-Quartil der folgenden Daten: 6, 17, 26, 7, 13, 25, 9, 21, 10, 15, 19, 7. Zeichnen Sie einen Boxplot dieser Daten. Hinweis. Unter dem 25%-Quartil wollen wir denjenigen (in unserem Fall eindeutigen) Datenwert q25% verstehen, bei dem 25% der Daten kleiner sind als q25% . Genauso ist das 75%-Quartil q75% dadurch definiert (wiederum eindeutig in unserem Fall), dass 75% der Datenwerte kleiner sind als q75% (vgl. dazu Storrer, Band 2, S. 31/32). Dies sind in gewissem Sinne ad hoc-Definitionen. Boxplots werden unterschiedlich definiert. Wir verwenden die Definition aus der Vorlesung, bzw. aus Storrer, Band 2, S. 32. Aufgabe 9 (3 Punkte). In der Schule gibt es ganze und halbe Noten zwischen 1 und 6. Sechs Schülerinnen erhielten in einer Prüfung die Noten 2.5, 3.5, 4.5, 5, 5.5, 6. Die Note der siebenten Schülerin ist nicht bekannt. a) Welches ist die kleinst- bzw. die grösstmögliche Durchschnittsnote? b) Welche Möglichkeiten gibt es für den Median der sieben Noten? Aufgabe 10. (4 Punkte) Am Wochenende vom 1./2. März 2003 wurden in den verschiedenen Runden der Schweizer Fussball-Nationalliga die folgenden Resultate erzielt: Finalrunde Xamax-Basel GC-Young Boys Thun-Wil Servette-FCZ 2:1 1:2 0:2 0:1 Auf-/Abstiegsrunde A/B Delémont-Lugano Aarau-Sion Kriens-Vaduz St. Gallen-Luzern 1:1 3:1 3:2 versch. Platzierungsrunde B Yverdon-Schaffhausen Bellinzona-Wohlen Winterthur-Lausanne Concordia-Baden versch. 2:2 0:0 3:1 Das zu untersuchende Merkmal ist die Anzahl Tore pro Match. Verschobene Spiele sind nicht zu berücksichtigen. a) Zeichnen Sie das Stabdiagramm. b) Stellen Sie die Summenhäufigkeitsverteilung graphisch dar. Aufgabe 11 (3 Punkte). Berechnen Sie Durchschnitt, Median und Modus der Daten aus der vorhergehenden Aufgabe. Aufgabe 12 (5 Punkte). An einer Prüfung mit 40 Teilnehmern konnten maximal 10 Punkte erzielt werden, die sich wie folgt verteilten: Anzahl Punkte 0 1 2 3 4 5 6 7 8 9 10 Anzahl KandidatInnen 0 0 3 2 3 4 6 8 6 5 3 Version vom 20. März 2007, 9:56 Uhr Seite 2 MAT 183: Stochastik für die Naturwissenschaften SS 2007 a) Zeichnen Sie das zugehörige Stabdiagramm. b) Zeichnen Sie den Graphen der Summenhäufigkeitsverteilung. c) Berechnen Sie das arithmetische Mittel und den Median des Merkmals Punktzahl. Aufgabe 13 (5 Punkte). Die Messung der Körperlänge (auf 0.5 cm genau) von 24 achtjährigen Mädchen ergab folgende Werte (in cm): 134, 125, 129, 136, 133.5, 128.5, 130.5, 136, 126.5, 128.5, 129, 124, 125, 134.5, 133, 135, 134, 122.5, 130, 127, 128, 131, 120.5, 131 a) Zeichnen Sie das Histogramm für eine Klassenbreite von 2 cm, beginnend mit der Klasse (120.25, 122.25]. b) Zeichnen Sie das Histogramm für eine Klassenbreite von 4 cm, beginnend mit der Klasse (120.25, 124.25]. c) Stellen Sie die Summenhäufigkeitsverteilung bezüglich der Klasseneinteilung von a) grafisch dar. Aufgabe 14 (3 Punkte). Eine Untersuchung über das monatliche Einkommen einer Gruppe von 50 Personen ergab folgende Daten: Einkommen <3000 3000-5000 5000-7000 7000-9000 >9000 Anzahl 9 20 9 9 3 Berechnen Sie den Median. Könnten Sie auch den Durchschnitt berechnen? Aufgabe 15 (4 Punkte). Ein (idealisiertes) Histogramm eines stetigen Merkmals ist gegeben durch die Funktion 3x + 3 für −1 ≤ x ≤ 1, f (x) := 6 für 1 < x < 2, −x + 8 für 2 ≤ x ≤ 8. Zeichnen Sie die zugehörige Figur und berechnen Sie den Median x̃. Aufgabe 16 (3 Punkte). Eine idealisierte Summenhäufigkeitsverteilung ist im Intervall [1, 4] durch die Funktion (x − 1)2 F (x) := 3 gegeben. Skizzieren Sie den Graphen von F . Berechnen Sie den Median x̃ dieser Verteilung, und zeichnen Sie ihn in die Figur ein. Streuungsmasse Aufgabe 17 (2 Punkte). Berechnen Sie Variationsbreite und Interdezilbereich, sowie die empirische Varianz und Standardabweichung von folgenden Daten: 87, 135, 207, 305, 369, 352, 76, 391, 167, 300, 212. Aufgabe 18 (4 Punkte). An einer Prüfung erzielten die 50 Teilnehmer und Teilnehmerinnen die folgenden Noten: Note 1 2 3 4 5 6 Anzahl 1 5 10 17 11 6 Version vom 20. März 2007, 9:56 Uhr Seite 3 MAT 183: Stochastik für die Naturwissenschaften SS 2007 Berechnen Sie den Interdezilbereich, die Variationsbreite, die empirische Varianz und die Standardabweichung. Aufgabe 19 (3 Punkte). 100 Ostereier wurden in Gewichtsklassen eingeteilt: Gewicht in g (46, 50] (50, 54] (54, 58] (58, 62] (62, 66] (66, 70] Anzahl 6 17 33 25 14 5 Berechnen Sie die empirische Varianz und die Standardabweichung. Verschiedene anschauliche Wahrscheinlichkeitsbegriffe Aufgabe 20 (◦). Ein Stäbchen der Länge 10 cm wird an einer zufällig ausgewählten Stelle x (mit 0 ≤ x ≤ 10) markiert und dort in zwei Teile getrennt. Mit welcher Wahrscheinlichkeit unterscheiden sich die beiden Teile um höchstens 1 cm? Welcher Wahrscheinlichkeitsbegriff ist hier am Platz? Aufgabe 21 (3 Punkte). Ein Würfel ist verfälscht. Ein Versuch mit 500 Würfen ergab folgende Häufigkeiten für die Augenzahlen: Augenzahl 1 2 3 4 5 6 Anzahl 30 60 100 110 100 100 Mit welcher Wahrscheinlichkeit würfeln Sie a) keine 3, b) eine gerade Zahl, c) eine Primzahl? Welche Art der Wahrscheinlichkeit haben Sie verwendet? Aufgabe 22 (4 Punkte). An einer Mathematikprüfung konnten maximal 60 Punkte erreicht werden. Dabei erzielten die 24 Teilnehmerinne und Teilnehmer folgende Punktzahlen: 41, 15, 23, 39, 53, 27, 45, 37, 37, 42, 28, 15, 37, 56, 30, 25, 40, 56, 39, 48, 60, 23, 24, 4. Für 30-35 Punkte gibt es eine Vier, für 53 oder mehr Punkte eine Sechs. Mit welcher Wahrscheinlichkeit hat eine beliebig ausgewählte Person a) eine Sechs, b) eine genügende Note, c) eine Punktzahl unter dem Durchschnitt, d) eine Punktzahl über dem Median? (Überrascht das Resultat von d)?) Mit welchem Wahrscheinlichkeitsbegriff arbeiten Sie hier? Aufgabe 23 (4 Punkte). Wir würfeln gleichzeitig mit zwei (fairen) Würfeln. Wie gross ist die Wahrscheinlichkeit dafür, dass a) die beiden Augenzahlen sich genau um 2 unterscheiden, b) das Produkt der beiden Augenzahlen zwischen 10 und 13 liegt? c) Aus den Augenzahlen (als Ziffern betrachtet) wird eine zweistellige Zahl gebildet: Wenn sie verschieden sind, die grössere vor die kleinere gesetzt. (Wenn beide gleich sind, kommt es auf die Reihenfolge natürlich nicht an.) Mit welcher Wahrscheinlichkeit ist die so gebildete Zahl durch 4 teilbar? Welcher Wahrscheinlichkeitsbegriff wurde verwendet? Aufgabe 24 (5 Punkte). Auf einer Ebene sind parallele Geraden gezeichnet, die abwechslungsweise den Abstand 1 cm und 7 cm haben. Eine Münze vom Durchmesser 2 cm wird zufällig auf die Ebene geworfen. Wie gross ist die Wahrscheinlichkeit dafür, dass sie auf a) zwei, b) genau einer, c) keiner Geraden liegt? Welchen Wahrscheinlichkeitsbegriff brauchen Sie? Version vom 20. März 2007, 9:56 Uhr Seite 4