VI. Funktionentheorie Eine komplexe Zahl z = x + iy ist gegeben

VI. Funktionentheorie
Eine komplexe Zahl z = x + iy ist gegeben durch
zwei reelle Zahlen: Realteil x und Imaginärteil y.
Eine komplexe Funktion f = f (z) hat daher die
Form f (z) = u(z) + iv(z) oder
f (z) = u(x, y) + iv(x, y)
mit reellen Funktionen u = u(x, y) und v = v(x, y).
Für die partiellen Ableitungen gilt
∂x z = 1 ,
∂y z = i,
also (Kettenregel) fx = f ′(z) und fy = f ′(z)i. y
f ′(z) = fx = ux + ivx
f ′(z) = −ify = −i(uy + ivy ) = vy − iuy
Koeffizientenvergleich liefert die Cauchy-Riemannschen Differentialgleichungen:
ux = v y ,
uy = −vx
Die Ableitung f ′(z) wird wie im Reellen definiert:
f (z + h) − f (z)
f ′(z) = lim
.
h→0
h
Da die komplexe Zahl h von jeder Richtung aus
gegen 0 streben kann, bedeutet die Existenz dieses
Grenzwerts f ′(z) jedoch eine starke Einschränkung
für die Funktion f . Man kann nämlich zeigen:
Satz 14. Ist eine komplexe Funktion f = f (z)
einmal differenzierbar, so ist sie auch beliebig oft
differenzierbar.
Mit diesen differenzierbaren komplexen Funktionen,
die nach Satz 14 sogar beliebig oft differenzierbar
(und, weil stetig, auch beliebig oft integrierbar) sind,
befaßt sich die “Funktionentheorie”. Man nennt solche Funktionen auch holomorph (=formvollendet).
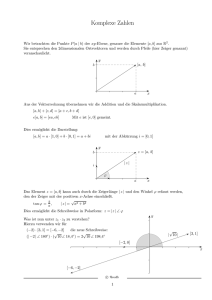
Komplexe Zahlen stellt man nach Gauß in der
Ebene dar (Gaußsche Zahlenebene), indem man
den Imaginärteil auf der y-Achse abträgt:
x + iy = reiϕ
iy
i
r
ϕ
1
x
Die komplexe Exponentialfunktion überführt Polarkoordinaten (r = eu > 0, ϕ = v) in kartesische
Koordinaten (x = r cos ϕ, y = r sin ϕ):
eu+iv = eueiv = eu(cos v + i sin v)
2
Für z = reiϕ wird der Abstand r von 0 auch mit
|z| bezeichnet (Betrag von z). Der Winkel ϕ heißt
auch Argument arg z von z.
Satz 15. Bei der Multiplikation komplexer Zahlen multiplizieren sich die Beträge und addieren
sich die Winkel:
reiϕ · seiψ = (rs)ei(ϕ+ψ).
Da 2π den Vollwinkel darstellt, gilt e2πi = 1 und
entsprechend
e2πni = 1
für alle n ∈ Z. Die Zahlen eiϕ mit ϕ ∈ R befinden
sich auf dem Einheitskreis:
|eiϕ| = 1.
Wegen der Eulerschen Formel
eiϕ = cos ϕ + i sin ϕ
cos ϕ
hat also der Vektor sin ϕ ∈ R2 die Länge 1:
cos2 ϕ + sin2 ϕ = 1.
Nach Satz 15 besteht die Multiplikation mit einer
komplexen Zahl z = reiϕ in einer Drehstreckung:
Streckung um r, Drehung um den Winkel ϕ.
3
Aus der Eulerschen Formel ergibt sich
cos ϕ =
eiϕ +e−iϕ
2
sin ϕ =
,
eiϕ −e−iϕ
2i
Mit diesen Formeln kann man sin z und cos z auch
für komplexe Zahlen z (statt ϕ) berechnen.
Wegen eu+iv = eueiv bildet die e-Funktion den
Streifen
v
2πi
0 6 v < 2π
u
0
der Breite 2π bijektiv auf C r {0} ab. Die Umkehrfunktion (Logarithmus) hat daher diesen Streifen als
Wertebereich:
ln(reiϕ) = ln r + iϕ
Dies folgt aus der Formel
ln(ab) = ln a + ln b
welche zur Gleichung ea+b = eaeb äquivalent ist.
Auch die allgemeine Potenzfunktion läßt sich aus
der e-Funktion herleiten:
ab = eb ln a
4