Voransicht

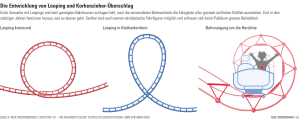
18. Die Physik einer Loopingbahn untersuchen
1 von 16
Spreepark Berlin – die Physik einer Loopingbahn untersuchen
Matthias Borchardt, Bonn
I/B
Warum sind Loopings in Achterbahnen niemals
kreisförmig konstruiert? Welche Beschleunigungen
wirken auf den Fahrgast, wenn er einen Looping
durchfährt? Wann fällt man aus einem Looping
heraus?
Foto: dpa/picture-alliance
Fragen wie diese beantworten Ihre Schüler selbstständig. Eine Computersimulation gestattet darüber
hinaus einen besonders anschaulichen und schüleraktivierenden Zugang zu diesem spannenden
Thema.
T
H
C
I
S
N
A
R
O
V
Eine Loopingbahn im Spreepark Berlin
Schwindelfrei auf der Achterbahn –
der Computer macht’s möglich!
Der Beitrag im Überblick
Klasse:
10
Inhalt:
Dauer:
3–5 Stunden
– Energieumwandlungen bei einer Achterbahnfahrt

– Berechnung der Geschwindigkeit
v und

Beschleunigung a in verschiedenen
Punkten der Bahn mithilfe des Energiesatzes und mithilfe eines Kräfteansatzes
Ihr Plus:
Eine Computersimulation als Arbeitsund Kontrollwerkzeug
Die Schüler erkennen, dass man Achterbahnen unter physikalischen Gesichtspunkten konstruieren muss, um die
Gesundheit des Fahrgastes nicht zu
gefährden.
– Einluss der Reibung
– Vergleich von Kreis- und Klothoidenloopings
27 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
2 von 16
Fachliche und didaktisch-methodische Hinweise
Ein Thema mit Motivationspotenzial und Kontextorientierung
I/B
Auch wenn Ihre Schüler niemals in einer Achterbahn saßen und die viel beschriebene Ausschüttung von Adrenalin beim Durchfahren eines Loopings nicht am eigenen Leib erfahren haben –
von dem Thema Achterbahnfahren geht eine so starke Faszination aus, dass es die Schüler in
der Regel mit großem Interesse aufnehmen.
Die Beschäftigung mit Loopingbahnen lohnt sich aber nicht nur aus diesem Grund. Das Thema
stellt auch einen kontextbildenden Baustein dar, weil es auf natürliche Weise lehrplanimmanente Unterrichtsinhalte wie Energieerhaltung, Energieumwandlung, Kreisbewegungen, Trägheitssatz, Kräftebilanz und Zwangsbewegungen miteinander verbindet. Damit setzen Sie eine
wesentliche Forderung des Lehrplans um, nämlich, die verschiedenen Inhalte des Physikunterrichts in Kontexten zu unterrichten, die aus der Lebenswelt der Schüler stammen.
Eine Computersimulation als dynamisches Werkzeug
Eine Fahrt durch eine Loopingbahn ist aus physikalischer Sicht komplex. Daher können Sie mit
Ihren Schülern konkrete Rechnungen nur an ausgezeichneten Stellen der Bahn durchführen.
Beispielsweise lassen sich die Geschwindigkeiten und Beschleunigungen im höchsten und
tiefsten Punkt des Loopings berechnen, wie auch die Mindestgeschwindigkeit, die erforderlich
ist, um nicht aus dem Looping zu fallen.
T
H
C
Solche punktuellen Herleitungen und Rechnungen vermitteln Ihren Schülern aber einen eher
statischen Eindruck von der Physik einer Loopingbahn. Um die Dynamik der Gesamtbewegung
ins Blickfeld zu rücken, steht Ihnen auf der CD-ROM 27 eine Computersimulation zur Verfügung
(auch unter http://www.mabo-physik.de/looping.html). Mit diesem kleinen Computerprogramm
können Ihre Schüler einen Wagen (Kugel) auf einer Startrampe aus verschiedenen Höhen
losrollen lassen. Der Wagen läuft dann in einen Looping, dessen Form kreisförmig, klothoidenförmig oder eine Mischung aus beiden ist. Während der Fahrt werden die Geschwindigkeit
und die Beschleunigung, die der Fahrgast senkrecht zur Bahn spürt (die Normalbeschleunigung bzw. Kraft, mit der er in den Sitz gedrückt wird), in zwei Diagrammen aufgezeichnet.
Diese eignen sich hervorragend, um beispielsweise die Frage zu klären, warum man auf Jahrmärkten niemals Kreisloopings indet. Ebenso können Ihre Schüler die Absturzproblematik bei
zu geringer Geschwindigkeit diskutieren und das Fahrverhalten bei eingeschalteter Reibung
ablesen. Darüber hinaus stellt die Computersimulation ein Kontrollwerkzeug dar, mit dem Ihre
Schüler eigene Berechnungen direkt überprüfen können.
I
S
N
A
R
O
V
Ein kleinschrittiger Zugang zur Physik einer Loopingbahn
Das Material thematisiert die Physik einer Loopingbahn recht kleinschrittig und ist daher
umfangreich. Geben Sie Ihren Schülern für die Bearbeitung genügend Zeit. Planen Sie etwa
drei bis vier Schulstunden ein. Lassen Sie Ihre Schüler die Aufgaben in Partnerarbeit lösen.
Jede Lerngruppe gibt nach Abschluss eines Arbeitsblattes ihre Lösungen ab, die von Ihnen
bewertet werden.
Obwohl die Arbeitsblätter die Schüler langsam an die Lösung der Aufgaben heranführen, kann
es sein, dass Hilfestellungen notwendig sind. Für einige Aufgaben haben wir daher gestaffelte
Lösungshilfen (Tippkarten M 6) erstellt, die Sie bei Bedarf ausgeben.
26 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
4 von 16
Materialübersicht
I/B
 V = Vorbereitungszeit
SV = Schülerversuch
Ab = Arbeitsblatt/Informationsblatt
 D = Durchführungszeit
LV = Lehrerversuch
Fo = Folie
M1
Ab
Die Physik einer Loopingbahn – Einstieg ins Thema
 V: 5 min
 D: 10 min
M2
Ab
Die mathematische Form einer Loopingbahn
 V: 5 min
 D: 15 min
M3
Ab
 V: 5 min
 D: 135 min
Ideen zur Loopingbahn – Bewegungsgrößen berechnen
rComputersimulation: Looping.exe
rInternetzugang
rTaschenrechner
T
H
C
rTippkarten (M 6)
M4
Info-Blatt
 V: 5 min
Rückenschmerzen und Schleudertrauma garantiert – der Flip-FlapLooping von 1895
I
S
N
 D: 25 min
M5
Ab
Wann fällt man raus? – Die Mindestgeschwindigkeit angeben
A
R
O
 V: 5 min
 D: 90 min
M6
V
Tippkarten
Die Erläuterungen und Lösungen zu den Materialien inden Sie ab Seite 12.
26 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
M1
5 von 16
Die Physik einer Loopingbahn – Einstieg ins Thema
Axel steht vor dem großen Looping im Spreepark
Berlin. Ihn bewegen folgende Fragen:
– Welche Geschwindigkeiten und welche Beschleunigungen nimmt ein Mensch wahr, wenn er eine
Loopingbahn durchfährt?
I/B
– Warum sind Loopings in Achterbahnen niemals
kreisförmig gebaut?
– Wann fällt man aus der Loopingbahn heraus?
In dieser Unterrichtseinheit gehen Sie diesen Fragen
nach. Mithilfe einer Computersimulation erhalten Sie
außerdem spannende Einblicke in die Physik von
Loopingbahnen.
T
H
C
I
S
N
A
R
O
Modellannahmen
Foto: dpa/picture-alliance
Haben Sie sich ähnliche Fragen auch schon einmal
gestellt? Oder ging es Ihnen nur um den AdrenalinKick bei der Fahrt auf der Achterbahn?
Berlin: Der Mega-Loop im Vergnügungs- und
Freizeitpark im Plänterwald ist eine der größten Loopingbahnen Europas.
Die Physik einer Achterbahn ist schwierig. Zur Vereinfachung gehen wir von folgenden Modellannahmen aus, die die Berechnungen leichter machen:
V
1. In den meisten Aufgaben berücksichtigen Sie die Reibung (Luft- und Rollreibung) nicht.
2. Sie sehen die in der Loopingbahn bewegte Masse als Massepunkt an.
Der Umstand, dass es sich eigentlich um eine Wagenkette handelt, die durch den Looping rast,
führt zwar zu interessanten physikalischen Folgerungen, entfernt Sie aber von der eigentlichen
Intention dieses Beitrages, nämlich die grundlegenden Aspekte verschiedener Loopingbahnen
zu begreifen.
Modell einer Loopingbahn
27 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
6 von 16
M2
Die mathematische Form einer Loopingbahn
Wir beschreiben die einzelnen Abschnitte der Achterbahn durch mathematische Kurven.
Die Achterbahn – in einzelne Abschnitte zerlegt
I/B
Die Fahrt beginnt auf einer Rampe. Dort gewinnt der Wagen zunächst an Geschwindigkeit. Die
Rampe hat eine maximale Höhe von 40 m und besteht aus folgenden Abschnitten:
Abschnitt A stellt eine schiefe Ebene mit einem
Neigungswinkel von 45° dar.
Die Abschnitte B und C sind Klothoidenausschnitte,
die so aneinandergefügt wurden, dass ein glatter
Übergang von einem Kurvenstück zum anderen
gewährleistet ist. Einen solchen Übergang bezeichnet
man auch als Scheitelklothoide. Was eine Klothoide
ist, werden Sie im Material M 3 lernen.
Abschnitt D ist ein 10 m langes waagrechtes Geradenstück.
T
H
C
Nachdem der Wagen diese vier Abschnitte passiert hat, fährt er durch einen Looping. Drei
verschiedene Loopingarten stehen Ihnen zur Auswahl – alle haben eine Höhe von 20 m.
I
S
N
Kreislooping
Dieser Looping hat einen Radius von 10 m und ist exakt
kreisförmig.
A
R
O
V
Klothoiden-Kreis-Looping
Dieser Looping besteht aus zwei symmetrischen
Klothoidenabschnitten, auf die ein Kreissegment
(Kreisradius 8 m) gesetzt wurde.
Klothoidenlooping
Hier wurden zwei symmetrische Klothoidenäste im
Scheitelpunkt nahtlos aneinandergesetzt.
26 RAAbits Physik Mai 2012
20 m
18. Die Physik einer Loopingbahn untersuchen
M3
7 von 16
Ideen zur Loopingbahn – Bewegungsgrößen berechnen
Mithilfe dieses Arbeitsblattes erkunden Sie schrittweise, was physikalisch hinter einer Loopingbahn steckt. Ihr Lehrer steht Ihnen beratend zur Verfügung.
I/B
Aufgaben
1. Informieren Sie sich im Internet, was eine Klothoide ist.
Welche Vorteile hat diese Kurve für die Konstruktion von Bahnführungssystemen?
Schreiben Sie die wesentlichen Aspekte in Ihr Heft.
Beschreiben Sie auch kurz die grundlegenden Merkmale einer Scheitelklothoide.
2. Beschreiben Sie die Energieumwandlungen (Lageenergie  Bewegungsenergie), die bei
einer Fahrt vom Anfangspunkt bis zum Endpunkt der Loopingbahn (Abb. 1) stattinden.
Vernachlässigen Sie die Reibung.
T
H
C
A
I
S
N
B
C
A
R
O
Abb. 1: Loopingbahn mit Startrampe
D
3. Die Starthöhe betrage 40 m. Der Looping habe eine maximale Höhe von 20 m.
Berechnen Sie die Geschwindigkeiten
V
– im Abschnitt D und
– im höchsten Punkt der Loopingbahn.
Der Energieerhaltungssatz hilft weiter. Vernachlässigen Sie die Reibung.
4. Die Kraft, mit der eine Person während der Fahrt durch die Achterbahn in ihren Sitz gedrückt
wird, steht senkrecht zur Bahn. Man bezeichnet sie als Normalkraft FN . Für ihre Berechnung
muss man die Erdanziehungskraft und die Zentrifugalkraft (Zentripetalkraft) berücksichtigen.
a) Beschreiben Sie, welche der genannten Kräfte in welchen Abschnitten der Bahn (siehe
Abb. 1) auf eine Person wirken, wenn diese die Bahn vollständig durchfährt.
Begründen Sie Ihre Antwort kurz.
b) Wenn man die Normalkraft durch die beschleunigte Masse dividiert, erhält man die Normalbeschleunigung
FN
.
m
Diese Größe wird bei Loopingbahnen oft in Vielfachen der Erdbeschleunigung g angegeben.
Man sagt z. B. „In diesem Punkt beträgt die Normalbeschleunigung 4 g“ und meint damit,
dass man sich dort viermal so schwer fühlt.
aN =
Gehen Sie für diesen Aufgabenteil davon aus, dass der Looping kreisförmig ist (r = 10 m).
27 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
8 von 16
Der Wagen startet aus einer Höhe von 40 m.
Berechnen Sie die Normalbeschleunigungen in den Abschnitten
– A,
– D,
I/B
m
)
s
m
– im höchsten Punkt des Kreisloopings (v = 19,81
)
s
– im tiefsten Punkt des Kreisloopings (v = 28
Geben Sie Ihre Ergebnisse in Vielfachen von g an. Beurteilen Sie, ob die Belastungen für
den menschlichen Körper gefährlich sind.
In Achterbahnen dürfen kurzzeitig bis zu 5 g wirksam werden.
5. Starten Sie die Computersimulation Looping.exe und machen Sie sich mit deren Funktionen
vertraut.
6. a) Wählen Sie einen Kreislooping und überprüfen Sie Ihre Ergebnisse aus Aufgabe 3
und 4 b) anhand der Kurven für Bahngeschwindigkeit und Normalbeschleunigung.
T
H
C
Gehen Sie mit dem Cursor auf das Diagramm, dann können Sie die entsprechenden Werte
ablesen.
I
S
N
Übertragen Sie die Kurven in Ihr Heft (Skizze oder Ausdruck).
b) Beschreiben Sie den Verlauf der Geschwindigkeitskurve und den Verlauf der Beschleunigungskurve mit Worten.
A
R
O
Erinnern Sie sich, dass die zweite Kurve (Normalbeschleunigung) angibt, wie stark die
Person im Wagen in den Sitz gedrückt wird.
V
7. Schalten Sie in der Computersimulation die Reibung (Luft- und Rollreibung) ein.
a) Starten Sie die Simulation mit einer Starthöhe von 40 m. Notieren Sie sich den Wert der
Geschwindigkeit, die der Wagen am Ende der Fahrt aufweist.
b) Berechnen Sie die kinetische Energie, die der Wagen nach Durchfahren der gesamten Bahn
hat (bewegte Masse: 200 kg). Vergleichen Sie diesen Wert mit der Energie im Startpunkt
(Lageenergie).
c) Geben Sie den Energieverlust aufgrund der Reibung in Prozent an.
8. a) Wählen Sie nun die klothoidenförmigen Loopingbahnen aus. Simulieren Sie Fahrten mit
einer Starthöhe von 40 m mit und ohne Reibung. Übertragen Sie einige Kurven in Ihr Heft
(Skizze oder Ausdruck).
b) Beschreiben Sie, wie sich die Beschleunigungskurven der Klothoide bzw. der aus Klothoide
und Kreis zusammengesetzten Bahn von denen des Kreisloopings unterscheiden.
Erklären Sie die Unterschiede. Begründen Sie, warum auf Jahrmärkten niemals kreisförmige
Loopings eingesetzt werden. Lesen Sie dazu auch den Text zur Flip-Flap-Achterbahn (M 4),
die 1895 gebaut, aber nach kurzer Zeit wieder geschlossen werden musste.
c) Die dritte Loopingbahn (Klothoide-Klothoide) hat einen kleinen (konstruktionsbedingten)
Nachteil, der sich vor allem bei großen Geschwindigkeiten bemerkbar macht und sich in
der Beschleunigungskurve verrät.
Nennen Sie das Problem und überlegen Sie, wie ein Fahrgast dies bemerken würde.
26 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
M4
9 von 16
Rückenschmerzen und Schleudertrauma garantiert –
der Flip-Flap-Looping von 1895
Zwei Artikel
[...] But the idea was revived at Coney Island’s
Sea Lion Park in 1895. Designed by Lina
Beecher, the Flip-Flap was another modest
single-looper, yet a bit grander in scale than
Europe’s early models. This time, a two
passenger car was hauled up a lift hill, made
a left-hand turn, and dived to whistle through
a 25-foot-tall loop.
Sadly, the Flip-Flap’s perfectly circular inversion was a literal pain in the neck; as riders
entered the base of the loop, they received
a sudden jolt, resulting in numerous
complaints of whiplash. The addition of
taller back supports in the seats did nothing
to alleviate the problem and the Flip-Flap
was razed within years of its debut.
I/B
(Quelle: http://www.thrillride.com/sonofbeast/sob.html)
nearly perfect circle, and the tight curve
coming in and out of the loop exerted high
G-forces-enough to break riders’ necks. The
Flip Flap was soon shut down.
T
H
C
(Quelle: http://www.oppapers.com/essays/Roller-Coasters/660123)
I
S
N
A
R
O
V
Foto: http://newsplusnotes.blogspot.com/2011/06/
blast-from-past-turning-you-upside-down.html
[...] The next signiicant attempt at a looping
roller coaster did not come along until 1895.
This is when Lina Beecher designed the Flip
Flap. However, the Flip Flap had a very terrible
law, its 25-foot vertical loop amounted to a
Foto: http://www.mainstgazette.com/2010
/04/fantastically-successful-coney-island.
html
Abb. 1: Historische Aufnahme des Flip-Flap Loopings
Abb. 2: Modell der Flip-Flap-Achterbahn
27 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
10 von 16
M5
Wann fällt man raus? – Die Mindestgeschwindigkeit angeben
Die Kräfte im höchsten Punkt der Bahn untersuchen
Foto: dpa/picture-alliance
I/B
Eine Loopingbahn im Spreepark Berlin
T
H
C
Aufgaben
1. Damit der Wagen den höchsten Punkt gerade noch durchfahren kann, ohne die Bahn zu
verlassen, muss er dort eine bestimmte Mindestgeschwindigkeit vmin aufweisen. Diese
erzeugt nämlich eine Zentrifugalkraft, welche die Erdanziehungskraft in diesem Punkt
kompensiert (oder anders formuliert: Die Erdanziehungskraft stellt in diesem Punkt die für
die Kreisbahn notwendige Zentripetalkraft dar).
I
S
N
Leiten Sie mithilfe dieses Ansatzes her:
A
R
O
Für die Mindestgeschwindigkeit, die ein Wagen im höchsten Punkt haben muss, gilt:
vmin =
rL ⋅ g , wobei rL der Radius des Kreisloopings ist.
2. Damit der Wagen die Mindestgeschwindigkeit im höchsten Punkt erreicht, muss er aus einer
bestimmten Höhe auf der Rampe gestartet werden.
V
Leiten Sie mithilfe des Energieerhaltungssatzes und der Formel aus Aufgabe 1 her:
Für die Mindeststarthöhe gilt ohne Reibung: hmin = 2,5 • rL .
3. Berechnen Sie vmin und hmin für den Kreislooping. Überprüfen Sie Ihre Berechnungen mithilfe
der Computersimulation.
4. a) Bestimmen Sie durch Probieren mithilfe der Computersimulation die Mindeststarthöhe
hmin (keine Reibung) und die Mindestgeschwindigkeit vmin im höchsten Punkt bei den Klothoidenloopings.
b) Überlegen Sie, warum die Mindestgeschwindigkeit vmin bei den Klothoidenloopings geringer
ist als beim Kreislooping, obwohl alle die gleiche Höhe haben.
5. Wählen Sie nun eine Starthöhe, die kleiner ist als die Mindeststarthöhe hmin – beispielsweise
20 m. Der Wagen wird an einem bestimmten Punkt der Bahn abstürzen, also die Loopingbahn verlassen, falls er nicht durch spezielle Bügel gesichert ist.
a) Man könnte denken, der Körper stürzt ab, weil er in dem kritischen Punkt keine Geschwindigkeit mehr hat (also v = 0 m/s). Dies ist aber nicht der Fall, wie die Simulation verdeutlicht.
Erklären Sie die physikalischen Zusammenhänge.
b) Bezeichnen Sie die Bahn, die der Körper beim Absturz aus der Loopingbahn beschreibt.
Um welche Bahnform handelt es sich? Fertigen Sie dazu eine Skizze an.
26 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
M6

11 von 16
Tippkarten
M3
Tipp 1
Aufgabe 3
Ansatz: Die Lageenergie im Startpunkt wird vollständig in Bewegungsenergie (kinetische Energie) umgewandelt.
Tipp 2
Ekin = ELage
Tipp 3
1
2
I/B
m ⋅ v 2 = m ⋅ g ⋅ hStart
Tipp 4

Im höchsten Punkt des Looping hat der Körper gegenüber dem Startpunkt
den Betrag hStart – hhöchster Punkt an Höhe verloren.
ìï Tipp 1
ï Die gesuchte Beschleunigung ergibt sich aus der Kräftezerlegung (BeschleuAufgabe 4b ï
ïï nigungszerlegung) an der schiefen Ebene.
(Abschnitt A) í
ïî Tipp 2 a = g ⋅ cos(α)
î
M3
ï Tipp 1
í
ïï Der Fahrgast spürt seine Gewichtskraft und dazu die Zentrifugalkraft
ïï aufgrund der Bewegung auf der Kreisbahn.
ïì
v
N
(tiefster
Punkt)
T
H
C
I
S
N
2
Tipp 2
(höchster
Punkt)

M5
Aufgabe 1
M5
Aufgabe 2

rKreis
îï
í Tipp 1
ïï Der Fahrgast spürt die Zentrifugalkraft, die aber um seine Gewichtskraft
ïï vermindert ist, denn beide Kräfte wirken in entgegengesetzte Richtungen.
ïì
v
A
R
O
V

a Bahn = 1⋅ g +
Tipp 2
a Bahn =
Tipp
FZ = FG
2
Hoch
rKreis
− 1⋅ g
Tipp 1
Die Energie im Startpunkt (Lageenergie) entspricht der Summe aus Lageenergie und kinetischer Energie im höchsten Punkt des Loopings.
Tipp 2
2
m ⋅ g ⋅ hStartmin = m ⋅ g ⋅ (2 ⋅ rL ) + 21 ⋅ m ⋅ vmin
Tipp 3
vmin =
rL ⋅ g
Ersetzen Sie die Mindestgeschwindigkeit vmin durch den Ausdruck
und fassen Sie zusammen.
M5
Aufgabe 4
Tipp 1
Beachten Sie, dass die Radien im höchsten Punkt der verschiedenen Loopingarten nicht gleich sind.
Tipp 2
Argumentieren Sie mit der Formel: FZ =

rL ⋅ g
m ⋅ v2
r
27 RAAbits Physik Mai 2012
18. Die Physik einer Loopingbahn untersuchen
12 von 16
Erläuterungen und Lösungen
Unterrichtseinstieg
Stellen Sie zu Beginn der Unterrichtseinheit einige Fragen:
I/B
– Welche Geschwindigkeiten und welche Beschleunigungen nimmt ein Mensch wahr, wenn
er eine Loopingbahn durchfährt?
– Warum sind Loopings in Achterbahnen niemals kreisförmig gebaut?
– Wann fällt man aus der Loopingbahn heraus?
Mithilfe einer Computersimulation beantworten die Schüler Fragen dieser Art und erhalten
einen Einblick in die spannende Physik von Loopingbahnen.
M 3
Ideen zur Loopingbahn – Bewegungsgrößen berechnen
Lösungen
1. Eine Klothoide ist eine Kurve, bei der die Krümmung der Kurve
proportional zur Länge der Bahn ist. Das bedeutet: Je weiter man
auf der Klothoidenbahn fährt, desto enger wird die Kurve.
Klothoiden werden gerne für den Anfang oder das Ende von Kurven
im Straßen- oder Schienenbau verwendet, weil sie eine sanfte
Zunahme der Krümmung gewährleisten. So steigt die Zentripetalbeschleunigung nur langsam an.
T
H
C
I
S
N
Eine Scheitelklothoide hat folgende Merkmale:
– Sie besteht aus zwei Klothoidenästen.
A
R
O
– Die Äste sind im Scheitelpunkt so aneinandergefügt, dass ein glatter Übergang von einem
Kurvenstück zum anderen gewährleistet ist.
2. Am Startpunkt hat der Körper nur Lageenergie. In den Abschnitten A, B und C der Bahn
wird diese Lageenergie zunehmend in kinetische Energie umgewandelt. Im Abschnitt D ist
die Lageenergie vollständig in kinetische Energie umgesetzt. Wir legen unser Koordinatensystem nämlich so, dass auf der Höhe von D die Lageenergie gleich null ist.
V
Sobald der Wagen den Looping befährt, verwandelt sich die kinetische Energie wieder in
Lageenergie. Im höchsten Punkt hat der Körper kinetische Energie und Lageenergie, die
beim Verlassen des Loopings vollständig in Bewegungsenergie umgewandelt wird.
3. Die Lageenergie im Startpunkt wird vollständig in kinetische Energie umgewandelt.
Daher gilt:
Ekin = ELage
1
2
mv 2 = mghStart
⇔
v=
2g ⋅ hStart =
2 ⋅ 9,81⋅ 40
m
m
km
= 28
≈ 101
s
s
h
Dies sind etwa 101 km/h.
Wenn der Körper sich im höchsten Punkt des Loopings beindet, hat er gegenüber dem
Startpunkt auf der Rampe 20 m an Höhe verloren. Dieser Verlust an Lageenergie wurde
vollständig in kinetische Energie umgewandelt. Daher gilt:
v=
2g ⋅ hHP =
26 RAAbits Physik Mai 2012
2 ⋅ 9,81⋅ 20
m
m
km
= 19,81 ≈ 71
s
s
h