Ubungsaufgaben für die Physik II - Institut für Physik

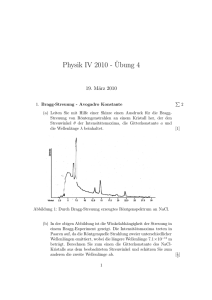
Universität Rostock
Institut für Physik
Prof. Dr. H.-J. Fitting
1989 - 1997
Übungsaufgaben für die Physik II
Aufgabe 1:“Fourieranalyse”
Drücken Sie eine periodische Dreieckfunktion
y=x
−
π
π
≤x≤+
2
2
3
π
≤x≤ π
2
2
durch ihre harmonischen Grundschwingungen aus.
y =π−x
Aufgabe 2:“Lichtdispersion”
Bestimmen Sie aus der Dispersionskurve des Lichtes in Quarzglas mit den
Brechungsindices
n(λblau = 486nm) = 1, 4631
n(λrot = 656nm) = 1, 4563
die Gruppengeschwindigkeit vg des Lichtes um den Mittelwert λ̄ ' 570 nm und setzen Sie
den Wert in Bezug zur Phasengeschwindigkeit!
Aufgabe 3: “Messung der Lichtgeschwindigkeit”
Ergibt sich bei der Foucault’schen Drehspiegelmessung der Lichtgeschwindigkeit als Abweichung ∆s ein Strich oder ein Punkt, warum?
Aufgabe 4: “Akustischer Doppler-Effekt”
Ein ruhender Beobachter hat den Eindruck, dass sich die Schallfrequenz eines vorbeifahrenden Motorrades ändert. Können Sie den Frequenzverlauf als Funktion der Zeit berechnen
und darstellen? Wie gross ist die Frequenzdifferenz zwischen den Positionen “weit links” und
“weit rechts” vom Beobachter?
(Geschwindigkeit des Motorrades v = 100 km/h,
Abstand des Beobachters zur Straße d = 10 m,
Frequenz des ruhenden Motorrades f0 = 500Hz,
Schallgeschwindigkeit c = 331 m/s).
1
Aufgabe 5: “Überschallflugzeug”
Sie hören ein über Sie hinweg fliegendes Flugzeug erst nach einem Knall, bei dem es sich bereits in einem Winkel von 30o (45o oder 60o ) zum Zenit befindet. Welche Geschwindigkeit(en)
besitzt das Flugzeug?
Aufgabe 6: “Michelson-Experiment”
Um wieviel Interferenzstreifen ändert sich das Bild des Michelson-Interferometers im Originalaufbau mit Spiegelabständen l = 32 m (siehe Vorlesung), wenn es um 90o zur Erdbewegung
(Evolution) gedreht wird und ein Äther für die Lichtausbreitung angenommen wird? (Monochromatisches Licht λ = 640 nm) Was zeigt sich jedoch und welcher Schluß muß gezogen
werden?
Aufgabe 7: “Relativistischer Elektronenstrahl”
Ein 100 MeV-Elektron mit β = 0, 999987 fliegt durch eine 3 m lange Röhre. Welche Röhrenlänge
“sieht” das Elektron und welche Flugzeit wird von ihm registriert?
Aufgabe 8: “Myon-Lebensdauer”
Die mittlere Lebensdauer eines Myons nach Abbremsung in einem Bleiblock beträgt 2, 2µs.
Die mittlere Lebensdauer eines Myons in der kosmischen Strahlung von der Erde aus gemessen beträgt dagegen 16µs. Wie hoch ist die Geschwindigkeit des kosmischen Myons?
Aufgabe 9: “Masseloses Teilches mit v=c”
Ein masseloses Teilchen bewege sich mit einer Geschwindigkeit v=c vom Beobachter fort.
Dann verfolgt der Beobachter das Teilchen mit einer Geschwindigkeit von v=0,9c. Welche
Teilchengeschwindigkeit mißt der Beobachter nun?
Aufgabe 10: “Zwei Elektronenkanonen”
Zwei Elektronenkanonen, fest im System So , schießen in entgegengesetzte Richtung Elektronen mit v = 2, 5 × 108 m/s ab. Die Differenz beider Geschwindigkeiten würde Überlichtgeschwindigkeit bedeuten. Wie groß ist jedoch die Relativgeschwindigkeit des einen Strahls
S1 zum anderen S2 ?
Aufgabe 11: “Massenverdopplung”
Wie groß ist die Geschwindigkeit eines Teilchens, wenn seine Masse gleich dem Doppelten
der Ruhemasse ist?
2
Aufgabe 12: “Freier Fall - relativistisch”
Berechnen Sie die Endgeschwindigkeit nach Durchfallen der Höhe h im homogenen Gravitationsfeld g in relativistischer Form.
Aufgabe 13: “Gewicht der Brennmaterialien und Verbrennungsstoffe”
Beantworten Sie die alte Scherzfrage:
Was wiegt mehr, der Holzstoß oder Asche und Rauch ?
Aufgabe 14: “Massenverlust der Sonne”
Der Energiefluß von der Sonne beträgt auf der Erdoberfläche etwa 1 kW/m2 .
Wie groß ist der Massenverlust der Sonne pro Jahr?
Aufgabe 15: “Energiezunahme”
Welche Energien müssen einem Elektron zugeführt werden, um gleiche Geschwindigkeitserhöhungen v= 0,01 c zu bewirken, wenn seine Geschwindigkeit
a) v = 0,10 c
b) v = 0,98 c
beträgt?
Aufgabe 16: “Beschleuniger”
Ein Physiker gefragt, wie schnell die Elektronen in seinem 2 MeV-Beschleuniger fliegen, tippt
in seinen Taschenrechner
1
IN V COS SIN
x
und erhält 0,979. Er sagt , sie fliegen mit 97.9 % der Lichtgeschwindigkeit.
Können Sie das erklären?
2000 : 512 + 1 =
Aufgabe 17: “Radarkontrolle”
Wie groß ist die Schwebungsfrequenz bei der Überlagerung von ausgesendetem und reflektiertem Radarstrahl (λ = 6 cm), wenn das zu messende Fahrzeug sich mit der Geschwindigkeit
v = (10 - 200) km/h longitudinal fortbewegt?
Aufgabe 18: “Doppler-Rotverschiebung”
Entfernte Galaxien besitzen einen Rotverschiebungsparameter Z = ∆λ/λ0 < 0, 5.
Wie groß ist die Fluchtgeschwindigkeit?
Welche Modelle ergeben sich für das Weltall?
3
Aufgabe 19: “Lichtgeschwindigkeit im Wasserstrahl”
Mit welcher Wellenlängendifferenz passiert ein Lichtstrahl (λ = 500 nm) ein 10 m langes
Wasserrohr, in dem Wasser mit 10 m/s in Lichtrichtung strömt, gegenüber dem Rohr mit
ruhender Wassersäule?
Aufgabe 20: “Photonenmasse”
Wie groß ist die relativistische Masse eines Photons der Wellenlänge λ = 600 nm?
Aufgabe 21: “Paarbildung”
Wie hoch muß die Energie eines γ-Quants mindestens sein, damit es in ein Elektron und ein
Positron zerfallen kann?
Aufgabe 22: “Elektron-Positron-Stoß”
In modernen Teilchenbeschleunigeranlagen läßt man hochenergetische Elektronen (e− ) und
Positronen (e+ ) frontal aufeinanderstoßen. Leiten Sie aus der Kenntnis der Strahlenenergie
im Schwerpunktsystem von e− und e+ einen Ausdruck für diejenige Energie ab, die man im
Ruhesystem von z.B. e− messen würde. Setzen Sie dazu an, daß sich e− und e+ relativ zu ihrem gemeinsamen Schwerpunkt mit den Geschwindigkeiten v bzw. -v aufeinanderzubewegen.
Welche Schlußfolgerung können Sie aus Ihrem Ergebnis für den Bau von Beschleunigeranlagen ziehen? Denken Sie dabei daran, daß die erforderlichen Energien sehr hoch sind, etwa
im Bereich von einigen GeV .
Aufgabe 23: “Relativistische Transformation elektro-magnetischer Felder”
Erklären Sie aus den Transformationsgleichungen für elektromagnetische Felder die Existenz
des Durchflutungsgesetzes und die Induktionsgleichung.
Aufgabe 24: “Synchrotron”
Am Fermi National Accelerator Laboratory in Batavia (Illinois, USA) werden Protonen auf
eine kinetische Energie von 500 MeV beschleunigt. Der Beschleuniger ist als Synchrotron
aufgebaut und hat den Krümmungsradius R = 750 m. Berechnen Sie
- den LORENTZ-Faktor γ
- das erforderliche magnetische Feld (in Tesla).
Aufgabe 25: “Gravitative Rotverschiebung”
Berechnen Sie die gravitative Rotverschiebung der grünen H-Linie λ0 = 486 nm im Spektrum
des Sirius Begleiters M = 0, 85MSonne und R = 0, 0272RSonne . Wie groß müßte andererseits
seine Fluchtgeschwindigkeit für die Doppler-Rotverschiebung sein?
Diskutieren Sie die Ergebnisse.
4
Aufgabe 26: “Gravitative Lichtablenkung”
Bei einer Sonnenfinsternis beobachtet man Fixsterne am verdunkelten Sonnenrand vorbei
unter einer Winkelabweichung δ. Berechnen Sie δ mit der in der Vorlesung gegebenen Formel. Vergleichen Sie die gravitative Ablenkung mit der gewöhnlichen Fixsternaberration!
Aufgabe 27: “Periheldrehung der Planetenbahn”
Nennen Sie die Ursache für die Periheldrehung der Planetenbahnen.
Aufgabe 28: “Gravitationsdruck”
Leiten Sie die Schwerebeschleunigung g(r < R) im Innern einer homogenen Massekugel M
des Radius R her. Welcher Gravitationsdruck ergibt sich in der Kugelmitte?
Hinweise:
Zeigen Sie zunächst, daß derjenige Massenanteil, der sich in der Kugelschale außerhalb von
r befindet, keine resultierende Kraft auf die Probemasse ausübt. Dies bedeutet also, daß für
r < R gilt: F = GM m/r 2 . Um dieses Ergebnis zu erhalten, können Sie den folgenden Weg
einschlagen:
(1) Denken Sie sich eine Hohlkugel und Ihre Probemasse im Innern dieser Kugel. Die Kugelschale habe die Dicke ∆R.
(2) Bestimmen Sie die resultierende Kraft, die diese Massenschale auf die Probemasse ausübt.
Sie muß gleich Null sein, und zwar für alle Positionen der Probemasse im Innern der Kugel.
(Hieraus folgt dann, daß F = GM m/r 2 sein muß.)
(3) Um die resultierende Kraft zu erhalten, müssen Sie die Kraftbeiträge aller Massenelemente aufsummieren. Dies führt also auf eine Volumenintegration.
(4) Zerlegen Sie hierzu die Kugelschale in Kreisringe, die zum Beispiel senkrecht auf der
x-Achse stehen.
(5) Rechnen Sie die resultierende Kraft zunächst von einem Ring auf die Masse aus.
(6) Summieren (d.h. integrieren) Sie über alle diese Kreisringe.
Aufgabe 29: “Kernfusion in Sternen”
Schätzen Sie die Energiefreisetzung Eex bei der Nettoreaktion der Proton-Proton-Kernfusion
in Sternen
4p → α + 2β + + 2γ + 2ν + Eex
ab.
Aufgabe 30: “Schwarze Löcher”
Welche Bedingung gilt für die Masseverteilung eines Sterns, damit er zum “Schwarzen Loch”
wird?
5
Aufgabe 31: “Stefan–Boltzmann–Gesetz”
Leiten Sie aus der Planck’schen Strahlungsformel durch Integration über alle Wellenlängen
das Stefan–Boltzmann–Gesetz für die Gesamtstrahlungsleistung her!
Aufgabe 32: “Wien’sches Verschiebungsgestz”
Zeigen Sie, daß sich das Wien’sche Verschiebungsgesetz für die Wellenlänge der maximalen
Strahlungsleistung direkt aus dem Planck’schen Strahlungsgesetz herleitet!
Aufgabe 33: “Strahlung einer Ofenplatte”
Wie groß sind Strahlungsleistung und wahrscheinlichste Wellenlänge einer 1m2 großen, schwarzen Ofenplatte, die einmal auf 100 o C, dann auf 1000 o C erhitzt wird?
Aufgabe 34: “Photoeffekt”
Ein monochromatischer Lichtstrahl der Wellenlänge λ = 400 nm und der Intensität I0 =
W
3 · 10−9 m
2 fällt senkrecht auf eine Photokatode mit der Austrittsarbeit Ψ A = 2.0 eV. Bestimmen Sie bei vollständiger Absorption desselben:
(a) die pro m2 und Sekunde absorbierte Energie in der Photokatode
(b) die maximal mögliche Anzahl der pro m2 und Sekunde emittierten Photoelektronen
bei einer Quantenausbeute η = 1
(c) die maximale kinetische Energie der Photoelektronen!
Aufgabe 35: “Welle-Quasiteilchen”
Sowohl die Amplitude als auch die Frequenz einer ebenen elektromagnetischen Welle werden
um den Faktor 2 vergrößert. Um welchen Faktor ändert sich die Anzahl der Photonen pro
m2 und Sekunde?
Aufgabe 36: “Compton-Effekt”
Ein Photon der Energie 10 keV stößt mit einem freien, ruhenden Elektron und wird um den
Winkel 60o gestreut.
Bestimmen Sie
(a) die Änderung von Energie, Frequenz und Wellenlänge des Photons
(b) die kinetische Energie, den Impuls und die Richtung des gestoßenen Elektrons!
Aufgabe 37: “Interpretation des Compton-Effekts”
Warum überzeugt Sie der Compton-Effekt davon, daß elektromagnetische Strahlung als
Teilchenstrom aufgefaßt werden kann? Wie würden Sie den Begriff “Photon” einem noch
“unwissenden” Fachkollegen erklären?
6
Aufgabe 38: “Thermische Neutronen”
Thermische Neutronen befinden sich mit anderen Teilchen bei Raumtemperatur (TR '
300 K, kB TR ' 0.025 eV) im thermischen Gleichgewicht. Wie groß ist die mittlere kinetische Energie eines thermischen Neutrons, wie groß die zugehörende Wellenlänge?
Aufgabe 39: “Elektronenbeugung am Doppelspalt”
Zwei sehr schmale Spalte haben einen Abstand von 10 µm. Ein Elektronenstrahl mit der
Energie 10 eV treffe auf die Spalte. Ein Beobachtungsschirm befinde sich 1m hinter den
Spalten. Wie groß ist der Abstand zwischen zwei aufeinanderfolgenden Minima auf dem
Schirm?
Aufgabe 40: “Elektronenbeugung am Kristall”
Ein tetragonaler Kristall mit den Atomabständen a = 2.0 Å in X-Richtung und b = 1.5 Å
in y-Richtung wird senkrecht (z-Richtung) mit Elektronen der Energie 90 eV beschossen.
Berechnen und zeichnen Sie das Beugungsbild in Reflexion auf einen 10 cm entfernten Fluoreszenzschirm. In welche Richtung verschieben sich die Reflexe, wenn die Elektronenenergie
erhöht wird?
Aufgabe 41: “Unschärfe eines Elektrons”
Der Ort eines Elektrons ist mit der Unschärfe von 0.1 Å bestimmt worden. Berechnen Sie die
Unbestimmtheit seines Impulses und seiner Energie, wenn die Energie in der Größenordnung
von 1 keV liegt.
Aufgabe 42: “Elektron im Potentialkasten”
Ein Elektron befindet sich im 3-dimensionalen Potentialkasten der Abmessung 2Å×2Å×2Å.
Das Potential an diesen Wänden hat den Wert ∞. Ermitteln Sie die möglichen Wellenvektoren für die ersten 4 Energiewerte des Elektrons. Geben Sie diese Energiewerte und ihren
Entartungsgrad an!
Aufgabe 43: “Tunneleffekt”
Berechnen Sie die Tunnelwahrscheinlichkeit eines Elektrons mit der kinetischen Energie 10
eV durch einen Potentialwall der “Höhe” U0 = 15 eV und der Breite l = 2 Å!
Aufgabe 44: “Harmonischer Oszillator”
Wie ist das Schwingungsverhalten eines Harmonischen Oszillators in der Quantenmechanik
charakterisiert? Wo finden Sie Anwendungen in der Natur?
7
Aufgabe 45: “Spektrum des Wasserstoffatoms”
Bestimmen Sie die jeweils größten und kleinsten Energiewerte hf und den zugehörigen Wellenlängenbereich der Lyman-Serie, der Balmer-Serie und der Paschen-Serie des Wasserstoffatom-Spektrums!
Aufgabe 46: “Magnetische Momente der Elektronenbahnen”
Bestimmen Sie den elektrischen Strom des Elektrons in den ersten 3 Bohrschen Bahnen
(n=1;2;3)! Berechnen Sie auch die magnetischen Dipolmomente für jeden der Fälle.
Aufgabe 47: “Quantendefekte bei Alkali Atomen”
Berechnen Sie die Wellenlänge der gelben Natriumlinie mit den Serienformeln und Quantendefekten aus der Vorlesung.
Aufgabe 48: “Stern-Gerlach-Versuch”
Ein Ag 0 -Strahl fliegt mit v = 700 ms−10 entlang der x-Achse durch ein inhomogenes Magnetfeld mit konstantem Gradienten dB/dz = 300T m−1 in z-Richtung. Die Länge des Magnetfeldes beträgt 0.1 m. Man berechne die maximale Winkeldifferenz zwischen dem “Spin-up”
und dem “Spin-down” Strahl.
Aufgabe 49: “Spin-Bahn-Aufspaltung”
Berechnen Sie die beiden Wellenlängen der gelben Na-Doppellinie.
Aufgabe 50: “Einstein-deHaas-Effekt”
Geben Sie eine möglichst realistische Meßprozedur zur Bestimmung des gyromagnetischen
Verhältnisses im Einstein-deHaas-Experiment an.
Aufgabe 51: “Spin-Bahn-Kopplung”
Finden Sie Analogien zwischen den Drehimpulsen ~j, ~l und ~s des Elektrons im Atom und
entsprechenden Drehimpulsen im Kreisel
a) kräftefrei
b) nicht kräftefrei.
Aufgabe 52: “Elektronenspinresonanz - ESR”
Welche Frequenz ist nötig, um in einem Magnetfeld von 0,1 T Elektronen-Spin-übergänge
von der parallelen zur antiparallelen Ausrichtung und umgekehrt zu induzieren?
8
Aufgabe 53: “Zeeman-Effekt”
Zeichnen Sie die Zeeman-Aufspaltung in den Linien der Balmer-Serie des Wasserstoffatoms.
Aufgabe 54: “Linienverbreiterung im Emissionsspektrum”
Vergleichen Sie die natürliche Linienverbreiterung der Balmer-Serie Hα , Hβ im Wasserstoffatom bei der Annahme der mittleren Lebensdauer angeregter Zustände τ ≈ 10−8 s mit der
Dopplerverbreiterung bei Raumtemperatur.
Aufgabe 55: “Russel-Saunders-Kopplung”
~ und Spin S
~ fr die Terme 2 P1/2 , 2 P3/2 ,
Zeichnen Sie die Vektorgerüste von Drehimpuls L
4
D1/2 , D3/2 .
4
Aufgabe 56: “Orthohelium”
Warum gibt es beim Orthohelium keinen 2P −→ 1S Übergang?
Aufgabe 57: “Landè-Faktor”
Bestimmen Sie den Landè-Faktor für die Terme
2
P1/2 , 2 P3/2 , 4 D1/2 , 4 D3/2 .
Aufgabe 58: “Charakteristische Röntgenstrahlung”
Berechnen Sie die Energie und Wellenlänge der Kα - Linie für Cu nach dem Moseley-Gesetz
und vergleichen Sie den Wert mit Tabellendaten.
Aufgabe 59: “Bragg-Gesetz”
Ein kubischer MgO-Kristall mit der Gitterkonstanten a = 4, 2Å dient als Monochromator
Al
für die AlKα - Strahlung, hfKα
= 1487 eV. Unter welchem Winkel entsteht der Bragg-Reflex?
Erklären Sie den Vorgang.
Aufgabe 60: “Periodensystem der Elemente”
Wie ordnen sich die Lantaniden mit welcher Elektronenkonfiguration ins Periodensystem der
Elemente ein ?
Aufgabe 61: “Hund‘sche Regel - Bindungsvalenzen”
Warum gehen Bor einwertige, Kohlenstoff vierwertige und Stickstoff dreiwertige Bindungen
ein ?
9
Aufgabe 62: “Molekularorbitale”
Zeichnen Sie ein Tetrachlorkohlenwasserstoffmolekül mit seinen Bindungsorbitalen. Erläutern
Sie die Bindungsart und berechnen Sie die Winkel zwischen den Bindungen.
Aufgabe 63: “Molekülschwingungen”
Welche Molekülspektren kennen Sie und wie entstehen Sie ?
Aufgabe 64: “Lumineszenz”
Charakterisieren Sie den Unterschied zwischen Fluoreszenz und Phosphoreszenz.
Aufgabe 65: “Rutherfordstreuung”
Wie verhalten sich die Streuwahrscheinlichkeiten geladener Teilchen an (schweren) Atomkernen in 10o - Vorwärtsstreuung, 45o , 90o - Seitwärtsstreuung und 180o - Rückwärtsstreuung
(Backscattering)?
Konstruieren Sie hieraus ein grobes Polardiagramm.
Wie ergibt sich der totale Wirkungsquerschnitt δtot und die mittlere freie Weglänge λ?
Aufgabe 66: “Kernfusion”
Bestätigen Sie die Energiebilanz für die Reaktion
7
4
3 Li + p −→ 2 2 He + 17, 2 M eV .
Aufgabe 67: “Kernspaltung”
Wie lautet die Reaktion für die Spaltung von
reaktion?
235
U und wie macht man hieraus eine Ketten-
Aufgabe 68: “Künstliche Kernumwandlung”
Geben Sie ein Beispiel für eine künstliche Kernumwandlung an und erläutern Sie den Prozeß.
Aufgabe 69: “Radioaktive Altersbestimmung”
Auf welchen Teil ist die 14 C-Radioaktivität eines organischen Fossils abgesunken, wenn es
etwa 20 000 Jahre alt ist? Die Halbwertzeit des 14 C-Isotops beträgt 5680 a.
10