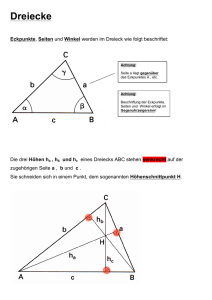
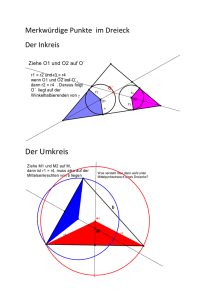
Höhenschnittpunkt eines Dreiecks

2-dimensionale Vektorrechnung
Dreiecke
Höhenschnittpunkt:
Gegeben sind die Punkte A, B und C
eines Dreiecks. Gesucht ist der
Höhenschnittpunkt des Dreiecks.
Lösungsweg:
Der
Höhenschnittpunkt
ist
der
Schnittpunkt der Höhenlinien. Eine
Höhenlinie geht durch einen Punkt des Dreiecks und ist normal auf die
gegenüberliegende Seite.
Bestimmung der Höhenlinie ha:
1. BC =C-B
2. Bestimmung des Normalvektors n BC (Normalvektor von BC )
3. ha: x =A+s. n BC
Bestimmung der Höhenlinie hb:
4. AC =C-A
5. Bestimmung des Normalvektors n AC (Normalvektor von AC )
6. hb: x =B+t. AC
Berechnung des Höhenschnittpunktes
7. Bestimmung des Schnittpunktes von ha und hb
Gerechnetes Beispiel:
Die Punkte A(-8|3), B(2|7) und C(2|-13) bilden ein Dreieck. Bestimme den Höhenschnittpunkt.
Lösung:
Der Höhenschnittpunkt ist der Schnittpunkt der Höhenlinien. Eine Höhenlinie geht
durch einen Punkt des Dreiecks und ist normal auf die gegenüberliegende Seite.
Bestimmung der Höhenlinie ha:
 2   2  0 
 -   = 

BC =C-B= 
 −13   7   − 20 
⇒ Richtungsvektor von ha ist normal auf BC . Man
erhält den Vektor (1|0)
 − 8  1 
 +s  
 3  0
ha: x = 
Bestimmung der Höhenlinie hb:
 2   − 8   10 
 -   = 

AC =C-A= 
 −13   3   −16 
⇒ Richtungsvektor von hb ist normal auf AC . Man
erhält den Vektor (8|5)
www.matheprofi.at
2-dimensionale Vektorrechnung
 2
7
Dreiecke
8
 5
hb: x =   +t  
Berechnung des Höhenschnittpunktes durch Bestimmung des Schnittpunktes von ha
und hb: Aus der Geraden ha erhält man: x=-8+s und y=3. Aus hb folgt: x=2+8t und
y=7+5t. Wenn man sowohl x als auch y gleichsetzt, so erhält man ein
Gleichungssystem mit den Unbekannten s und t:
-8
3
+s =
=
2 +8t
7 +5t ⇒ t=-4/5
Diesen Wert setzt man in die Gleichung der Geraden hb ein und erhält:
 2
8
 2
 − 32 / 5   − 22 / 5   − 4,4 
 =

3   3 
 = 
H=   +(-4/5).   =   + 
7
 5  7   − 4  
www.matheprofi.at