Der Umkreis

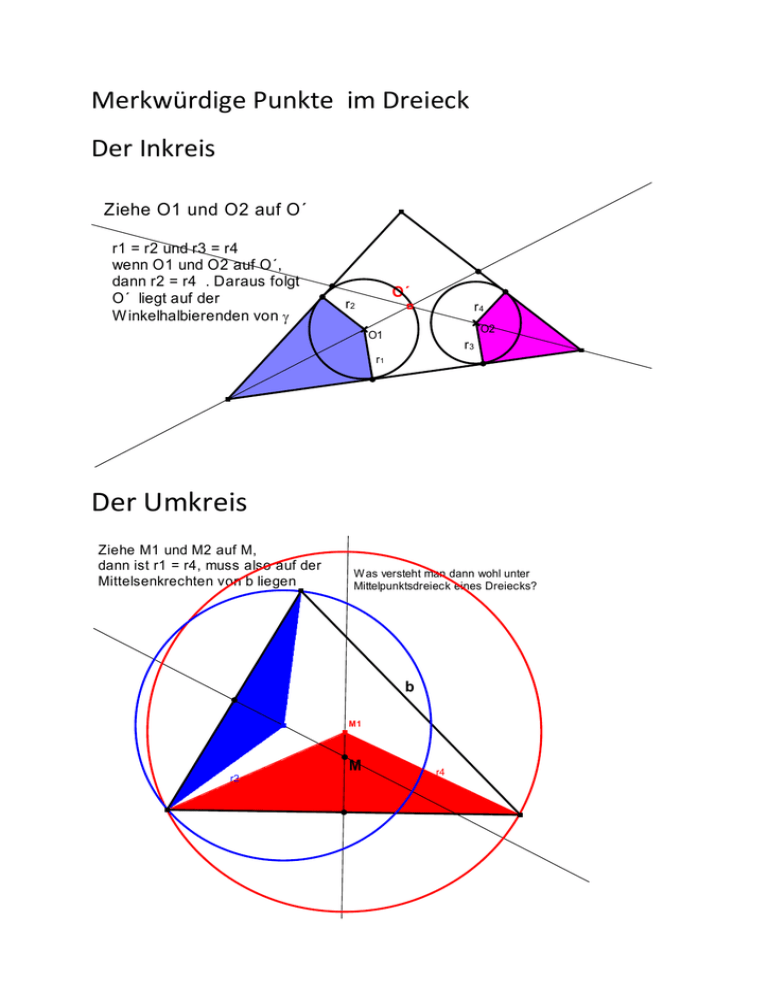
Merkwürdige Punkte im Dreieck Der Inkreis Ziehe O1 und O2 auff O´
r1 = r2 und r3 = r4
w nn O1 und O2 auf O´,
we
dann r2 = r4 . Daraus folgt
O´ liegt auf der
W inkelhalbierenden von γ
O´
r2
r4
O2
O1
r3
r1
Der Umkreis Ziehe M1 und M2 auff M,
dann ist r1 = r4, muss also auff der
Mittelsenkrechten von b liegen
W as versteht man dann wohl unter
Mittelpunktsdreieck eines Dreiecks?
r1
b
M2
M1
M
r2
r4
r3
Umfangswinkel über c 28,1 °
Der Umfangswi
w nkel über c ist halb so
groß wi
w e der Mittelpunktswi
w nkel über
dieser Seite
28,1 °
43,09 °
43,09 °
86,18 °
56,19 °
Schwerpunkt zwei mal 2. Strahlensatz
Die Scheitelabschnitte
1:2
also die Paralelabschnitte 1 : 2
Die Parallelabschnitte 1 : 2
also die Scheitelabschnitte 1 : 2
1
12,02 cm
2
7,63 cm
1´
S
10,05 cm
S´
2´
Das gleiche Vorgehen wäre mit der dritten
Schwerelinie möglich. Also muss S auch auf
der 3. Schwerelinie liegen
Der Höhenschnittpunkt Mit
itte ndr
d re ie
i ck, Um
U dr
d re ie
i ck,
Die Höhen im Mittendreieck sind Mittelsenkrecht
im Umdreieck.
Diese schneiden sich in einem Pukt. Also
schneiden sich die Höhen auch in einem Punkt.
H
Der Höhenschnittpunkt als dritter Punkt der Euler­Geraden 1,813 cm
3,626 cm
d(S;H)/d(M;S)
2
M
S
H
Konstruiere Dreieck, M und S. Zeichne die Gerade durch M und S. Verlängere MS über S hinaus um 2* MS . Den Punkt nennen wir vorgreifend H´. Verbinde C mit H´. Du erhältst eine Strahlensatzfigur. Begründe! Also ist die Gerade CH´ lotrecht auf c. Dieses Verfahren kansst du mit jeder Mittelsenkrechnte durchführen Also liegt H´auf jeder Höhe, ist also Höhenschnittpunkt. Nebenwinkel 70 °
70 °
20 °
20 °
Nebenwinkel ergänzen sich zu 180° Scheitelwinkel sind gleich groß, weil sie Nebenwinkel des gleichen Winkels sind Die Winkelhalbierenden eines Winkels und seines Nebenwinkels stehen lotrecht aufeinander. Ein Außenwinkel eines Dreiecks ist gleich der Summe der nicht anliegenden Innenwinkel. Das Höhenfußpunktdreieck Q
R
P
Zeichne das Höhenfußpunktdreieck PQR mit seinen Winkelhalbierenden und seinem Inkreis. Errichte in den Höhenfußpunkten die Senkrechten. Du erhältst ein Dreieck, in dem die Punkte PQR Höhenfußpunkte sind. Wie lässt sich dies beweisen? (s. Abbildung). Im Höhenfußpunktdreieck sind die Winkelhalbierenden Höhen des Ausgangsdreieck. Wenn wir bewiesen haben, dass sich die Winkelhalbierenden in einem Punkt schneiden, so haben wir hiermit auch bewiesen, dass sich die Höhen in einen Punkt schneiden. Zu einem Höhenfußpunktdreieck gibt es vier Dreiecke. Stumpfwinklige Dreiecke Durch Vertauschen von H und einem Dreieckspunkt entstehen die drei weiteren Dreiecke , die zu dem gleichen Höhenfußpunktdreieck gehören. Harmonische Teilung A´
C
A
Ta
B
Ti
Verlängere BC über C hinaus um AC zu BA´. Zeichne die Winkelhalbierende des Winkels γ und seines Außenwinkels. Du erhältst eine Strahlensatzfigur. Satz: Die Winkelhalbierende eines Winkels und seines Außenwinkels teilen die Gegenseite harmonisch im Verhältnis der anliegenden Seiten. Hilfssatz: Stehen zwei Geraden lotrecht auf einer dritten. So laufen sie parallel. A´
C
A´´
Ta
Beweisfigur für die äußere Teilung‐ A
Ti
B