Blatt 2

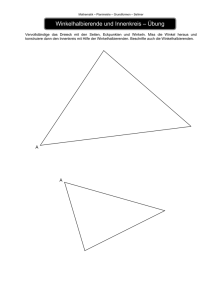
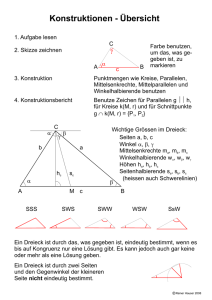
Übungen zur Vorlesung Mathematische Probleme für den Schulunterricht
H. Klein
Blatt 2,27. April 2015
(5) Gegeben sei ein Winkel α gebildet von zwei verschiedenen von einem Punkt A ausgehenden Halbgeraden. Beschreibe eine Methode die Winkelhalbierende von α mit
Zirkel und Lineal zu konstruieren und begründe die Korrektheit dieser Methode.
(6) Sei ∆ = ABC ein Dreieck mit Seiten a, b, c in den Standardbezeichnungen. Bezeichne
F die Fläche von ∆, r den Inkreisradius von ∆ und s den halben Umfang von ∆.
Seien wa die Winkelhalbierende von ∆ durch A und wa0 die äußere Winkelhalbierende
von ∆ durch A und definiere wb , wb0 , wc , wc0 analog. Zeigen Sie:
(a) Sind A0 := wb0 ∩ wc0 , B 0 := wa0 ∩ wc0 und C 0 := wa0 ∩ wb0 die Schnittpunkte
jeweils zweier der äußeren Winkelhalbierenden, so liegen diese jeweils auf der
Winkelhalbierenden durch den dritten Punkt, d.h. A0 ∈ wa , B 0 ∈ wb und
C 0 ∈ wC .
(b) Der Höhenschnittpunkt des Dreiecks ∆0 := A0 B 0 C 0 ist der Mittelpunkt des
Inkreises von ∆.
(c) Der Punkt A0 hat von allen drei Geraden AB, AC, BC denselben Abstand
ra , und entsprechend hat B 0 beziehungsweise C 0 von diesen den gemeinsamen
Abstand rb beziehungsweise rc .
(d) Es sind
ra =
F
F
F
1
1
1
1
, rb =
und rc =
sowie
+ + = .
s−a
s−b
s−c
ra rb rc
r
(7) Sei ∆ = ABC ein Dreieck mit Seiten a, b, c in den Standardbezeichnungen. Bezeichne
D den Schnittpunkt von BC mit der Winkelhalbierenden von ∆ durch A und seien
t := |AN |, p := |CD| und q := |BD|. Zeigen Sie:
(a) Der Punkt D teilt die Seite BC im Verhältnis der anliegenden Seiten, d.h. es
ist p/q = b/c.
(b) Es sind
ac
ab
, q=
und t2 = bc 1 −
p=
b+c
b+c
a
b+c
2 !
.
(8) Sei ∆ ein nicht gleichseitiges Dreieck mit Eulergeraden e. Zeigen Sie das e genau
dann durch eine der Ecken von ∆ läuft wenn ∆ rechtwinklig oder gleichschenklig
ist.
Abgabe: Montag, den 4. Mai bis 1100 im Schrein.