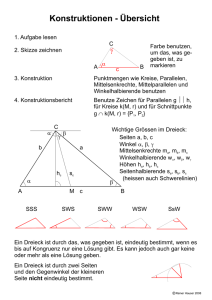
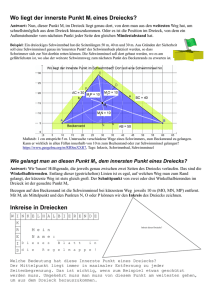
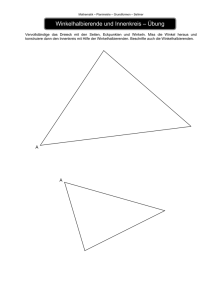
Winkelhalbierende im Dreieck

Winkelhalbierende im Dreieck
•
Bemerkungen für Lehrer:
•
Die Schülerinnen und Schüler kennen den Begriff Winkelhalbierende bereits
und wissen welche Eigenschaft Punkte auf der Winkelhalbierenden haben.
•
Von der Lehrkraft wird ihnen gezeigt,
• wie man ein Dreieck zeichnet,
• wie man Winkel einzeichnet und misst,
• wie man Winkelhalbierende einzeichnet,
• wie man einen Kreis mit vorgegebenem Mittelpunkt und variablem
Radius zeichnet.
•
Selbständig sollen sie in einem Dreieck zwei Winkelhalbierende sowie ihren
Schnittpunkt D einzeichnen. Durch Messung der Teilwinkel von γ
erkennen sie, dass die Verbindungsgerade von D mit der dritten Ecke die
dritte Winkelhalbierende im Dreieck darstellt, d.h. alle drei
Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt
(experimentelles Ergebnis) .
•
Zusätzlich erkennen die Schülerinnen und Schüler durch Einpassen eines
Kreises, dass der gemeinsame Schnittpunkt der Inkreismittelpunkt des
Dreiecks ist. Das Lot von D auf eine der Dreiecksseiten liefert (exakt) den
Inkreisradius, was die Schülerinnen und Schüler auf einem zweiten
Sketchometry-Blatt überprüfen können.
•
Es bleibt dem Lehrer überlassen, anschließend eine mathematische
Begründung für den gemeinsamen Schnittpunkt und den Inkreismittelpunkt
zu liefern.