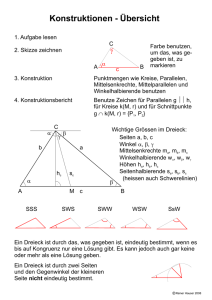
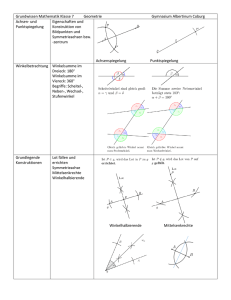
Vorname

Prof.Dr. W.Bley
Dipl.-Math. T.Sprenger
Klausur 02
Klausur zur Vorlesung
ELEMENTARGEOMETRIE
09.10.2007
Name:
Vorname:
Studiengang:
Modularisiert:
ja / nein
Matrikelnummer:
Instruktionen
Legen Sie Ihren Immatrikulationsausweis und Personalausweis sichtbar auf Ihren Schreibtisch! Fullen Sie obige Felder aus! Schreiben Sie auf jeden Zettel Ihren Vor - und Nachnamen!
Bevor Sie anfangen:
Zur Losung einer Aufgabe verwenden Sie bitte den Platz unter der Aufgabenstellung sowie die Ruckseite des
Blattes. Falls der Platz nicht ausreicht, fordern Sie ein neues Blatt an und lassen sie es spater an die Klausur
heften.
Nur vom Korrekteur auszufullen!
Aufgabe 1
(a)
(b)
(c)
Aufgabe 2
Aufgabe 3
Aufgabe 4
Aufgabe 5
SUMME
(a)
(b)
(c)
(a)
(b)
(c)
:
:
:
:
:
:
:
:
:
:
:
:
(2)
(2)
(4)
(4)
(2)
(2)
(1)
(1)
(2)
(1)
(4)
(25)
Name:
Aufgabe 1
Gegeben seien eine Gerade
Vorname:
g mit
g = z 2 R2
und ein Dreieck
z = 4 + 9 ;
3
6
2R
4ABC mit den Punkten
A=
4
0
;
B=
2
3
;
C = 05 :
(a) Bestimmen Sie die Punktrichtungsformen der drei Geraden, die durch Fortsetzung der Seiten des Dreiecks
4ABC entstehen.
(2 Punkte)
(b) Welche Moglichkeiten konnen auftreten? (Mehrfachnennungen moglich)
Eine Gerade und ein Dreieck konnen
keine
einen
drei
unendlich viele
Schnittpunkt(e) besitzen.
Erlautern Sie Ihre Antwort (z.B. anhand einer Zeichnung)!
(c) Berechnen Sie nun alle Schnittpunkte der Geraden
g mit dem Dreieck 4ABC .
zwei
(2 Punkte)
(4 Punkte)
Name:
Vorname:
Aufgabe 2

Gegeben sei ein Fluss mit zwei parallelen Ufern. Uber
diesen Fluss verlauft (senkrecht zum Fluss) eine Brucke
der Lange z = 25 m. Die beiden Teile der Brucke, die sich links und rechts am Ufer benden, sind identisch, d.h.
die unbekannte Lange y der Bruckenenden ist auf beiden Ufern gleich. Ferner existieren drei weitere Punkte A,
B und C . Der Punkt C bendet sich auf der Strecke [AB] und teilt diese in zwei Strecken der Lange v = 7 m
und w = 21 m (siehe Skizze!). Bestimmen Sie die Breite x des Flusses.
(4 Punkte)
Name:
Vorname:
Aufgabe 3
Gegeben seien die beiden Halbgeraden
z = 1 + 1 ;
5
1
h = z 2 R2
2
z = 1 + ;
5
14
g = z 2 R2
2 R+
und
wobei R+ = fx
2 R+ ;
2 R j x 0g.
Die beiden Halbgeraden
g und h schneiden sich unter dem Winkel = \(g; h) in dem Punkt A = 15 .
(a) Bestimmen Siedie Punkte
auf der Halbgeraden
2
6
Ergebnis:
und
:
2
0
p
g und h, deren Abstand zum Punkt A 50 betragt.
(2 Punkte)
(b) Bestimmen Sie nun die Winkelhalbierende des Winkels = \(g; h). (Bedenken Sie, die Winkelhalbierende
ist per denitionem eine Halbgerade!)
(2 Punkte)
(c) Geben Sie unter Verwendung von (b) die Winkelhalbierende des Winkels
= \(h; g ) an.
(1 Punkt)
Name:
Vorname:
Aufgabe 4
In dem Modell von Poincare und in dem Modell von Klein gilt das Axiom:
Zu zwei verschiedenen Punkten
A und B existiert genau eine Gerade g mit A; B 2 g .
Beschreiben Sie jeweils in Worten die Konstruktion der durch die beiden gegebenen Punkte A und B eindeutig
bestimmten Geraden g . Verdeutlichen Sie die Konstruktion jeweils anhand der Skizze.
(a) Poincare-Modell
(1 Punkt)
(b) Poincare-Modell
(2 Punkte)
(c) Kleinmodell
(1 Punkt)
Name:
Vorname:
Aufgabe 5
Beweisen Sie fur das Dreieck
4ABC :
Das Dreieck ist gleichschenklig mit
a = b () Die Winkel und sind gleich gro
(4 Punkte)
Hinweis:
)\: Betrachten Sie die Winkelhalbierende von und verwenden Sie die Kongruenzsatze.
(\: Betrachten Sie die Winkelhalbierende von , zeigen Sie = 90 und verwenden Sie die Kongruenzsatze.
"
"