to the PDF file.

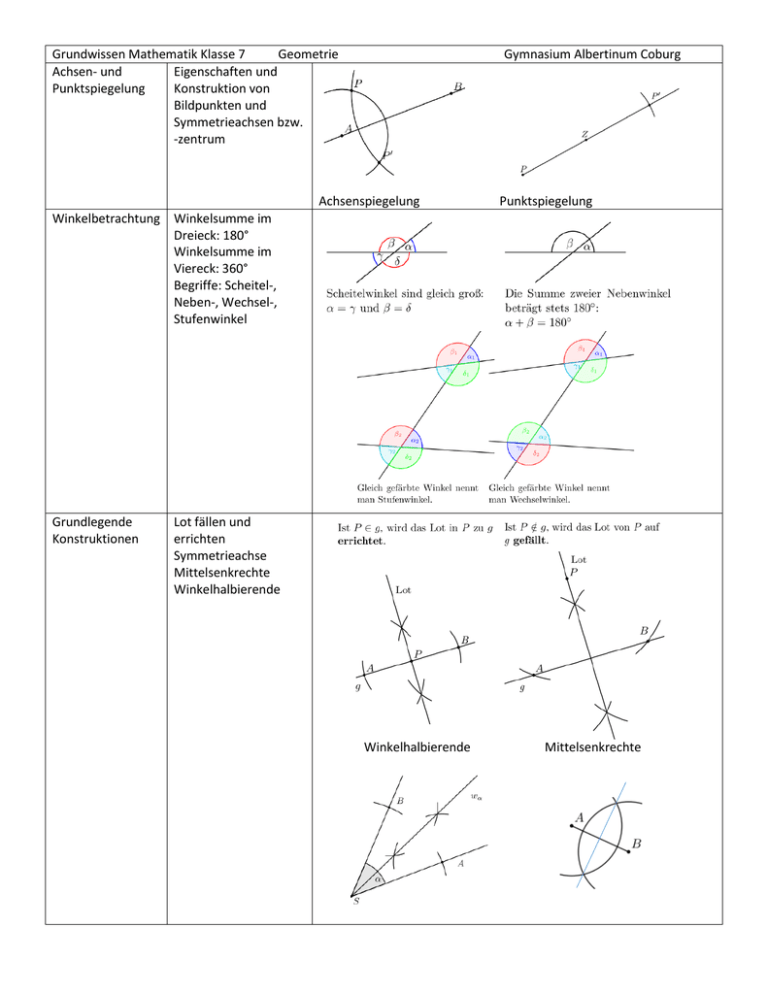
Grundwissen Mathematik Klasse 7
Geometrie
Achsen- und
Eigenschaften und
Punktspiegelung
Konstruktion von
Bildpunkten und
Symmetrieachsen bzw.
-zentrum
Gymnasium Albertinum Coburg
Achsenspiegelung
Punktspiegelung
Winkelbetrachtung Winkelsumme im
Dreieck: 180°
Winkelsumme im
Viereck: 360°
Begriffe: Scheitel-,
Neben-, Wechsel-,
Stufenwinkel
Grundlegende
Konstruktionen
Lot fällen und
errichten
Symmetrieachse
Mittelsenkrechte
Winkelhalbierende
Winkelhalbierende
Mittelsenkrechte
Vierecke
Raute, Drachenviereck,
Parallelogramm,
Trapez
und ihre Eigenschaften
Besondere
Dreiecke und
deren
Eigenschaften
spitzwinklig,
rechtwinklig,
stumpfwinklig
gleichschenklig,
gleichseitig
Linien im Dreieck
Winkelhalbierende
(Inkreis)
Höhe
Mittelsenkrechte
(Umkreis)
Thaleskreis
Erkennung und
Konstruieren von
rechtwinkligen
Dreiecken
Dreieck ABC ist rechtwinklig, wenn C auf dem Thales(halb-)kreis liegt.
Kongruenz
(insbesondere von
Dreiecken)
Erkennen von
Kongruenz
(Deckungsgleichheit):
Bei Übereinstimmung
in 3 entsprechenden
„Stücken“
Konstruktion von
(meist eindeutig
festgelegten)
Dreiecken
Kongruenzsätze: SSS, SWS, WSW, SWW, SsW
Zwei Kongruente Dreiecke
Grundwissen Mathematik Klasse 7
Algebra
Terme
Potenzen mit natürlichem Exponenten
Klammerregeln
Multiplizieren von Summen
Zusammenfassen von Termen
(Gleichartige Terme dürfen addiert/
subtrahiert werden)
Gymnasium Albertinum Coburg
𝑎 ⋅ 𝑎7 = 𝑎3+7 = 𝑎10
2𝑥 − (2𝑦 + 𝑥) = 2𝑥 − 2𝑦 − 𝑥 = 𝑥 − 2𝑦
(2𝑥 + 3) ⋅ (𝑦 − 𝑥) = 2𝑥𝑦 − 2𝑥 2 + 3𝑦 − 3𝑥
3𝑎 + 4𝑥 + 5𝑎 = 8𝑎 + 4𝑥
4𝑚 + 2𝑚2 + 3𝑚 = 7𝑚 + 2𝑚2
3
𝑇(𝑥; 𝑦) = (𝑥 2 + 3): 2 ⋅ 𝑥 − 𝑦
𝑇(5; 3) = (52 + 3): 2 ⋅ 5 − 3 = 28: 2 ⋅ 5 − 3
= 14 ⋅ 5 − 3 = 70 − 3 = 67
Berechnen von Termwerten
Umformungen
 Ausmultiplizieren
 Ausklammern/ Faktorisieren
2𝑥(𝑥 − 3𝑦 + 5𝑥𝑦) = 2𝑥 2 − 6𝑥𝑦 + 10𝑥 2 𝑦
8𝑥 4 + 6𝑥 3 − 4𝑥 2 = 2𝑥 2 (4𝑥 2 + 3𝑥 − 2)
Aufstellen und Interpretieren von Sichtbare Seiten beim Würfelturm
Termen
Gleichungen
Lösungsverfahren
Diagramme
Interpretieren
5𝑥 + 7 = 2 − 3𝑥 | + 3𝑥
8𝑥 + 7 = 2
| −7
8𝑥
= −5
| ∶8
𝑥
= −5: 8
𝑥
= −0,625
und
Auswerten


Rechenwerkzeug Anwendung
auf
Dreisatz
Problemstellungen
(Grundlagen der
6. Klasse)
3
4
𝑥=6
| ⋅
4
3
4
𝑥 =6⋅3=8
Auswerten von Daten
z. B. rot 24
insgesamt 120
Prozentualer Anteil von „rot“
24
1
20
= = 0,2 = 0,20 =
= 20%
120 5
100
verschiedene z. B. Wie viel Grad hat der Mittelpunktswinkel für den Anteil „silber“ in
einem Kreisdiagramm?
120 Autos =
̂ 360°
1 Auto =
̂ 360°: 120 = 3°
48 Autos =
̂ 3° ⋅ 48 = 144°
Wie viel Prozent sind „silber“? Wie viel Grad entspricht das?
Prozentwert = Prozentsatz⋅Grundwert
48 =
𝑝 ⋅ 120
⇒ 𝑝 = 48: 120 = 0,40 = 40%
𝑥=
0,40 ⋅ 360° = 144°
Grundgleichung
Veränderung des Grundwertes
der
Prozentrechnung
Ein Fahrrad kostet 100€. Zunächst wird der Preis wegen einer
Rabattaktion um 20% reduziert. Am Ende der Rabattaktion wird der
reduzierte Preis um 20% erhöht. Wie viel kostet das Fahrrad nun?
100€ − 0,2 ⋅ 100€ = 80€ (Preis nach Rabattabzug)
20% von 80€ = 16€ (Neuen Grundwert beachten!)
80€ + 16€ = 96€ (Preis nach 20% Erhöhung)