K7 Geometrie
Werbung

Slide 1
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
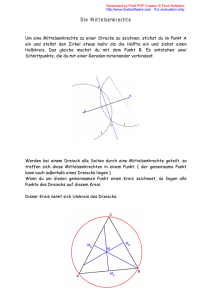
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 2
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 3
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 4
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 5
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 6
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 7
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 8
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 9
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 10
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 11
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 2
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 3
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 4
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 5
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 6
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 7
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 8
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 9
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 10
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt
Slide 11
Transversalen im Dreieck
Transversalen sind besondere Linien im Dreieck
man unterscheidet dabei diese 4 Arten:
Mittelsenkrechte
Winkelhalbierende
Seitenhalbierende
Höhe
Inhalt
Mittelsenkrechte und Umkreis
Winkelhalbierende und Inkreis
Definition
Eigenschaften
Höhe
Definition
Eigenschaften
Inkreis
Seitenhalbierende und Schwerpunkt
Definition der Mittelsenkrechten
Eigenschaften der Mittelsenkrechten
Umkreis
Definition
Eigenschaften
Überblick
Zurück zum Inhalt
Mittelsenkrechte
mAB
A
Auf der Mittelsenkrechten der
Strecke [AB] liegen alle Punkte,
die von A und B gleichweit
entfernt sind.
Jeder Punkt der
Mittelsenkrechte ist der
Mittelpunkt eines Kreises,
der durch A und B geht.
B
Zurück zum Inhalt
Eigenschaften der Mittelsenkrechte
Die Mittelsenkrechte
Geht durch die Mitte der Strecke
Steht senkrecht auf der Strecke
Ist Symmetrieachse der beiden Punkte
Ist Symmetrieachse der Strecke
Zurück zum Inhalt
Der Umkreis eines Dreiecks
C
Der Schnittpunkt M der
beiden Mittelsenkrechten
mAB und mAC ist einerseits
von A und B gleichweit
entfernt, anderseits aber
auch von A und C.
mAB
mAC
Also ist M auch von B und
C gleichweit entfernt. Die
Mittelsenkrechte mBC geht
also auch durch M.
M
M ist also der Mittelpunkt
des Kreises durch A, B
und C. Dieser Kreis ist der
Umkreis des Dreiecks
ABC.
A
mBC
B
Zurück zum Inhalt
Winkelhalbierende
w
Auf der Winkelhalbierenden
w des Winkels liegen alle
Punkte die von den beiden
Schenkeln des Winkels
gleiche Abstände haben.
Jeder Punkt der
Winkelhalbierenden ist der
Mittelpunkt eines Kreises,
der die beiden Schenkel a
und b berührt
b
A
c
Zurück zum Inhalt
Eigenschaften der Winkelhalbierenden
Die Winkelhalbierende
Geht durch den Scheitelpunkt des Winkels
Halbiert das Winkelfeld
Ist Symmetrieachse der beiden Schenkel
Ist Symmetrieachse des Winkelfeldes
Zurück zum Inhalt
Der Inkreis im Dreieck
C
Der Schnittpunkt O der
beiden Winkelhalbierenden
w und w ist einerseits von
b und c gleichweit entfernt,
anderseits aber auch von a
und c.
w
a
w
b
O ist also der Mittelpunkt
des Kreises, der c, b und
a berührt.
Dieser Kreis ist der
Inkreis des Dreiecks
ABC.
O
A
c
w
Also ist O auch von a und
b gleichweit entfernt. Die
Winkelhalbierende w
geht also auch durch O.
B
Zurück zum Inhalt
Die Seitenhalbierenden im Dreieck
C
sc
Ma
S
Mb
sb
sa
B
Die Seitenhalbierenden gehen
jeweils durch einen Eckpunkt
und den Mittelpunkt der
gegenüberliegenden Seite.
Die Seitenhalbierenden sa, sb
und sc schneiden sich im
Schwerpunkt S des Dreiecks.
(Physikalische Bedeutung:
Punkt, auf dem man das
Dreieck balancieren kann.)
Daher nennt man die
Seitenhalbierenden auch
Schwerlinien.
Mc
A
Zurück zum Inhalt
Die Höhen im Dreieck
C
hc
ha
H
A
hb
Die Höhen gehen jeweils
durch einen Eckpunkt und
stehen auf der gegenüberliegenden Seite
senkrecht.
Die Höhen ha, hb und hc
schneiden sich im
Höhenschnittpunkt H, der
keine besondere geometrische
Bedeutung hat.
B
Zurück zum Inhalt
Eigenschaften der Transversalen im
allgemeinen Dreieck
Geht durch den
Eckpunkt
Mittelsenkrechte
Seitenhalbierende
ja
Höhe
ja
Winkelhalbierende
ja
Geht durch den
Seitenmittelpunkt
Steht auf der
Seite senkrecht
ja
ja
Halbiert den
Winkel
ja
ja
ja
Zurück zum Inhalt