Station 1: Mittelsenkrechte und Winkelhalbierende

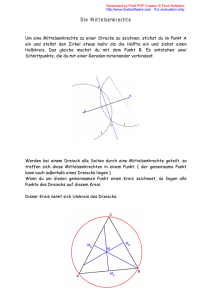
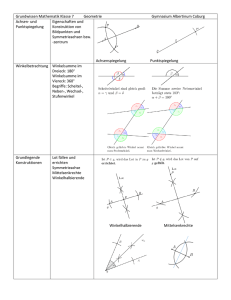
Station 1: Mittelsenkrechte und Winkelhalbierende
Regel
Definition Mittelsenkrechte:
- ist die Symmetrieachse einer Strecke AB
- alle Punkte auf der Mittelsenkrechten haben den gleichen Abstand von den
Punkten A und B
- Mittelsenkrechten von Kreissehnen schneiden sich im Kreismittelpunkt.
Konstruktion:
Die Mittelsenkrechte kann mit Hilfe des Geodreiecks (Strecke abmessen ->
Mitte bestimmen -> Gerade im 90-Grad-Winkel dort einzeichnen) gezeichnet
werden. Alternativ ist die Konstruktion mit dem Zirkel möglich (-> Lehrer
fragen).
Regel:
Definition Winkelhalbierende:
- Ist die Symmetrieachse eines Winkels
- Alle Punkte der Winkelhalbierenden haben von den Schenkeln den
gleichen Abstand
Konstruktion:
Kreisbogen um den Winkel -> zwei gleichgroße Kreisbögen um den
Schnittpunkt des ersten Kreisbogens mit den Schenkeln -> Schnittpunkt mit
dem Winkel verbinden
Aufgaben:
1. Teile mit Lineal und Zirkel die Strecke AB =
10,2 cm in zwei gleich große Teile.
2. Zeichne einen Winkel von α=60 Grad und teile
ihn in zwei gleich große Winkel.
3. Zeichne das Dreieck A(1/3), B(7/8) und
C(2/10).
a) Konstruiere die Mittelsenkrechte von AB.
b) die Symmetrieachse von AC.
c) Teile den Winkel BCA.
H.A.: S. 104/5, 7 und S. 105/13, 19
Dr. Martens