Vortrag

Klassenstufe 7
Planung einer Unterrichtsstunde mit DGS
Lisa Knörzer
Vorbereitungsseminar Mathematik zum fachdidaktischen Blockpraktikum (2007)
Dozentin: Frau Homberg-Halter
Verlauf der Sitzung
• Vortrag:
– Präsentationsmodi nach Bruner
– Beispielaufgabe: Satz des Thales
– Thema: Besondere Linien im Dreieck
• Arbeitsphase:
– Erstellen von Arbeitsaufträgen
– Ausführen und Kommentieren der Arbeitsaufträge
• Präsentation der Ergebnisse und Diskussion
Präsentationsmodi nach Bruner
Beschreiben die kognitive Repräsentation von Wissen
• Enaktiv
der handelnde Zugang
• Ikonisch
der bildliche Zugang
• Symbolisch
Darstellung mithilfe von Zeichen
Beispiel: enaktiv
• Gärtnerkonstruktion einer Ellipse
• Befestige zwei Klammern auf einer Karteikarte.
• Befestige die beiden Enden des Fadens an den beiden Klammern.
• Ziehe mit einem Stift den Faden stramm und führe den Stift um
die Klammern herum
http://www.informatik.uni-bremen.de/~shahn/kegelschnitte/text/durch
fuehrung/stunden1/stunden1.htm
Beispiel: ikonisch
• Ellipse: Darstellung mit Euklid DynaGeo
Beispiel: symbolisch
Aus Skript zur VL Kegelschnitte WS 09
Hieraus möglich: Herleitung der allgemeinen
2
Ellipsengleichung
2
x
y
+ 2 =1
2
a
b
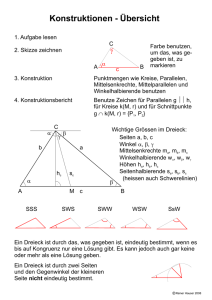
Beispielaufgabe: Satz des Thales
1. Im Zuschauerraum eines Theater sollen alle Zuschauer einen
Platz erhalten, sodass der entsprechende Sehwinkel überall
gleich groß ist. Der Sehwinkel ist der Winkel zwischen den
beiden Bühnenecken und dem Zuschauer.
2. Platziere die Zuschauer nun so, dass der Raum optimal
ausgenutzt wird.
Beispielaufgabe: Satz des Thales
Ausgangslage
Lösung von Aufgabe 2
Mögliche Lösung von Aufgabe 1
Besondere Linien im Dreieck
http://www.saarland.de/dokumente/thema_bildung/mathematik7.pdf
Besondere Linien im Dreieck
• Lernvoraussetzungen:
– Grundbegriffe: Eigenschaften von Dreiecken
(z. B. gleichschenklig)
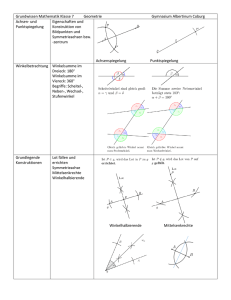
– Grundbegriffe: Mittelsenkrechte, Winkelhalbierende
– Umgang mit Euklid DynaGeo
Mittelsenkrechte
• Definition:
„Die Mittelsenkrechte einer Strecke AB enthält
genau die Punkte P, die jeweils von A und von B
dieselbe Entfernung haben:
{P | |AP| = |BP|} = Mittelsenkrechte von AB“
Krauter: Erlebnis Elementargeometrie, S. 67
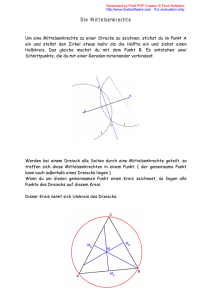
Mittelsenkrechte
Mittelsenkrechten im Dreieck
• Sie schneiden sich in einem Punkt U, das ist
der Umkreismittelpunkt des Dreiecks.
Welche Eigenschaft hat dieser Punkt in Bezug
zu den drei Eckpunkten des Dreiecks?
Winkelhalbierende
• Definition:
„Die Winkelhalbierende eines Winkels mit den
Schenkeln a und b enthält genau die Punkte P, die
jeweils von a und von b denselben Abstand haben:
{ P | Abstand (P, a) = Abstand (P, b) } = Winkelhalbierende des Winkels (a, b).“
Krauter: Erlebnis Elementargeometrie, S. 69
Winkelhalbierende
Winkelhalbierende im Dreieck
• Sie schneiden sich in einem Punkt I, das ist der
Inkreismittelpunkt des Dreiecks.
Welche Eigenschaft hat dieser Punkt in Bezug
auf die drei Seiten des Dreiecks?
Aufgaben
a)
Zeichnet Mittelsenkrechte und Winkelhalbierende als Ortslinie mithilfe
von Euklid DynaGeo.
(Das heißt, ohne Anwendung der direkten Befehle!)
b)
Entwickelt Arbeitsaufträge für Schüler, sodass
1.
2.
die Winkelhalbierende und
die Mittelsenkrechte
als Ortslinie von den Schülern entdeckt werden.
c) Erstellt Arbeitsaufträge für Schüler, sodass die Eigenschaften
3.
4.
der Winkelhalbierenden
der Mittelsenkrechten
auf das Dreieck übertragen werden.
( Entdeckung des In-/Umkreismittelpunktes)
d) Bearbeitet die gestellten Aufträge einer anderen Gruppe und
kommentiert diese.