Lösung TD

Einführung in die Energietechnik
Tutorium II: Thermodynamik
1 Thermodynamik allgemein
1.1
• offenes System: kann Materie und Energie mit der Umgebung austauschen.
• geschlossenes System: kann nur Energie mit der Umgebung austauschen.
• abgeschlossenes System: kann weder Materie noch Energie austauschen.
1.2
• intensive Zustandsgrößen: sind unabhängig von der betrachteten Stoffmenge, z.B. Druck p, Temperatur T.
• extensive Zustandsgrößen: sind abhängig von der Stoffmenge, z.B. Volumen V, innere Energie U.
1.3
Das ideale Gasgesetz ist Ausgangspunkt für die Betrachtung aller Zustandsänderungen.
m
p · V = |n{z
· R} ·T =
·R·T
M
=const.
p·
V
R
·T
=
m
M
|{z}
|{z}
=V ∗
=RS
RS heißt spezifische Gaskonstante. Im folgenden wird der Variablenname V für
das massebezogene Volumen verwendet.
p · V = RS · T
Isotherme Zustandsänderung:
T = const. ⇒ p · V = const.
∆S = (cp − cV ) · ln
V2
V1
1
1.4 Einführung in die Energietechnik
Tutorium II: Thermodynamik
wobei für die Differenz der Wärmekapazitäten gilt: cp − cV = RS
Bleibt die Temperatur konstant, so gilt dies auch für die innere Energie U (⇒
dU = 0).
⇒ Q = −Wt = −WV
Isobare Zustandsänderung:
p = const. ⇒
V
= const.
T
∆S = cp · ln
T2
T1
Q = cp · (T2 − T1 )
Isochore Zustandsänderung:
V = const. ⇒
p
= const.
T
∆S = cV · ln
T2
T1
Q = cV · (T2 − T1 )
Adiabate Zustandsänderung:
p · V κ = const.
wobei für den Adiabatenexponent gilt: κ = ccVp
Sie wird auch isentrope Zustandsänderung genannt, d.h. ∆S = 0.
Mit der Umgebung wird keine Wärmeenergie ausgetauscht (Q = 0).
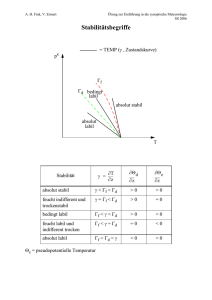
Diagramme: siehe Abbildung 1
1.4
Bei der adiabaten Ausdehnung findet kein Temperaturausgleich mit der Umgebung statt, das Gas kühlt sich ab. Daher sinkt der Druck stärker als bei der isothermen Expansion.
2
1.5 Einführung in die Energietechnik
Tutorium II: Thermodynamik
Abb. 1: p-V- und T-S-Diagramme
1.5
Die Enthalpie ist folgendermaßen definiert:
H=
U
|{z}
+
innere Energie
p·V
| {z }
Arbeitsfähigkeit
Somit gilt für infinitesimale Änderungen:
dH = dU + p · dV + V · dp
dH = T · dS +
V · dp
| {z }
Term für technische Arbeit
Weiterhin gilt:
T · dS = dU + p · dV
dU = dQ + dW
(Definition der Entropie)
(1. Hauptsatz Thermodynamik)
1.6
Die technische Arbeit Wt wird manchmal auch als „technisch nutzbare Arbeit“
bezeichnet.
Z 2
Wt =
V · dp
1
3
1.7 Einführung in die Energietechnik
Tutorium II: Thermodynamik
Abb. 2: Kolbenmodell für die Volumenänderungsarbeit
Betrachtet man einen Kolben, der mit Gas des Druckes p gefüllt ist, so ergibt sich
die Volumenänderungsarbeit aus der Newton’schen Definition.
Z
Z
~
~
W = F · ds = p · A
· ds}
| {z
dV
Durch das Minuszeichen wird nur noch definiert, dass vom System abgegebene
Energie negativ angegeben wird. Die Formel für die Volumenänderungsarbeit
WV lautet also:
Z
2
WV = −
p · dV
1
Berechnet man technische oder Volumenänderungsarbeit für einen ganzen Kreisprozeß, so erhält man dasselbe Ergebnis für die verrichtete Arbeit (man berechnet dieselbe Fläche im p-V-Diagramm). Für einzelne Zustandsübergänge ergeben
sich jedoch unterschiedliche Werte!
1.7
p·V
WV
= const. = p1 · V1
Z 2
Z
= −
p · dV = −p1 V1 ·
2
1
dV =
1
1 V
V2
= −p1 V1 (ln V2 − ln V1 ) = −p1 V1 ln
V1
4
1.8 Einführung in die Energietechnik
Tutorium II: Thermodynamik
1.8
„Polytrope Zustandsänderung“ ist die allgemeine Bezeichnung für jede Zustandsänderung, für die gilt:
p · V n = const.
Je nach Wert des Polytropenexponentes n können auch die unter 1.3. betrachteten
Zustandsübergänge (Sonderfälle) dargestellt werden:
n
n
n
n
=
=
=
→
0 isobar
1 isotherm
κ adiabat
∞ isochor
pV n = p1 V1n
Z 2
Z 2
WV = −
p · dV = −
p1 V1n · V −n · dV =
1
1
·
¸2
1
n
1−n
=
= −p1 V1
·V
1−n
1
¡
¢
1
=
p1 V1n V21−n − V11−n =
n−1 

=
1 
p1 V n V −n ·V2 − p1 V1n V11−n  =
| {z }
n − 1 | 1{z 2 }
=p2
=
=V1
1
(p2 V2 − p1 V1 )
n−1
1.9
Z
Wt =
2
Z
2
1
−1
V dp =
p1n V1 · p n dp =
1
1
·
¸2
1
1
1
1− n
n
= p1 V1
·p
=
1 − n1
1
´
1
n ³ n1
1− 1
1− 1
p1 V1 p2 n − p1n V1 p1 n =
=
n−1
n
=
(p2 V2 − p1 V1 )
n−1
5
Einführung in die Energietechnik
Tutorium II: Thermodynamik
2 Carnot-Prozeß
Ein Carnot-Prozeß besteht aus folgenden Zustandsänderungen:
- isotherme Expansion (bei TH = 420K)
- adiabatische Expansion (unter Abkühlung)
- isotherme Kompression (bei TK = 300K)
- adiabatische Kompression (unter Erwärmung)
2.1
p
T
1
1
adiabatisch
h
tis c
aba
adi
the
rm
2
ad
b
ia
h
i sc
at
4
is ot
he r
m
isotherm
4
2
adiabatisch
iso
isotherm
3
3
V
S
Abb. 3: Carnot-Prozeß im p-V- und T-S-Diagramm
2.2
Ansatz: Polytrope Zustandsänderung idealer Gase (aus Formelsammlung)
T2
=
T1
µ
p2
p1
¶ n−1
n
Mit n = κ = 1, 4 für die adiabatische Zustandsänderung folgt:
κ
µ ¶ κ−1
T2
p2 = p1
T1
κ
µ ¶ κ−1
T3
= 1, 08bar
p3 = p2 ·
T2
6
2.3 Einführung in die Energietechnik
µ
p4 = p1 ·
T4
T1
Tutorium II: Thermodynamik
κ
¶ κ−1
= 1, 85bar
Für die nachfolgende Teilaufgabe werden gleich noch die Volumina berechnet.
V =
p
T
V
1
6bar
420K
3
0, 201 m
kg
RS · T
p
2
3,5bar
420K
3
0, 344 m
kg
3
1,08bar
300K
3
0, 799 m
kg
4
1,85bar
300K
3
0, 467 m
kg
2.3
isotherme Expansion 1 → 2
Z
2
Wt12 = −
pdV = −p1 · V1 · ln(
1
( = RS · T1 · ln(
= −65
V2
)
V1
p2
)
p1
)
kJ
kg
(da isotherm)
kJ
kg
Q12 = −Wt12 = 65
adiabatische Expansion 2 → 3
Z
3
Wt23 =
V dp =
2
1
· (p3 · V3 − p2 · V2 )
n−1
1
· (RS · T3 − RS · T2 ) )
n−1
kJ
= −119
kg
= 0 (da adiabatisch)
( =
Q23
7
2.4 Einführung in die Energietechnik
Tutorium II: Thermodynamik
isotherme Kompression 3 → 4
Z
4
Wt34 = −
pdV = −p3 · V3 · ln(
3
( = RS · T3 · ln(
= 46, 4
p4
) )
p3
V4
)
V3
kJ
kg
Q34 = −Wt34 = −46, 4
kJ
kg
(da isotherm)
adiabatische Kompression 4 → 1
Z
1
V dp =
Wt41 =
4
( =
( =
( =
=
Q23 =
1
· (p1 · V1 − p4 · V4 )
n−1
1
· (RS · T1 − RS · T4 ) )
n−1
1
· (RS · T2 − RS · T3 ) )
n−1
−Wt23 )
kJ
119
kg
0 (da adiabatisch)
Verwendet man die in Klammern angegebenen Umformungen, so kann auf die
Berechnung der Volumina unter Teilaufgabe 2 verzichtet werden.
X
kJ
kJ
kJ
kJ
kJ
− 119
+ 46, 4
+ 119
= −18, 6
kg
kg
kg
kg
kg
X
kJ
kJ
kJ
kJ
kJ
Q = 65, 0
+0
− 46, 6
+0
= 18, 6
kg
kg
kg
kg
kg
Wt = −65, 0
2.4
Der thermische Wirkungsgrad ergibt sich aus dem Verhältnis von verrichteter
Arbeit zu aufgenommener Wärmeenergie.
P
18, 6
| Wt |
=
= 28, 6%
ηtherm =
Qzu
65
8
Einführung in die Energietechnik
Tutorium II: Thermodynamik
Der (nur theoretisch funktionierende) Carnotprozess hat den maximal möglichen
Wirkungsgrad, der bei gegebenen Temperaturen von kaltem und heißem Wärmereservoir denkbar ist.
Th − Tk
ηCarnot =
(hier = 28, 6%)
Th
3 Joule-Prozeß
Der Joule-Prozeß wird aus folgenden Teilen gebildet:
- adiabatische Kompression (unter Erwärmung)
- isobare Expansion (unter Erwärmung)
- adiabatische Expansion (unter Abkühlung)
- isobare Kompression (unter Abkühlung)
3.1
p
T
3
a
ob
is
h
sc
a ti
iab
ad
ch
atis
isobar
2
adiabatisch
ab
adi
1
r
4
1
4
adiabatisch
2 isobar
3
iso
bar
V
S
Abb. 4: Joule-Prozeß im p-V- und T-S-Diagramm
3.2
Zur Berechnung der fehlenden Temperaturen verwenden wir wieder die Gleichung für den adiatischen Übergang
µ ¶ κ−1
T2
p2 κ
=
T1
p1
9
3.3 Einführung in die Energietechnik
µ
⇒ T2 = T1 ·
µ
⇒ T4 = T3 ·
p2
p1
p4
p3
Tutorium II: Thermodynamik
¶ κ−1
κ
¶ κ−1
κ
= 506K
= 553K
Damit ergibt sich die vollständige Wertetabelle zu:
1
1bar
303K
3
0, 870 m
kg
p
T
V
2
6bar
506K
3
0, 242 m
kg
3
6bar
923K
3
0, 442 m
kg
4
1bar
553K
3
1, 59 m
kg
3.3
adiabatische Kompression 1 → 2
κ
kJ
· (p2 · V2 − p1 · V1 ) = 203, 7
κ−1
kg
= 0 (da adiabatisch)
Wt12 =
Q12
isobare Expansion 2 → 3
Z
3
Wt23 =
V dp = 0
(da p=const.)
2
Q23 = cp · (T3 − T2 ) = 419
kJ
kg
adiabatische Expansion 3 → 4
κ
kJ
· (p4 · V4 − p3 · V3 ) = −371, 7
κ−1
kg
= 0 (da adiabatisch)
Wt34 =
Q34
isobare Kompression 4 → 1
Z
3
Wt41 =
V dp = 0
(da p=const.)
2
Q41 = cp · (T1 − T4 ) = −251
kJ
kg
10
3.3 Einführung in die Energietechnik
X
Tutorium II: Thermodynamik
kJ
kJ
kJ
kJ
kJ
+0
− 371, 7
+0
= −168
kg
kg
kg
kg
kg
X
kJ
kJ
kJ
kJ
kJ
Q = 0
+ 419
+0
− 251
= 168
kg
kg
kg
kg
kg
P
| Wt |
168
ηtherm =
=
= 40%
Qz u
419
Wt = 203, 7
Zum Vergleich: Der Carnot-Prozeß hätte bei diesen Temperaturgrenzen einen
Wirkungsgrad von 67%.
ηCarnot = 1 −
303K
= 67%
923K
11