Zustandsänderungen in der Atmosphäre

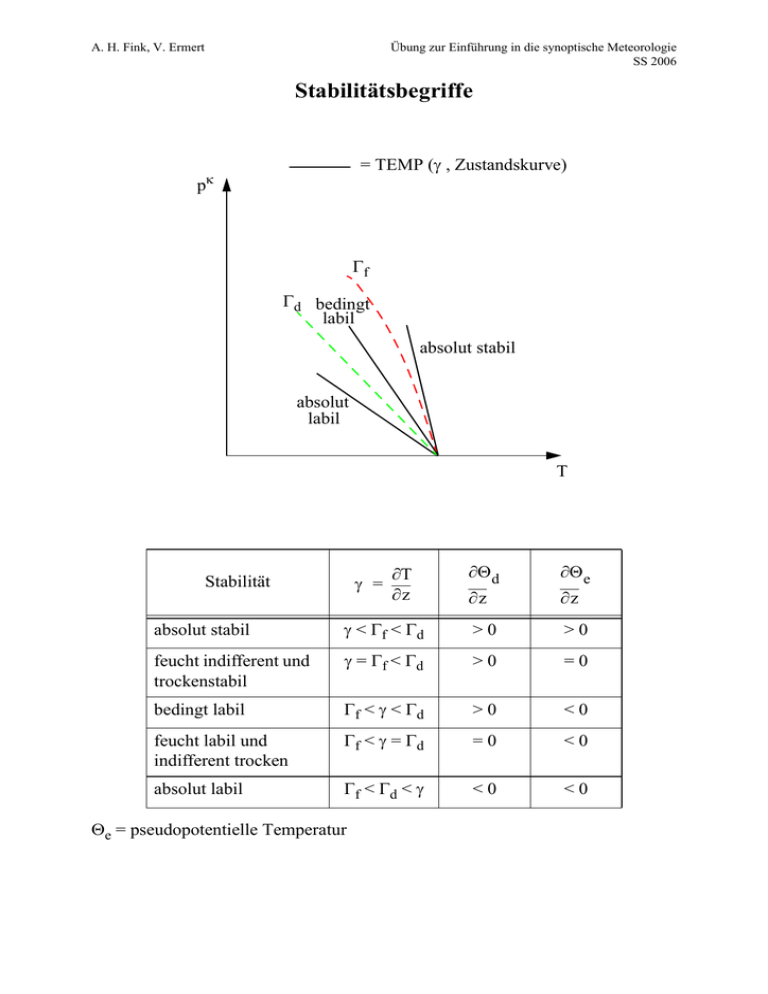
A. H. Fink, V. Ermert
Übung zur Einführung in die synoptische Meteorologie
SS 2006
Stabilitätsbegriffe
= TEMP (γ , Zustandskurve)
κ
p
Γf
Γd bedingt
labil
absolut stabil
absolut
labil
T
γ =
Stabilität
∂T
∂z
∂Θ d
∂Θ e
∂z
∂z
absolut stabil
γ < Γf < Γd
>0
>0
feucht indifferent und
trockenstabil
γ = Γf < Γd
>0
=0
bedingt labil
Γf < γ < Γd
>0
<0
feucht labil und
indifferent trocken
Γf < γ = Γd
=0
<0
absolut labil
Γf < Γd < γ
<0
<0
Θe = pseudopotentielle Temperatur
A. H. Fink, V. Ermert
Übung zur Einführung in die synoptische Meteorologie
SS 2006
Zustandsänderungen
• adiabatisch
Adiabatisch wird eine Zustandsänderung genannt, wenn das betrachtete Luftpaket keinen thermischen
Kontakt mit seiner Umgebung hat, d. h. es darf weder zum Austausch von sensibler Wärme noch der
im Wasserdampf enthaltenen Kondensationsenergie (wird als latente Wärme bezeichnet) mit der Umgebung kommen.
• trockenadiabatisch
Eine Zustandsänderung eines Luftpakets wird als trockenadiabatisch bezeichnet, wenn keine sensible
oder latente Wärme zu- oder abgeführt wird und die im Wasserdampf latent vorhandene Energie nicht
freigesetzt wird. D. h. es handelt sich um die adiabatische Zustandsänderung eines Luftpakets bei
der keine Kondensation des Wasserdampfs auftritt.
• feuchtadiabatisch
Die Zustandsänderung des Luftpakets ist feuchtadiabatisch, wenn sie adiabatisch ist und das Luftpaket
bei Sättigung seine latente Wärme durch Kondensation freisetzt. Damit handelt es sich um die adiabatische Zustandsänderung eines Luftpakets unter Berücksichtigung der Phasenübergänge des Wassers.
•
trockenadiabatischer Temperaturgradient
Der trockenadiabatische Temperaturgradient kann aus dem 1. Hauptsatz der Thermodynamik hergeleitet
werden (dQ=0):
( c p dT – αdp = dQ = 0 )
⇔
dp
 c dT
------- = α ------
 p dz
dz
Es folgt mit der hydrostatischen Grundgleichung ( dp = – ρgdz
dT
g
Γ d ≡ ------- = – ----dz
cp
) und
1
α ≡ --ρ
:
Damit ist der trockenadiabatische Temperaturgradient lediglich abhängig von der
Erdbeschleunigung (g) und der spezifischen Wärmekapazität bei konstantem Druck (cp). Unter
Vernachlässigung der Höhenabhängigkeit der Erdbeschleunigung ist er damit höhenkonstant.
Für den trockenadiabatischen Temperaturgradient lässt sich der Zusammenhang zwischen Temperatur
R
- ≈ 0,286
und Druck aus dem ersten Hauptsatz, die allgemeinte Gasgleichung p = ρRT und mit κ ≡ ---cp
herleiten:
ρ
RT dp dT
R dp
c p dT = αdp ⇔ dT = ----- dp = -------- ------ ⇔ ------- = ----- ------ ⇔ d ln T = κ d ln p
cp
cp p
T
cp p
a
Durch Integration ergibt sich durch ln a – ln b = ln --b- und a b = exp ( b ln a ) die sog. "Poisson-Gleichung":
p κ
T
------ =  -----
p 
T0
0
Falls p0=1000 hPa, dann ergibt sich per Definition für die potenzielle Temperatur (θ):
1000 hPa κ

θ ≡ T ---------------------

p
Beachte: [T]=K