1. Klausur in "Technischer Thermodynamik I"
Werbung
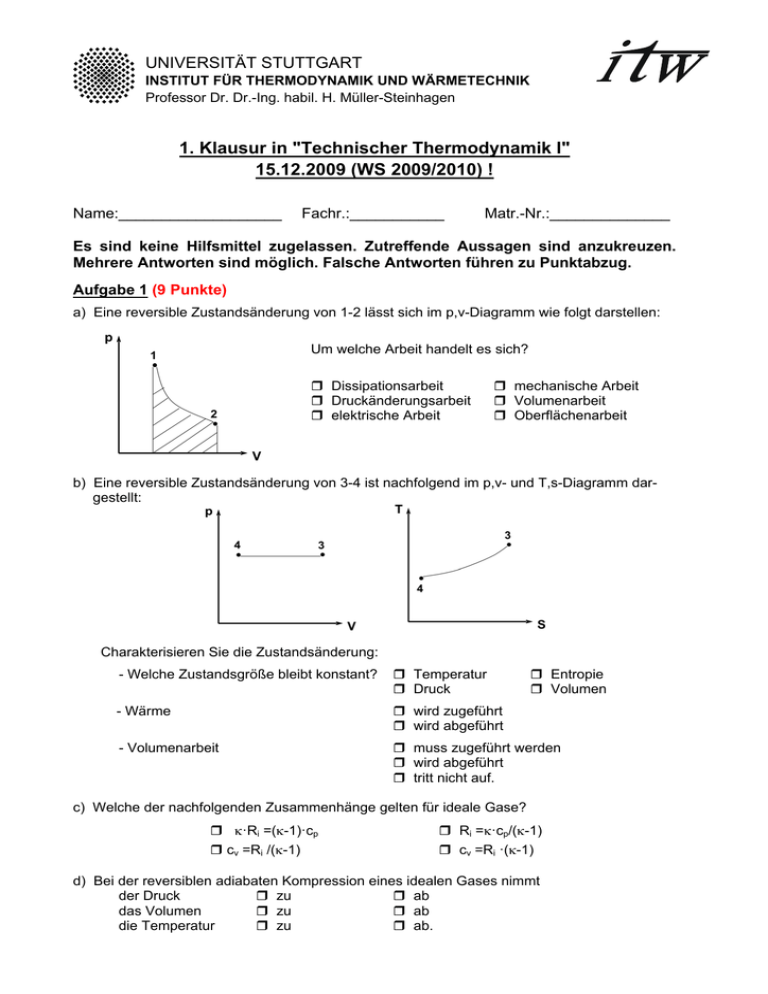
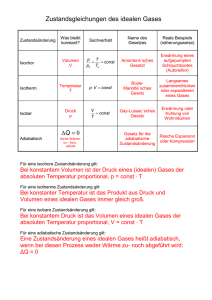
UNIVERSITÄT STUTTGART INSTITUT FÜR THERMODYNAMIK UND WÄRMETECHNIK Professor Dr. Dr.-Ing. habil. H. Müller-Steinhagen 1. Klausur in "Technischer Thermodynamik I" 15.12.2009 (WS 2009/2010) ! Name:___________________ Fachr.:___________ Matr.-Nr.:______________ Es sind keine Hilfsmittel zugelassen. Zutreffende Aussagen sind anzukreuzen. Mehrere Antworten sind möglich. Falsche Antworten führen zu Punktabzug. Aufgabe 1 (9 Punkte) a) Eine reversible Zustandsänderung von 1-2 lässt sich im p,v-Diagramm wie folgt darstellen: Um welche Arbeit handelt es sich? Dissipationsarbeit Druckänderungsarbeit elektrische Arbeit mechanische Arbeit Volumenarbeit Oberflächenarbeit b) Eine reversible Zustandsänderung von 3-4 ist nachfolgend im p,v- und T,s-Diagramm dargestellt: Charakterisieren Sie die Zustandsänderung: - Welche Zustandsgröße bleibt konstant? Temperatur Druck Entropie Volumen - Wärme wird zugeführt wird abgeführt - Volumenarbeit muss zugeführt werden wird abgeführt tritt nicht auf. c) Welche der nachfolgenden Zusammenhänge gelten für ideale Gase? ·Ri =(-1)·cp cv =Ri /(-1) Ri =·cp/(-1) cv =Ri ·(-1) d) Bei der reversiblen adiabaten Kompression eines idealen Gases nimmt der Druck zu ab das Volumen zu ab die Temperatur zu ab. e) Ein ideales Gas wird isotherm (T=const.) in einem offenen System verdichtet. Die Zustandsänderung verläuft reversibel ohne Änderung des äußeren Systemzustandes. Markieren Sie die richtigen Aussagen: f) Es wird mehr Arbeit dem Gas zugeführt als Wärme abgeführt Es wird weniger Arbeit dem Gas zugeführt als Wärme abgeführt Die zugeführte Arbeit und die abgeführte Wärme sind gleich groß Die Änderung der Enthalpie des Gases ist ungleich Null Die Änderung der Enthalpie des Gases ist gleich Null Die Änderung der Enthalpie ist ungleich Null Die dem Gas zuzuführende Arbeit ist technische Arbeit Die dem Gas zuzuführende Arbeit ist Druckänderungsarbeit Die dem Gas zuzuführende Arbeit ist Volumenarbeit Die dem Gas zuzuführende Arbeit ist Verschiebearbeit Kennzeichnen Sie nachfolgend Formulierungen der thermischen Zustandsgleichung idealer Gase: U2 U1 m cv (T2 - T1 ) H2 H1 m cp (T2 - T1 ) p V n Ri T p v Ri T p V (m Rm T)/M p V (n Rm T)/M s2 - s1 cp ln(T2 / T1 ) - Ri ln(p2 / p1 ) s2 - s1 cV ln(T2 / T1 ) Ri ln(V2 / V1 ) g) Kennzeichnen Sie das T,s-Diagramm, in dem alle Zustandsänderung richtig eingezeichnet sind. h) Die spezifische Enthalpie eines idealen Gases ist nur eine Funktion vom Druck von der Masse von der Temperatur vom Umgebungszustand. i) Kennzeichnen Sie nachfolgend die Zustandsänderungen eines idealen Gases, bei denen eine Entropiezunahme auftritt: reversibel isotherme Entspannung reversibel isochore Druckabsenkung reversibel adiabate Entspannung. Formelzusammenstellung - 1. Hauptsatz: geschlossenes System U2 Ekin,2 Epot,2 U1 Ekin,1 Epot,1 Q12 W12 mit W12 WV,12 Wdiss,12 Wmech,12 dWv p dV h2 ekin,2 epot,2 h1 ekin,1 epot,1 m Q 12 P12 offenes System mit P12 m w t,12 , w t,12 w p,12 w diss,12 w mech,12 dwp v dp potentielle Energie epot g z , kinetische Energie ekin c2 /2 u2 u1 cV (T2 T1 ) , - ideale Gase: h2 h 1 cp (T2 T1 ) p T v T s2 s 1 cV ln 2 Ri ln 2 cp ln 2 Ri ln 2 T1 v1 T1 p1 p V m Ri T =cp/cv; Polytrope Zustandsänderung p v const. , n q12 cv bzw. p V m Ri T cp= cv + Ri T v n 1 const. , n κ T 2 T1 n 1 nn-1 T/ p const. - Umrechnung: 1 bar = 105 Pa = 105 N/m2= 105 J/m3 - Schwerebeschleunigung: g=9,81 m/s2 - Universelle (molare) Gaskonstante: Rm 8,314 J/(mol K), Rm M Ri , M m/n - Mathematische Zusammenhänge: du ln(u) u Es sind keine Hilfsmittel zugelassen. Bearbeitete Aufgaben werden als vollständig richtig bewertet, wenn neben dem korrekten Endergebnis auch der Rechengang ersichtlich ist. Aufgabe 2 (3 Punkte) In einer horizontal verlegten Rohrstrecke, in der Stickstoff (cp=1,0388 kJ/(kgK), Ri=0,2968 kJ/(kgK)) strömt, soll der Massenstrom mit Hilfe eines Durchflussmengenmessers ermittelt werden. In das Rohr ist ein elektrischer Widerstandsheizer, der eine elektrische Leistung von 500 W aufnimmt, eingebaut. Durch den vom Heizer verlustfrei an den Stickstoff abgegebenen Wärmestrom steigt die Stickstofftemperatur von 1=20°C um 3 K bei gleichbleibendem Druck von 1 bar. Es treten keine Wärmeverluste an die Umgebung sowie keine Änderungen von kinetischen Energien auf. Alle Stoffwerte können als konstant angenommen werden. a) Berechnen Sie den Massenstrom Stick stoff Berechnung: m =__________ kg/s b) Wie groß ist der Volumenstrom am Austritt aus der Rohrstrecke? Berechnung: V2 =__________ m3/s Aufgabe 3 (5 Punkte) In einer ruhenden Stahlflasche mit einem Volumen von V=50 l befindet sich Sauerstoff (ideales Gas; =1,395; cv=0,6577 kJ/(kgK)) bei einem Druck von p1=30 bar und einer Temperatur von 1=20°C. Die Gasflasche liegt in der Sonne, wodurch sich das Gas erwärmt und der Druck auf p2=36 bar ansteigt. Alle Stoffwerte können als konstant angenommen werden. a) Skizzieren Sie die als reversibel angenommene Zustandsänderung von 1 – 2 im nachfolgenden p,v- und T,s-Diagramm. Kennzeichnen Sie die Zustandspunkte 1 und 2. p T V b) Wie groß sind Arbeit und Wärme, die bei der reversiblen Zustandsänderung von 1-2 auftreten? Berechnung: Q12=__________ kJ W12=__________ kJ c) Skizzieren Sie jeweils die Wärme und die Arbeit in dem dafür geeigneten Diagramm der Teilaufgabe a) Aufgabe 4 (3 Punkte) Ein mit m=1 kg Luft (ideales Gas, cv=0,7179 kJ/(kgK); cp=1,005 kJ/(kgK)) gefüllter geschlossener Ballon (Anfangszustand 1: p1=1 bar, T1=300 K) wird mit einem konstanten Wärmestrom von 500 W beheizt. Die Zustandsänderung des Gases verlaufe reversibel polytrop mit n=-1,2. Alle Stoffwerte sind konstant. Nach 200 s Beheizungszeit platzt der Ballon. Wie groß sind Temperatur und Druck im Zustand 2, bei dem der Ballon platzt? T2=__________ K p2=__________ bar