physikalische chemie iii

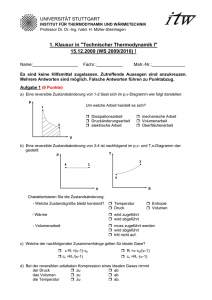
Physikalische Chemie I
Übungen zur Vorlesung PHYSIKALISCHE CHEMIE I
R. Strey / A. Müller / L.M. Feldmar / H. Klemmer
3. Übung
WS 2013/14
1. Irreversible, isotherme Zustandsänderung eines idealen Gases
Die Stoffmenge von drei Molen eines idealen Gases wird bei einer Temperatur von
27°C einer isothermen, irreversiblen Expansion gegen einen konstanten Druck von
1 bar unterworfen:
Expansion von einem Volumen VI = 20 dm3 auf ein Endvolumen von VII = 60 dm3.
Berechnen Sie:
a) die Arbeit W, die das System leistet;
b) die Wärmemenge Q, die das System aus dem Thermostaten aufnimmt;
c) die Änderung U der Inneren Energie des Systems;
d) die Änderung H der Enthalpie des Systems.
2. Reversible, isotherme Zustandsänderung eines idealen Gases
Die Stoffmenge von drei Molen eines idealen Gases wird bei einer Temperatur von
27°C einer isothermen, irreversiblen Zustandsänderung unterworfen:
Expansion von einem Volumen VI = 20 dm3 auf ein Endvolumen von VII = 60 dm3.
Berechnen Sie:
a) die Arbeit W, die das System leistet;
b) die Wärmemenge Q, die das System aus dem Thermostaten aufnimmt;
c) die Änderung U der Inneren Energie des Systems;
d) die Änderung H der Enthalpie des Systems.
3. Reversible, isotherme Zustandsänderung eines realen Gases
Die Stoffmenge von drei Molen Methan wird bei einer Temperatur von 27°C einer
isothermen, reversiblen Expansion unterworfen:
Expansion von einem Anfangsvolumen VI = 20 dm3 auf ein Endvolumen von
VII = 60 dm3.
Das Verhalten des Gases soll durch die VAN DER WAALS‘sche Zustandsgleichung mit
den Parametern
a = 2.28 dm6∙bar∙mol-2
b = 0.043 dm3∙mol-1
beschrieben werden.
Berechnen Sie:
a) die Arbeit W, die das System leistet;
b) die Wärmemenge Q, die das System aus dem Thermostaten aufnimmt;
c) die Änderung U der Inneren Energie des Systems;
d) die Änderung H der Enthalpie des Systems.
4. Reversible, adiabatische Zustandsänderung eines idealen Gases
Die Stoffmenge von drei Molen eines idealen zweiatomigen Gases wird bei der
Ausgangstemperatur von 300 K einer adiabatischen, reversiblen Zustandsänderung
unterworfen:
Expansion von einem Anfangsvolumen VI = 20 dm3 auf ein Endvolumen von
VII = 60 dm3. Das Verhältnis der Molwärme bei konstantem Druck und konstantem
Volumen habe den Wert cp/cv = 1.4.
Berechnen Sie:
a) die Temperaturänderung T;
b) die Arbeit W, die das System leistet;
c) die Änderung U der Inneren Energie des Systems;
d) die Änderung H der Enthalpie des Systems.
Vergleichen sie die Ergebnisse für die adiabatische Zustandsänderung mit den
Ergebnissen für die isotherme Zustandsänderung.
5. Enthalpieänderung
In einem Gefäß mit adiabatischen Wänden befindet sich bei einem Druck von 1 bar
und einer Temperatur von -10 °C die Masse m = 1 g unterkühltes Wasser. Es werden
Eiskeime erzeugt. Dadurch bildet sich spontan ein heterogenes System, in dem Eis
und Wasser bei einer Temperatur von 0 °C koexistieren.
Berechnen Sie die Massen mW und mE des Wassers und des Eises, die im
Gleichgewicht vorliegen, aus folgenden Daten:
spezifische Wärme des Wassers
cp(W) = 4.18 J/(g∙K)
spezifische Wärme des Eises
cp(E) = 2.09 J/(g∙K)
Schmelzenthalpie des Eises bei 0 °C SH0 = 311 J/g
Die spezifischen Wärmen können im betrachteten Temperaturbereich als konstant
angenommen werden.