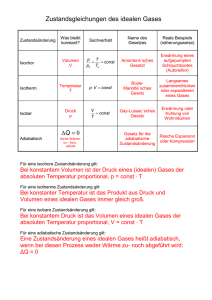
ν 9/8 ν 5/4 ν 4/3 ν 3/2 ν 5/3 ν 15/8 ν 2/1 ν

• Diese sind in Oktaven gegliedert, wobei sich die Frequenzen des tiefsten
und höchsten Tons einer Oktave um den Faktor zwei unterscheiden.
• Innerhalb der Oktave unterteilt man die Töne in 12 Halbtonschritte,
die bei der temperierten Stimmung ein festes Frequenzverhältnis von
√
12
2 zueinander aufweisen.
• In der Dur-Tonleiter werden diejenigen dieser Halbtöne verwendet, die
entstehen, die zur Grundfrequenz annähernd im Verhältnis 9:8, 5:4,4:3,3:2,5:3
und 15:8 stehen (Sekunde, Terz, Quart, Quint, Sext, Septime, die exakten Verhältnisse entsprechen der reinen Stimmung).
ν0
9/8 ν0
5/4 ν0
4/3 ν0
3/2 ν0
5/3 ν0
15/8 ν0
2/1 ν0
3.2.16
Schallerzeugung und -aufnahme beim Menschen
• Die Schallerzeugung im Kehlkopf geschieht im Prinzip wie bei den Musikinstrumenten durch Anregung von stehenden Wellen auf den Stimm81
bändern. Da diese bei Männern länger sind als bei Frauen, haben erstere tiefere Stimmen. Die eigentliche Klangfärbung und Lautbildung
wird durch Ausbildung stehender Wellen in den zahlreichen Lufträumen nach dem Kehlkopf (Rachen-, Mund- und Nasenraum) erreicht.
• Die Schallwahrnehmung ist deutlich komplizierter. Zunächst wird der
Schall durch ein gekoppeltes Membransystem von der Luft in die flüssige Perilymphe übertragen. Die Auflösung in verschiedene Frequenzen,
also im Prinzip die Fourier-Analyse, wird in der Ohrschnecke vorgenommen. Dort befinden sich in der Basilarmembran Resonatoren (Querfasern) mit unterschiedlichen Resonanzfrequenzen an unterschiedlichen
Orten (hohe Frequenzen am Eingang, niedere am Ende der Schnecke).
82
83
84
4
Wärmelehre
Wir werden uns hier auf die fundamentalen Aussagen der Wärmelehre beschränken, da die Wärmelehre auch Gegenstand der Chemie ist. Die Aussagen
der Wärmelehre sind von ausserordentlicher Wichtigkeit für unser gesamtes
Weltbild und in ihrer Fundamentalität von kaum einem anderen Bereich der
Physik erreicht. Die Wärmelehre trifft Aussagen über das mittlere Verhalten
von Vielteilchensystemen
85
4.1
Das ideale Gas
• Unter einem idealen Gas verstehen wir eine grosse Anzahl von Massenpunkten (also Teilchen ohne Volumen), die ausser elastischen Stössen
keine Wechselwirkung miteinander eingehen.
4.1.1
Zustandsgrössen des idealen Gases
• Wenn wir den Zustand eines idealen Gases beschreiben wollen, könnten
wir nach den Gesetzen der Mechanik die Trajektorien aller Teilchen
beschreiben. Das ist jedoch bei der ungeheuren Anzahl von Teilchen
unmöglich. Also müssen wir versuchen, Grössen zu finden, die zur Beschreibung des Gases besser geeignet sind.
• Um eine bestimmte Menge eines idealen Gases betrachten zu können,
müssen wir es zunächst von seiner Umgebung abgrenzen. Dazu wird eine Kraft notwendig sein. Diese Kraft auf die Oberfläche der Gasmenge
bezogen ergibt einen Druck p, den andererseits das Gas auf die Begrenzung ausübt. Die Begrenzung grenzt ein Volumen V ein, in dem
sich eine bestimmte Zahl von Teilchen befindet. Die Zahl der Teilchen
können wir über die Avogadro-Konstante NA und die Stoffmenge n ausdrücken: N = nNA . Weiterhin werden die Teilchen des idealen Gases
eine kinetische Energie haben. Diese ist jedoch sehr schwer direkt zu
messen. Wir führen deshalb als neue Zustandsgrösse die Temperatur T
ein, die, wie wir sehen werden, direkt mit der kinetischen Energie der
Teilchen verknüpft ist. Die Einheit der Temperatur ist das Kelvin (K).
• William Thomson, seit 1866 Sir William Thomson, seit 1892 1. Baron
Kelvin of Largs, meist als Lord Kelvin bezeichnet, (* 26. Juni 1824
in Belfast, Nordirland; † 17. Dezember 1907 in Netherhall bei Largs,
Schottland)
Andere Temperaturskalen
86
• Neben der Kelvin-Temperaturskale existieren noch andere Temperaturskalen, z.B. die Celsius-Skala. Sie ist so festgelegt, dass unter Normalbedingungen (wir werden noch sehen, wie diese aussehen) der Eispunkt des Wassers bei 0C und der Siedepunkt des Wassers bei 100C
liegt, sie ergibt sich aus der Kelvin-Skala durch Abzug von 273.15°C.
• Wie wir sehen werden, reichen Temperatur, Druck, und Volumen aus,
um den Zustand eines idealen Gases zu beschreiben.
4.1.2
Zustandsänderungen
Experimentell wurden folgende Zusammenhänge zwischen den Zustandsgrössen bei geschlossenen Behältern gefunden:
• Bei konstanter Temperatur ist der Druck dem Volumen indirekt proportional: p ∝ V1 . Eine solche Zustandsänderung nennen wir isotherme
Zustandsänderung. In einem p − V -Diagramm erhalten wir für die isotherme Zustandsänderung eine Hyperbel:
• Bei konstantem Druck ist das Volumen proportional zur Temperatur: V ∝ T . Das ist das 1. Gay-Lussacsche Gesetz. Eine solche Zustandsänderung nennen wir isobare Zustandsänderung. In einem V −T Diagramm erhalten wir eine Gerade. Flüssigkeiten zeigen ein ähnliches
Verhalten bei Temperaturänderung. Da Flüssigkeiten zusätzlich inkompressibel sind, kann man die Volumenänderung zur Temperaturmessung verwenden.
• Bei konstantem Volumen ist der Druck proportional zur Temperatur:
p ∝ T . Das ist das 2. Gay-Lussacsche Gesetz. Eine solche Zustandsänderung nennen wir isochore Zustandsänderung. In einem p − T Diagramm erhalten wir eine Gerade. Die Proportionalität von Druck
und Temperatur kann man nutzen, um die Temperatur zu messen: Eine
solche Vorrichtung heisst Gasthermometer.
87
h
pGas=ρgh
• Die mechanische Arbeit, die bei einer Zustandsänderung verrichtet wir,
kann man sich verdeutlichen, wenn man ein Gas in einem Zylinder
betrachtet, in dem man einen Kolben bewegen kann. Die Kraft auf den
Kolben berechnet sich nach FN = Ap.
• Damit erhalten wir für die Arbeit dW = F dx = Apdx = pdV . Anschaulich ist dies die Fläche unter der Kurve in einem p–V–Diagramm.
4.1.3
Kinetische Gastheorie
• Die kinetische Gastheorie stellt einen Zusammenhang zwischen der mikroskopischen Bewegung der Teilchen und den statistischen Grössen
der Thermodynamik her.
88
• Dabei wird der Impulsübertrag der Teilchen, die in einem bestimmten
Zeitintervall auf die Gefässwand treffen, betrachtet.
• Jedes Teilchen überträgt jetzt beim (elastischen) Stoss auf die Wand
den Impuls
∆px = 2px
Die Zahl der je Zeiteinheit auf die Wand treffenden Teilchen ist
n
% |px |
∆n
= Ax vx = Ax
∆t
V
2
m
wobei der Faktor 12 der Tatsache Rechnung trägt, dass gleich viele Teilchen positives und negatives Vorzeichen des Impulses haben.
• Insgesamt haben wir einen Impulsübertrag auf die Wand von
p2
∆n
∆px = %Ax x
∆t
m
Dieser Impulsübertrag je Zeit entspricht der Normalkraft auf die Wand,
p2x
p2x
Fn
so dass wir für den Druck erhalten: p = A
=
%
⇒
pV
=
n
.
m
m
x
• Die Zahl der Teilchen lässt sich durch die Stoffmenge, multipliziert mit
der Avogadro-Zahl, ausdrücken. Damit haben wir einen Zusammenhang
zwischen den makroskopischen Grössen Druck und Volumen und dem
mikroskopischen Impuls gefunden.
• Bisher haben wir noch nicht die unterschiedlichen Geschwindigkeiten
der Teilchen betrachtet (wir erinnern uns, dass beim elastischen Stoss
die Geschwindigkeiten vor und nach dem Stoss verschieden sein können). Was wir suchen, ist der statistische Mittelwert des Impulses, um
auch auf der rechten seite makroskopische Grössen zu finden. Die Verteilung der Geschwindigkeiten gehorcht der Maxwellschen Geschwindigkeitsverteilung:
•
4n m 3/2
mv 2
dn(v) = √
exp −
dv
2kT
π 2kT
89
• Hierbei ist k die Boltzmann-Konstante mit dem Wert k = 1, 38066 ·
10−23 JK−1 .
• James Clerk Maxwell (eigentlich James Clerk; * 13. Juni 1831 in Edinburgh; † 5. November 1879 in Cambridge) war ein schottischer Physiker. Er war der letzte Repräsentant der jüngeren Linie der bekannten
schottischen Familie Clerk of Penicuik.
• Ludwig Boltzmann (* 20. Februar 1844 in Linz; † 5. September 1906
in Duino bei Triest) war ein österreichischer Physiker und Philosoph
• Mittelt man diese Geschwindigkeitsverteilung, so findet man:
1 2 3
m v = kT
2
2
• Das ist aber gerade die mittlere kinetische Energie. Wir sehen also, dass
die mittlere kinetische Energie über die Boltzmann-Konstante mit der
Temperatur verknüpft ist.
• Da wir bisher Massenpunkte betrachtet haben, können diese nur kinetische Energie der Translation besitzen.
• Erweitern wir die Betrachtung auf Teilchen, die aus mehreren Massenpunkten zusammengesetzt sind, so können diese auch kinetische Energie der Rotation besitzen. Insgesamt gilt der Gleichverteilungssatz:
• Alle Freiheitsgrade der Bewegung (Translation und Rotation) sind gleichberechtigt, und der Zusammenhang zwischen Temperatur und kinetischer Energie dieses Freiheitsgrades ist gegeben durch
1
< Ekin >= kT
2
90
•
2
• Setzt man diesen Mittelwert in pV = n pm ein, so gelangt man zur
Zustandsgleichung des idealen Gases:
• pV = nRT .
• Hier ist n die Stoffmenge und R die allgemeine Gaskonstante mit dem
Zahlenwert R = 8, 31 Jmol−1 K−1 , die sich aus der Boltzmann-Konstante
multipliziert mit Avogadro-Zahl zusammensetzt: R = NA k.
• (Lorenzo Romano) Amedeo (Carlo) Avogadro (kurz Amedeo Avogadro), Conte de Auaregna e Ceretto (* 9. August 1776 in Turin; † 9. Juli
1856 in Turin) war ein italienischer Physiker und Chemiker.
• Betrachten wir ein mol eines Gases und setzen wir für die Temperatur den sogenannten Normalwert von 273,15 K und für den Druck von
101325 Pa ein, so erhalten wir das molare Volumen des idealen Gases
Vm = 22, 4 lmol−1 . Allgemein können sich natürlich alle Zustandsgrössen bei einem bestimmten Prozess ändern, man kann jedoch jede beliebige Zustandsänderung in infenitesimal kleine isobare, isochore oder
isotherme Prozesse zerlegen.
91
4.1.4
Gasgemische
• Da die Teilchen eines idealen Gases nicht wechselwirken, werden auch
die Teilchen eines Gemisches von Gasen nicht wechselwirken.
• Bei einer Mischung von Gasen in einem Gefäss wird sich jedes so ausbreiten, als wäre das andere nicht vorhanden.
• Für jede Komponente der Mischung wird also die Zustandsgleichung
gelten: pi V = ni RT .
• Hier haben wir implizit schon einen Hauptsatz der Thermodynamik angenommen, nämlich, dass in einem solchen Gemisch alle Komponenten
die gleiche Temperatur haben.
• Der Gesamtdruck p wird sich jetzt aus der Summe der Drücke der
P
Komponenten, der Partialdrücke pi , ergeben: p =
pi . Dies nennt
man das Daltonsche Gesetz.
4.2
Reale Gase
• In einem realen Gas kann man das Eigenvolumen der Teilchen und die
Kräfte zwischen diesen nicht mehr vernachlässigen.
• Das zur Bewegung zur Verfügug stehende Volumen wird also durch das
Eigenvolumen vermindert.
• Gleichzeitig führt die gegenseitige Anziehung der Teilchen (wir erinnern
uns an die Oberflächenspannung) zu einem zusätzlichen Druck, dem
Binnendruck.
• Beidem trägt die Van der Waals–Zustandsgleichung Rechnung: (p +
a
)(V − b) = nRT .
V2
• Die Graphische Auftragung einer Van der Waals–Isotherme im p–V–
Diagramm zeigt Bereiche, in denen mit steigendem Volumen der Druck
steigt.
92
• Ein solcher Zustand ist physikalisch nicht sinnvoll.
• Experimentell beobachtet man eine Änderung des Volumens ohne eine
Druckänderung sowie die Koexistenz zweier Phasen, einer flüssigen und
einer gasförmigen. Wir werden auf Phasenübergänge später nochmals
zurückkommen.
• Die Isobare des Phasenübergangs im p–V–Diagramm wird so festgelegt,
dass die Flächen zwischen isobare und Van der Waals–Isotherme sich
gerade aufheben.
4.3
4.3.1
Hauptsätze der Thermodynamik
Wärme und Temperatur
• Wir hatten bereits in der Mechanik eine Art der Arbeit kennengelernt,
die wir in eine nicht mechanische Energieform verwandelten: Die Reibungsarbeit.
• Sie führte nicht zur Erhöhung der kinetschen oder potentiellen Energie.
93
• Nach dem Energieerhaltungssatz kann Energie jedoch nicht verloren
gehen, sie muss also in das System (Klotz auf Tisch) gesteckt worden
sein.
• Unsere Erfahrung lehrt uns, dass Reibung dazu führt, dass sich die
Temperatur des Körpers erhöht. Ausserdem lehrt uns die Erfahrung,
dass zwei Körper, die unterschiedliche Temperatur haben, den Temperaturunterschied ausgleichen, wenn wir sie in Kontakt bringen.
• Diese Erfahrung wird manchmal als Nullter Hauptsatz der Wärmelehre bezeichnet.
• Wir hatten eben gesehen, dass die mittlere kinetische Energie der Teilchen mit der Temperatur in einem direkten Zusammenhang steht. Es
muss also eine Energieform zwischen den beiden Körpern übertragen
worden sein. Diese Energieform nennen wir Wärme. Die Wärme ist also
stets an einen Prozess gekoppelt, sie ist eine Prozessgrösse
4.3.2
Temperatur und Wärmekapazität
• Wie können wir jetzt messen, wieviel Wärme einem Körper zugeführt
wurde?
• Wir hatten gesehen, dass es einen direkten Zusammenhang zwischen
der kinetischen Energie der Teilchen und der Temperatur gab.
• Zur Messung der Temperatur kann man eine grosse Anzahl von Effekten
nutzen, die eine Temperaturabhängigkeit zeigen. Wir werden gegebenenfalls bei solchen Effekten auf die Temperaturmessung zurückkommen. Das Gasthermometer als Beispiel haben wir bereits kennengelernt.
• Experimentell wird eine Proportionalität zwischen zugeführter Wärme
und Temperatur gefunden: ∆T ∝ δQ.
• Wir schreiben hier ein kleines Delta, da es sich nicht um eine “echte”
Differenz handelt, sondern eben um eine übertragene Wärmemenge.
94
• Die Proportionalitätskonstante heisst Wärmekapazität C :=
der Einheit JK−1 .
δQ
∆T
mit
• Beziehen wir die Wärmekapazität auf die Masse des Körpers, so erC
halten wir die spezifische Wärmekapazität c = m
mit der Einheit
−1
−1
JK kg .
4.3.3
Die innere Energie
• Wenn wir einem Körper Wärme zuführen, so führen wir dem Körper
Energie zu.
• Diese muss jetzt also “in dem Körper stecken”. Wir nennen diese in dem
Körper enthaltene Energie innere Energie U .
• Sie ist bei einem idealen Gas gleich der Summe der mittleren kinetischen
Energien der Teilchen: U = n < Ekin >= n f2 kT , wobei f die Zahl der
Freiheitsgrade ist.
• Die innere Energie ist eine Zustandsfunktion, das heisst, Änderungen
der inneren Energie zwischen zwei Zuständen sind unabhängig vom
Weg.
4.3.4
Der erste Hauptsatz der Thermodynamik
• Der erste Hauptastz der Thermodynamik erweitert das aus der Mechanik bekannte Prinzip der Energieerhaltung um die Wärmeenergie.
• Er besagt, dass die Änderung der inneren Energie gleich der Summe
aus zugeführter Wärme und am System verrichteter Arbeit ist:
dU = δQ + δW
Man kann auch sagen, dass keine Maschine existert, die ohne Energiezufuhr permanent Arbeit verrichtet (Perpetuum Mobile 1. Art).
95
• Auch die Arbeit ist eine prozessabhängige Grösse (im Gegensatz zur
zustandsabhängigen inneren Energie), deshalb auch hier das δ.
• Mit der Inneren Energie können wir jetzt die Wärmekapazität von Gasen angeben, wobei wir sehen werden, dass es zwei verschiedene Wärmekapazitäten gibt.
• Halten wir zunächst das Volumen des Gases konstant, so ist die zugeführte Wärme gleich der Änderung der inneren Energie.
• Mit dU = f2 RdT erhalten wir für die Wärmekapazität bei konstantem
Volumen
dU
f
δQV
=
= R
cV =
dT
dT
2
.
• Um die Wärmekapazität bei konstantem Druck zu erhalten, setzen wir
im ersten Hauptsatz für die Arbeit −pdV ein. Bei konstantem Druck
erhalten wir aus der Zustandsgleichung des idealen Gases V = RT
:
p
dV =
R
dT
p
. Damit wird der erste Hauptsatz zu
δQ = dU − δW =
f
f
RdT + pdV = RdT + RdT
2
2
. Damit erhalten wir für die Wärmekapazität bei konstantem Druck:
cp =
δQ
f
= R( + 1)
dT
2
• Weiterhin sehen wir, dass gilt:
cp − cV = R
• Die Wärmekapazität bei konstantem Druck ist also grösser als die bei
konstantem Volumen. Das ist auch einsichtig, da ein Teil der zugeführ96
ten Wärme nicht zu einer Erhöhung der inneren Energie und damit zur
Temperaturerhöhung beiträgt, nämlich der Teil, der als Volumenarbeit
vom System verrichtet wird.
• Wir hatten bereits verschiedene Zustandsänderungen eines idealen Gases kennengelernt: Die isotherme, isobare und isochore Zustandsänderung.
• Bei der isothermen gilt dU = 0, bei der isochoren δW = 0.
• Jetzt können wir im ersten Hauptsatz noch δQ = 0 setzen. Eine solche
Zustandsänderung heisst adiabatisch. Wir erhalten:
f
RT
RdT = −pdV = −
dV
2
V
• Das ist wieder eine Differentialgleichung, wobei wir hier eine Trennung
= − dV
, das heisst, auf jeder
der Variablen vornehmen können: f2 dT
T
V
Seite stehen jetzt nur noch Funktionen und Ableitungen einer Grösse.
• Hier können wir integrieren und erhalten: f2 ln TT0 = − ln VV0 und unter
f
Anwendung der Logarithmen-Gesetze: ln( TTo ) 2 = ln( VV0 )−1 .
• Delogarithmieren führt schliesslich zu
V
T
= ( )−γ
T0
V0
oder T V γ = konst mit γ = f2 .
• Setzen wir dies in die Zustandsgleichung des idealen Gases ein, so erhalten wir pV κ = konst oder ( pp0 ) = ( VV0 )−κ mit κ = f +2
.
f
• Im Vergleich zur Isothermen ( pp0 ) = ( VV0 )−1 verläuft eine Adiabate im
p–V–Diagramm also steiler. Das muss auch so sein, da ja bei einer
adiabatischen Zustandsänderung bei gleicher verrichteter Arbeit keine
Wärme abgegeben wird, also die gesamte Arbeit in einer Änderung der
inneren Energie (Temperaturänderung!) resultiert .
97
• Hier nochmal alle Prozesse graphisch dargestellt:
98
4.3.5
Reversible und irreversible Prozesse
• Nach dem ersten Hauptsatz sind alle Energieformen gleichberechtigt
und damit beliebig ineinander umwandelbar.
• Das heisst, wenn wir einen Klotz betrachten, dem wir eine Anfangsgeschwindigkeit gegeben haben, so wird die Reibungsarbeit zu einer
Erhöhung der inneren Energie des Systems Klotz–Tisch führen.
• Nach dem ersten Hauptsatz könnte jedoch auch der umgekehrte Prozess
ablaufen: Innere Energie des Systems Klotz–Tisch wird dazu verwendet,
Beschleunigungsarbeit zu verrichten.
• Ein solcher Prozess wird aber nicht beobachtet. Offensichtlich gibt es
Prozesse, die nicht umkehrbar (irreversibel) sind.
• Das ist eigentlich ziemlich erstaunlich. Nach den Newtonschen Axiomen
dürfte es so etwas nicht geben, zumindest, wenn man nur konservative
Kräfte zulässt. Nun sind die fundamentalen Wechselwirkungen in der
Natur aber alle konservativ. Dennoch gibt es nach unserer Erfahrung
irreversible Prozesse. Reversible Prozesse sind zum Beispiel die adiabatische oder die isotherme Zustandsänderung eines idealen Gases.
99
4.3.6
Entropie
• Für die Arbeit δW hatten wir für eine reversible Zustandsänderung
beim idealen Gas gefunden: δWrev = −pdV .
• Gibt es einen analogen Ausdruck für δQrev ? Das heisst, gibt es eine
Zustandsgrösse analog zu dV ?
• Wir können eine solche definieren: dS := dQTrev . Dies ist die Definition
der Entropie S, die eine Zustandsgrösse wie Temperatur, Druck und
Volumen ist.
• Da sie nur vom Zustand abhängig ist, muss eine Änderung unabhängig
vom Weg sein.
• Betrachten wir jetzt das System und seine Umgebung, so entspricht
bei reversibler Prozessführung die Entropieänderung des Systems genau
der negativen Entropieänderung der Umgebung.
• Ein Beispiel wäre die isotherme Expansion eines Gases gegen den Druck
p auf das doppelte Volumen.
• Denselben Prozess können wir im Prinzip irreversibel durchführen: Wir
betrachten einen Behälter, der in zwei Hälften getrennt ist, wobei sich
in der einen Hälfte ein Gas unter dem Druck p befindet. Entfernen
wir jetzt die Trennwand, so wird sich das Gas im gesamten Behälter
ausbreiten.
• Die Entropieänderung des Systems ist die gleiche wie bei der isotherme Expansion, jedoch haben wir jetzt keine Entropieänderung in der
Umgebung.
• Damit hat sich die Gesamtentropie von System und Umgebung erhöht,
man spricht von einem irreversiblen Prozess.
• Betrachten wir System und Umgebung als neues Gesamtsystem, so
sprechen wir von einem abgeschlossenen System. Ein abgschlossenes
100