Physikalische Chemie WiSe 2013/14 Dozent: Prof. Dr. Michael

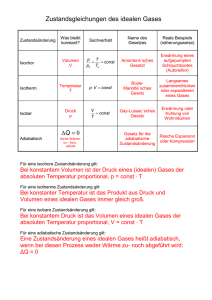
Physikalische Chemie WiSe 2013/14 Dozent: Prof. Dr. Michael Winklhofer, http://www.geophysik.uni-­‐muenchen.de/Members/michael Kontakt: [email protected]­‐muenchen.de oder [email protected] Sprechzeiten: nach der VL Organisatorisches: -­‐
Keine Veranstaltung am 23.10 sowie in den Herbstferien (27.10 und 30.10) -­‐
Modus: 4 SWS (Mo 16-­‐18 Uhr und Mi 12-­‐14 Uhr, jeweils B52) Erstsemestler können ab Mitte Dezember aufhören -­‐
1. Klausur: Mitte Dezember -­‐
2. Klausur: Februar – NUR FüR HöHERE SEMESTER (3.+5.) -­‐ Übungen sind auf freiwilliger Basis, sollten aber als Vorbereitung für die Klausur 1 Klausur fuer 1.Semester, 2 Klausur fuer 3./5. Literatur: Czeslik, C., H. Seemann und R. Winter (2010) Basiswissen Physikalische Chemie, 4. Auflage, Vieweg+Teubner, Wiesbaden. Atkins, P. W. und J. de Paula (2006) Physikalische Chemie, 4. Auflage, Wiley-­‐VCH. Übersicht über Inhalte: A) Thermodynamik (alle Teilnehmer, bis Mitte Dezember). Gasgesetze (ideales Gas); Zustandsänderungen, therm. Gleichgewicht, Wärmekapazität, Innere Energie, Enthalpie, Entropie Energieerhaltungssatz (1. Hauptsatz) reales Gas Phasenübergänge, allgemein Thermodynamik chemischer Reaktionen; Redox-­‐ und Elektrochemie B) Spektroskopie (für höhere Semester) Molekulare Spektroskopie: Rotations-­‐ und Vibrationsspektren Atomare Spektroskopie: Charakteristische Röntgenstrahlung A) THERMODYNAMIK: 1) Ideales Gas: Definit Ideales Gasgesetz: pV = n RT (1a) oder pV = N kB T (1b) p: vom Gas ausgeübter Druck [ in Pa = N/m2 ] V: vom Gas eingenommenes Volumen, in m3 = 106 cm3 T: absolute Temperatur des Gases in K (T/K = 𝜗/℃ – 273.15) n: Stoffmenge des Gases in Mol; 1 Mol enthält NA = 6.022 ∙ 10!" Teilchen R: Allgemeine Gaskonstante, R=8,3145 J/K/mol = NA kB N= n NA: Anzahl der Gasteilchen im Volumen kB : Boltzmann-­‐Konstante, kB =1.38 ∙ 10!!" J/K Standardbedingungen: TS=298.15 K (𝜗 = 25℃) sowie pS = 1 bar = 105 Pa. Wichtige praktische Anwendungen von (1): -­‐ Erlaubt Molmassen-­‐Bestimmung: pV = (m/M) RT n = m/M (m = Gesamtmasse des Gases, M=dessen molare Masse) ρ=m/V => M= ρ RT/p -­‐ Temperaturmessung mit Gasthermometer -­‐ Historisch: Bestimmung des Absoluten Nullpunktes der Temperatur durch Extrapolation der p(T) Geraden nach p=0. Daltonsches Gesetz der Partialdrücke (=> Übungsaufgabe) !"#$!! !"# !"#$%#&"!"
𝑝!"! = !!!
𝑝! mit 𝑝! = 𝑛! 𝑅𝑇/𝑉 Innere Energie (proportional zur Temperatur). Am Beispiel des Idealen Gases lassen sich mikroskopische kinematische Groessen mit thermischen Eigenschaften vernkuepfen: !
Ekin/atom = 𝜇 𝑣 ! !
𝜇 ist die Masse eines Gasatoms 𝑣 sei die typische Geschwindigkeit der Gasatome bei gegebener Temperatur: Maxwell-­‐Boltzmann: !"
< 𝑣 ! > = 3 (quadratische gemittelte Geschwindigkeit) !
!
! !
! ! !"
!
< 𝑣 ! > =
= 𝑘! T Ekin/atom = 𝜇 𝑣 ! =
!
!! !
!! ! !
!
Gesamte kinetische Energie aller N Atome im Gas bei Temperatur T !
!
𝐸!"# = 𝑁 𝑘! T = 𝑛𝑅T !
!
Faktor 3: 3 Freiheitsgrade der Translation (< 𝑣!! >=< 𝑣!! >=< 𝑣!! >=< 𝑣 ! >/2 !
Innere Energie: 𝑈 = 𝑛𝑅T !
Erhöhung der inneren Energie durch Temperaturerhöhung um ΔT: !
bei konstanten Volumen (isochor): Δ𝑈 = 𝑛𝑅 ΔT !
!
!!
Allgemein: lim!!→!" = 𝐶! ideales Gas: 𝐶! = 𝑛𝑅 !
!!
Isotherme Prozess ändern die Innere Energie des Gases nicht! Es muss Arbeit am Gas geleistet werden oder vom Gas verrichtet werden. Isotherme Zustandsänderung : pV = const <= T = const => U=const Bsp: Isotherme Expansions eines Gases (im “Wasserbad”, einem Wärmereservoir) gegen den äußeren Druck pa. (z.B. oberer Ast des Carnot-­‐Prozesses) Welche Arbeit leistet das Gas? Expansion (Volumenzunahme) ΔV = V2 − V1>0 Druck-­‐Arbeit: dW = -­‐F (z) dz = -­‐ p(V) dV !!
!!
1
W = −
𝑝 𝑉 𝑑𝑉 = −𝑛𝑅𝑇
𝑑𝑉 = − 𝑛𝑅𝑇 𝑙𝑛𝑉2 − 𝑙𝑛𝑉1 !!
!! 𝑉
𝑉2
W = −𝑛𝑅𝑇𝑙𝑛
𝑉1
Da das System Arbeit leistet, müßte es seine innere Energie verringern, also abkühlen. Dies passiert aber nicht, weil der Prozess ja isotherm ablaufen soll. Folglich nimmt das Gas Wärmemenge Q aus dem Reservoir, um damit Arbeit zu verrichten. 1. Hauptsatz: ΔU = ΔQ + ΔW ; hier ΔU =0 => ΔQ = -­‐Δ W => ΔQ > 0 wenn das System arbeit leistet Dabei wird die Entropiemenge ΔS= ΔQ/T an das Gas gegeben. ( später: 1. Hauptsatz: ΔU = T ΔS -­‐ 𝑝ΔV ;) Jetzt: Betrachte Kompression des Gases auf der unteren Isotherme T2 < T1: Hier muss Arbeit am System verrichtet werden, welches nun Wärme an das (kältere Reservoir) abgibt. Gas nimmt beim oberen isothermen Prozess die Entropiemenge ΔS1= +ΔQ1/T1 auf und gibt ΔS2 = -­‐ΔQ2/T2 ab. Also ist Zufluss und Abfluss von Entropie gleich. Der Zweite Hauptsatz besagt nun, dass sich die Gesamtentropie (System + Umwelt) trotzdem erhöht. Der Wirkungsgrad ist deshalb höchstens: 1 – T2/T1 Adiabatische Zustandsänderung : ΔQ =0 => ΔU = -­‐ 𝑝ΔV ;) (schnelle Prozess ohne Wärmeaustausch mit der Umgebung: ) ΔU = -­‐ 𝑝ΔV bzw. mit der Definition oben, C! ΔT = -­‐ 𝑝ΔV Übergang zu infinitesimalen Änderungn: dT, dV => C! dT = −𝑝𝑑𝑉 !"#
Einsetzen der Gasgleichung: C! dT = −
𝑑𝑉 !
Differentialgleichung, die durch Variablenseparation gelöst werden kann: dT
𝑛𝑅𝑇 𝑑𝑉
=−
𝑇
C! 𝑉
jetzt wieder von (p1,V1) nach (p2,V2): !!
dT
𝑛𝑅 !! 𝑑𝑉
=−
C! !! 𝑉
!! 𝑇
𝑇2 𝑛𝑅 𝑉1
ln
=
ln 𝑇1 C! 𝑉2
da exp(a ln(x))=xa also: 𝑉1
𝑇2
=
𝑇1
𝑉2
𝑇𝑉
!"
!!
!"
!!
= 𝑐𝑜𝑛𝑠𝑡 𝑇𝑉 ! = 𝑐𝑜𝑛𝑠𝑡 und 𝑝𝑉 !!! = 𝑐𝑜𝑛𝑠𝑡 !
mit 𝐶! = 𝑛𝑅 haben wir a=2/3 !
Beispiel: Berechnen Sie den Temperaturabfall bei adiabatischer Expansion auf das zehnfache das ursprünglichen Volumens.