Kieferorthopädische Biomechanik

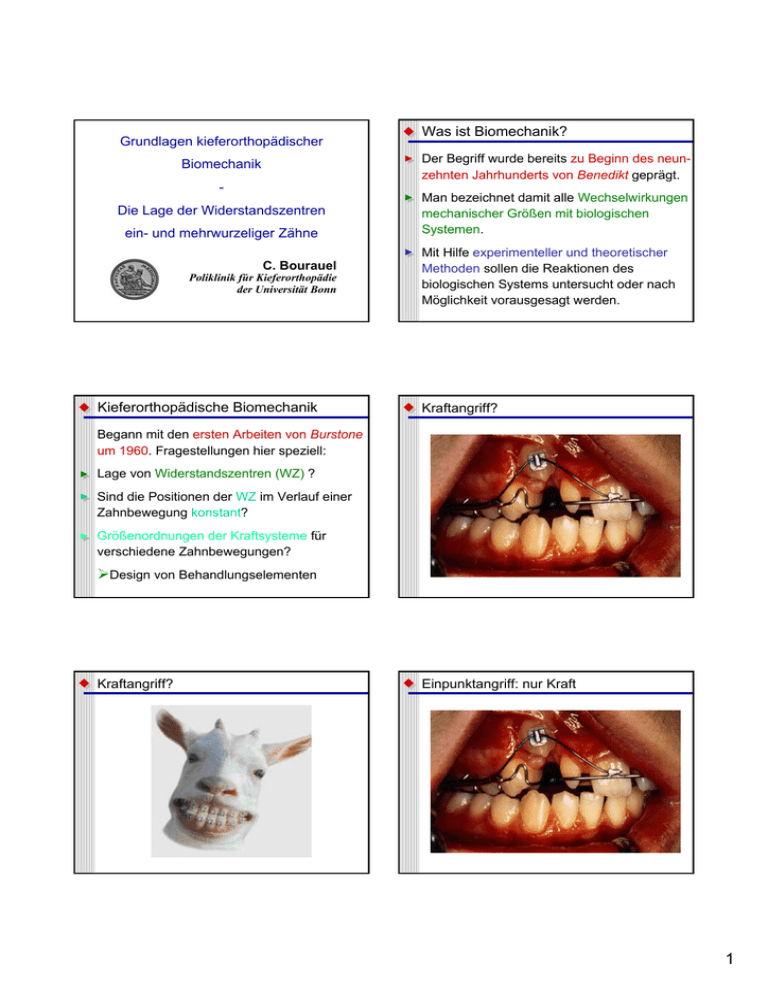
Grundlagen kieferorthopädischer
Was ist Biomechanik?
Der Begriff wurde bereits zu Beginn des neunzehnten Jahrhunderts von Benedikt geprägt.
Biomechanik
Die Lage der Widerstandszentren
ein- und mehrwurzeliger Zähne
C. Bourauel
Poliklinik für Kieferorthopädie
der Universität Bonn
Kieferorthopädische Biomechanik
Man bezeichnet damit alle Wechselwirkungen
mechanischer Größen mit biologischen
Systemen.
Mit Hilfe experimenteller und theoretischer
Methoden sollen die Reaktionen des
biologischen Systems untersucht oder nach
Möglichkeit vorausgesagt werden.
Kraftangriff?
Begann mit den ersten Arbeiten von Burstone
um 1960. Fragestellungen hier speziell:
Lage von Widerstandszentren (WZ) ?
Sind die Positionen der WZ im Verlauf einer
Zahnbewegung konstant?
Größenordnungen der Kraftsysteme für
verschiedene Zahnbewegungen?
¾Design von Behandlungselementen
Kraftangriff?
Einpunktangriff: nur Kraft
1
Übersicht 1 (Allgemeiner Teil)
Kraft- und Drehmomentschlüssiger Angriff
Mechanische / physikalische Grundbegriffe
•
•
•
Koordinatensysteme und Vektoren
Kräfte und Drehmomente, Kraftsysteme
Einheitensystem
Die Wirkung von Kraftsystemen auf Körper
•
•
•
•
•
•
Starrer Körper
Schwerpunkt des starren Körpers
Translationen und Rotationen
Übersicht 2 (Allgemeiner Teil)
Übersicht 3 (Spezieller Teil)
Der Zahn als starrer Körper
Aktuelle Probleme orthodontischer Biomechanik
Parodontale Lagerung und Widerstandszentrum
• Kieferorthopädische Grundlagen (Wdh.):
WZ, RZ, M/F-Verhältnis
Wechselwirkungen des Zahns mit Kraftsystemen
• Materialeigenschaften des Zahnhalteapparats
Rotationszentrum
• Lage des Widerstandszentrums einwurzeliger Zähne
mehrwurzeliger Zähne
Bewegungsarten und Drehmoment/Kraft-Verhältnis
•
•
eines Frontzahnblocks
appliziertes, äquivalentes und effektives Kraftsystem
• Mathematisches Modell der Zahnbewegung
M/F:
• Verifizierung an Hand klinischer Beispiele
Das Drehmoment / Kraft-Verhältnis
Kieferorthopädische Kraftsysteme und Arten der
Zahnbewegung
Mechanische / physikalische Grundbegriffe
Die Mechanik ist ein Teilgebiet der Physik. Die
Biomechanik wiederum ist ein Spezialgebiet,
das mit physikalischen Methoden das
Verhalten biologischer Systeme zu
beschreiben versucht.
Hierzu gehören z.B. die Beschreibung der
Bewegung und des inneren mechanischen
Zustands von Körpern unter Einwirkung von
Kräften und Drehmomenten.
• Berechnung von Zahnbewegungen mit unterschiedlichen Rotationszentren
Koordinatensysteme, Vorzeichenkonventionen
Zur Beschreibung mechanischer Probleme werden
Koordinatensysteme
eingeführt.
+Z
+Y
+X
Referenzsystem sollte
immer das kartesische
Koordinatensystem sein:
rechtshändig, rechtwinklig
2
Problemorientierte Koordinatensysteme
Problemorientierte Koordinatensysteme
Es gibt verschiedene Systeme zur Beschreibung
kieferorthopädischer Zahnbewegungen oder Kraftsysteme.
Die kieferorthopädische
Realität ist weder rechtwinklig noch rechtshändig!
(z.B. in:
Graber / Swain:
Kieferorthopädie)
Vektoren
körpereigenes
System
Bei Kenntnis der Vorzeichenkonventionen und
der Orientierungen kann
man aber von einem
System ins andere
umrechnen.
ortsfestes
System
Vektoren
Zur Beschreibung der Bewegungen und der Kraftsysteme werden Vektoren benötigt. Im Gegensatz
zu Skalaren (Masse, Größenangaben) benötigen
diese sowohl die Angabe eines Betrages (Länge
des Vektors) als auch der Richtung im gewählten
System (Winkel bezüglich der Achsen).
()
Komponentena
schreibweise: A = b
c
a
b
c
|A| = a2 + b2 + c2
Vektoren
Kraft: linienflüchtig
Eigenschaften:
Die Kraft ist ein
gebundener, linienflüchtiger Vektor.
m = 100 kg
Die Wirkung ändert
sich nicht, wenn der
Angriffspunkt entlang der Kraftlinie
verschoben wird.
3
Vektoren: Drehmoment
Vektoren: Drehmoment
Ein Drehmoment M entsteht immer, wenn
eine Kraft F über einen Hebelarm r auf einen
Körper wirkt.
Moment einer Kraft,
reaktives Drehmoment
Kräftepaar,
reines
Drehmoment
Eigenschaften:
freier Vektor
Die Wirkung ändert sich also nicht, wenn
der Angriffspunkt beliebig verschoben wird.
Berechnung über das Kreuzprodukt:
M=
[
]
ry • Fz - rz • Fy
rz • Fx - rx • Fz
rx • Fy - ry • Fx
Vektoren: Drehmomente
Z
Kraftsystem:
X: mesio-distal
Y Y: oro-vestibulär
Z: koronal-apikal
X
d
d
f
r
r
M=RxF
r=10, d=5, F=1
0
R = -d
-r
F
F
F= 0
0
0
-d•0 + r • 0
M = -r•F - 0 • 0 = -10
5
0•0 + d • F
0
R = -d
-r
F
F = -f
0
-5
-d•0 - r • f
M = -r•F - 0 • 0 = -10
5
-0•f + d • F
WZ
WZ
F
Kraft- und Drehmomentschlüssiger Angriff (z.B. mit Loops)
f=0,5
Kraftsystem: Einheiten
Ein Kraftsystem besteht aus
drei Kräften und drei Drehmomente.
Dies entspricht i.a. der kieferorthopädischen
Situation.
Es gilt das SI: Système International mit
folgenden Einheiten für
die Kraft:
[N] = [kgm/s2]
das Drehmoment:
[Nm]
Möglichst Kräfte nicht in [g] angeben (das ist
eine Masse). Wenn schon, dann [p].
Die Wirkung von Kraftsystemen auf Körper
Starrer Körper:
Ein starrer Körper (wie ein Zahn) ändert seine
äußere Form bei Belastung nicht.
Freier starrer Körper, Schwerpunkt:
Auf einen freien starren Körper wirken keine
Lagerkräfte. Seine Bewegung wird in Bezug
auf den Schwerpunkt beschrieben. Beim freien
starren Körper ist dies der Massenmittelpunkt.
4
Translationen und Rotationen
Translationen und Rotationen
Greift eine einzelne Kraft am Körper und verläuft
die Kraftlinie durch den Schwerpunkt, so führt
dieser eine reine Translation aus:
F
)r
F
)S
Verläuft die Kraftlinie nicht durch den Schwerpunkt, so erfolgt zusätzlich eine Rotation:
S
S
S
M=r•F
Der Zahn als starrer Körper
Translationen und Rotationen
Ein einzelnes Drehmoment (das durch ein
Kräftepaar erzeugt wird) führt stets zu einer
Rotation um den Schwerpunkt:
r
-F
Knochenanbau
F
Knochenabbau
S
M=r•F
Rotation
Der Zahn als starrer Körper
Durch seine Lagerung im Parodont kann ein
Zahn nicht mehr als freier starrer Körper
angesehen werden.
Der Zahn ist ein gestützter starrer Körper.
Die Bewegung ist als Folge der Wechselwirkungen von Zahn / Zahnhalteapparat mit
dem Kraftsystem zu beschreiben.
Translation
Das Widerstandszentrum
Bei einem gestützten Körper werden die
Bewegungsmöglichkeiten eingeschränkt. Art
und Einfluss der Lagerung müssen berücksichtigt werden. Daraus ergibt sich das
Widerstandszentrum.
F
S
)
WZ
}
1/2 Widerstands1/2
zentrum
5
Das Widerstandszentrum
Widerstandszentrum eines Eckzahns
Der Zahn ist ein starrer Körper:
Er ändert seine Form bei Belastung
nicht.
Auf einen freien starren Körper
wirken keine Lagerkräfte. Seine
F
Bewegung wird in Bezug auf den
Schwerpunkt (Massenmittelpunkt)
beschrieben.
Durch seine Lagerung im Parodont kann ein Zahn
nicht mehr als freier starrer Körper angesehen
werden. Auch hier müssen Art und Einfluß der
Lagerung berücksichtigt werden.
Beschreibung der Zahnbewegung
Die Lage des Widerstandszentrums ist abhängig von:
Form und Größe der
Zahnwurzel
Beschaffenheit des
umgebenden Gewebes
2/3
WZ
1/3
Für einen humanen Eckzahn
liegt es etwa bei 40% der
Wurzellänge
Der Kraftangriff erfolgt aber am Bracket!
Bewegungen werden
in Bezug auf das
Widerstandszentrum
beschrieben.
Es ist das Analogon
zum Schwerpunkt
des freien starren
Körpers.
F
Einzelne Kraft im
WZ: Translation
Translation
Das Rotationszentrum
Das Rotationszentrum
Translationen und Rotationen überlagern sich, es
resultiert eine allgemeine Bewegung:
+
RZ
r
F
Die Bewegung kann
durch Angabe
eines momentanen
Rotationszentrums
(RZ) charakterisiert
werden.
M=r•F
Kraft im Bracket:
Translation
reaktives Drehmoment:
Rotation
6
Festlegung des Rotationszentrums?
Kraftsysteme und Rotationszentren
Es muß stets die Wirkung
des am Bracket angreifenden Kraftsystems im
Widerstandszentrum
betrachtet werden.
Kann man die Lage des
Rotationszentrums
(und damit die Zahnbewegung)
Appliziertes Kraftsystem:
einzelne Kraft F im Bracket
r
Effektives Kraftsystem im
Widerstandszentrum:
einstellen?
WZ
F,M
F
Kraft F sowie
reaktives Drehmoment M
(M=r•F)
Beispiel: Reine Translation
Es wird zunächst die angestrebte Bewegung
betrachtet und das dafür notwendige Kraftsystem im WZ ermittelt:
körperliche Zahnbewegung
einzelne Kraft
Anschließend wird das hierzu äquivalente Kraftsystem im Bracket berechnet.
Das effektive Kraftsystem im WZ kann man mit Hilfe
des
Drehmoment/Kraft-Verhältnisses (M/F)
des verwendeten Behandlungselements einstellen.
Es berechnet sich aus dem Verhältnis von im Brakket appliziertem Drehmoment zur applizierten Kraft
und bestimmt damit die Lage des Rotationszentrums.
Dem reaktiven
Drehmoment
M=r•F
muß ein
aufrichtendes
Drehmoment
-M = -r • F
entgegenwirken.
8
‚Translation‘, körperliche Zahnbewegung
‚Translation‘, M/F=Br - WZ
Kraft am Bracket:
F
RZ
WZ
‘Zwei Kraftsysteme sind äquivalent, wenn sie
dieselbe Wirkung auf einen Zahn ausüben.’
r
effektives
Kraftsystem:
F (Kraft)
äquivalentes
Kraftsystem:
F (Kraft),
-M (Drehmoment)
Drehmoment am Bracket:
M=10•F
8
Drehmoment/Kraft-Verhältnis - M/F
RZ
WZ
Rotationszentrum im
Unendlichen
7
M/F=10: Translation
Distalisation:
Kippung:
4 mm
0°
Berechnung mit
Widerstandszentrum
Eckzahnretraktion
Distalisation:
Kippung:
4 mm
0,5°
FEM-Simulation
F=1N, M=10Nmm
Eckzahnretraktion
‚Unkontrollierte Kippung‘, M/F=0
Kraft am Bracket:
F
M/F=0: unkontrollierte Kippung
Distalisation:
Kippung:
4 mm
15°
Distalisation:
Kippung:
4 mm
20°
RZ
Drehmoment am Bracket:
M=0
Rotationszentrum im
unteren Wurzeldrittel
WZ
Berechnung mit
Widerstandszentrum
FEM-Simulation
F=1N, M=0
8
‚Kontrollierte Kippung‘, M/F< Br - WZ
Kraft am Bracket:
RZ
F
Drehmoment am Bracket:
M=5•F
WZ
Rotationszentrum an der
Wurzelspitze
M/F=5: kontrollierte Kippung
Distalisation:
Kippung:
4 mm
10°
Distalisation:
Kippung:
‚Wurzelbewegung‘, M/F> Br - WZ
4 mm
9°
Kraft am Bracket:
F
Drehmoment am Bracket:
Berechnung mit
Widerstandszentrum
FEM-Simulation
M=15•F
WZ
Rotationszentrum an der
Inzisalkante
RZ
F=1N, M=5Nmm
M/F=15: Wurzelbewegung
Mesialisierung:
Kippung:
0,3 mm
15°
Berechnung mit
Widerstandszentrum
Mesialisierung:
Kippung:
0,5 mm
15°
FEM-Simulation
F=1N, M=15Nmm
9
F=0: Rotation um das WZ
Kippung:
-15°
Kippung:
Berechnung mit
Widerstandszentrum
Molarenaufrichtung
-15°
FEM-Simulation
M=-10Nmm
Reine Rotation (RZ im WZ - Furkation)
Aktuelle biomechanische Probleme
• Kieferorthopädische Grundlagen (Wdh.):
WZ, RZ, M/F-Verhältnis
• Materialeigenschaften des Zahnhalteapparats
• Lage des Widerstandszentrums einwurzeliger Zähne
mehrwurzeliger Zähne
eines Frontzahnblocks
• Mathematisches Modell der Zahnbewegung
• Verifizierung an Hand klinischer Beispiele
• Berechnung von Zahnbewegungen mit unterschiedlichen Rotationszentren
Zahnbewegung durch Knochenumbau
Zahnbewegung und ‚Bone Remodeling‘
Initiale klinische Situation:
Anwendung von Kraftsystemen durch spezielle
orthodontische Federn
Knochenanbau
Klinische Endsituation
nach mehreren Wochen
oder Monaten der
Behandlung
Knochenabbau
Rotation
Translation
10
Zahnbewegung und ‚Bone Remodeling‘
Biomechanische Komponenten
Mathematische Methoden zur Berechnung von
Kräften und Zahnbewegungen.
Experimentelle Methode zur computergestützten
Vermessung kieferorthopädischer Modelle.
Dreidimensionale Darstellung der gemessenen
Zahnpositionen.
Initiale und finale
Konfigurationen
sind gleich
Festlegung des Rotationszentrums?
Grundlage zur Berechnung von Rotationszentren sind
experimentelle und theoretische Untersuchungen. Erste
Arbeiten hierzu wurden von Christiansen (1969) und
Burstone bzw. Pryputniewicz und Burstone (1979)
vorgestellt.
Es wurde eine Formel zur Berechnung des Rotationszentrums in Abhängigkeit vom Kraftsystem am Bracket
hergeleitet und experimentell verifiziert.
Programm zum Design kieferorthopädischer
Behandlungselemente (CAD).
‚Burstone‘-Formel
M/F=(0,068•h²)/Y
RZ
Y
M: Drehmoment am Bracket
F: Kraft am Bracket
h: Wurzellänge
h
Y: Position des
Rotationszentrums
WZ
Sie benutzten mathematisch-analytische Methoden.
Heutzutage werden überwiegend numerische Methoden,
wie z.B. die Finite Elemente Methode (FEM), eingesetzt.
Kernpunkt: Geometrie der
Wurzel, also Lage des WZ!
Material-Parameter und WZ
Ausgangspunkt: E-Modul des PDL
Lage des Widerstandszentrums
bei unterschiedlicher
Wurzelkonfiguration
100000
E-Modul des PDL [MPa]
Materialeigenschaften
des Zahnhalteapparats
M,F
10000
1000
100
10
1
0,1
0,01
72
74
76
78
80
82
84
86
88
90
92
94
Jahreszahl der Veröffentlichung
11
Lage des WZ
Aufgaben
Bestimmung des Zusammenhangs aus einwirkendem
Das Widerstandszentrum eines Zahns ist der
wesentliche Parameter, der seine Bewegung
festlegt. Je nach Art der Unetrsuchung (zweidimensional / dreidimensional, analytisch, numerisch) schwanken die Positionen um ca. 10%.
Kraftsystem und resultierender initialer Zahnbewegung. Hieraus erhält man die benötigten Materialparameter, denn insbesondere das mechanische
Verhalten des PDL ist nicht eindeutig geklärt.
Burstone (1968) :
40 %
Davidian (1971) :
39 bis 44 %
Halazonetis (1996):
42 %
Vollmer et al. (1999):
42 % bzw.
Aufstellen eines geeigneten Rechenmodells zur
Bestimmung der Deformationen und Belastungen.
Neuberechnung des Widerstandszentrums
einwurzeliger Zähne.
37 %
Messung initialer Zahnbewegung
Mobilitäts-Mess-System MOMS
Die initiale Zahnbewegung zeigt
nichtlineares Verhalten.
Flächen-Sensoren zur
Positionsmessung
3
2
SteuerComputer
6-AchsenPositionierComputer
6-AchsenPositionierTisch
Rotation
Ry
A/D Converter
SensorComputer
3D-Kraft/
Drehmoment-Sensor
Translation
Tx
PSD Verstärker
4/00
0,8
0,7
Rotation [°]
Translation [mm]
0,6
3D - Messtisch zur
Belastung mit Kräften /
Drehmomenten
0,5
0,4
0,3
0,2
1
Präparat mit LaserDioden und LinsenSystem
0,1
Auflösung / Genauigkeit
0
0,0
0,5
1,0
1,5
2,0
2,5
-0,1
Kräfte:
0,01 N
Translationen: 0,01 mm
Kraft F [N]
Mobilitäts-Mess-System MOMS
Drehmomente:
0,5 Nmm
Rotationen:
0,022°
Die Finite Elemente Methode (FEM)
Flächensensoren
Zerlegung einer
Laser-KoordinatenSystem
Struktur in eine
Vielzahl endlich
großer 'finiter'
Elemente. Jedes
Element verhält sich
wie ein Teil eines
Positioniertisch
Kraft / Drehmoment-Sensor
Deformationen
im Modell
Knochens oder
Kräfte
Zahns.
Eckzahnpräparat
12
Kraftsystem an der Zahnkrone
Vollständiges
FE-Modell
Fx
FE-Modelle humaner Eckzähne
Insgesamt 8 Präparate einwurzeliger Zähne
(Eck- und Schneidezähne).
Materialeigenschaften des PDL
Mittelwerte und Standardabweichungen aus den
Rechnungen zu 8 Präparaten:
E1 = 0,05 (02) MPa
E2 = 0,27 (12) MPa
Materialeigenschaften
Dentin:
20 GPa
Schmelz:
80 GPa
Kortikalis:
20 GPa
Spongiosa:
3 GPa
Querkontraktion:
0,3
Bislang isotrop,
isotrop, homogen und linear!
Materialparameter und ihre Bedeutung
Die initiale Bewegung von Zähnen läßt sich im
Finite Elemente-Modell mit guter Genauigkeit
berechnen.
Das nichtlineare elastische Verhalten des PDL
läßt sich durch eine Bilinearität annähern.
Die Zahnauslenkung wird überwiegend durch
das Verhalten des PDL bestimmt.
εG = 7,5 (2,4) %
13
Grund für das bilineare Verhalten
Anordnung der parodontalen Fasern?
Berchnung der Lage von
Widerstandszentren
bei einwurzeligen Zähnen
Ausgangspunkt: Lage des WZ
Burstone (1968) :
40 %
Davidian (1971) :
39 bis 44 %
Halazonetis (1996):
42 %
Vollmer et al. (1999):
42 % bzw.
FE-Modelle von Front- und Eckzähnen
37 %
Mit den entwickelten FE-Modellen kann die
individuelle Position des WZ durch Aufbringen
eines einzelnen Drehmomentes ermittelt werden.
Lage der Widerstandszentren bei 8 Präparaten
2_01 My
2_01 Mx
3_00 My
1_99 My
3_00 Mx
1_98 My
1_99 Mx
1_98 Mx
2_98 My
2_98 Mx
4_00 Mx
4_00 My
2_00 My
2_00 Mx
zervikal
apikal
x
5_00 My
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
5_00 Mx
Höhe des PDL [mm]
Lage des Widerstandszentrums relativ zur
Alveolenhöhe
Präparat Nr.
14
Schlussfolgerungen
Burstone (1968) :
40 %
Davidian (1971) :
39 bis 44 %
Halazonetis (1996):
42 %
Vollmer et al. (1999):
42 % bzw.
Diese Untersuchung (2002):
43 %
37 %
]
[m
ltio
s
n
ra
T
Bisherige Untersuchungen zur Lage des WZ einwurzeliger Zähne können gut bestätigt werden,
obwohl diese oftmals mit idealisierten Geometrien
berechnet wurden.
Berchnung der Lage von
Widerstandszentren
von Prämolaren und Molaren
FE-Modelle von Molaren
Kräftepaar
Insgesamt 5 Modelle von Präparaten
extrahierter unterer Molaren
Kräftepaar
15
Lage der Widerstandszentren bei 5 Molaren
FE-Modelle von Prämolaren
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
x
Sagittalebene
zervikal
apikal
Frontalebene
Lage der Bifurkation
zervikal
apikal
Insgesamt 5 Modelle von Präparaten
extrahierter, zweiwurzeliger Prämolaren
Kräftepaar
Kräftepaar
Lage der WZ bei 5 Prämolaren
Lage des Widerstandszentrums relativ
zur Alveolenhöhe
Höhe des PDL [mm]
Höhe des PDL [mm]
Lage des Widerstandszentrums relativ
zur Alveolenhöhe
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
x
Sagittalebene
zervikal
apikal
Frontalebene
Lage der Bifurkation
zervikal
apikal
16
Schlussfolgerungen
Schlussfolgerungen
Die Widerstandszentren der Molaren lagen im
Mittel bei 44 (6) Prozent der Wurzellängen in
Richtung Apex, während die Bifurkationen bei 31
Prozent der Wurzellängen lagen.
Sie liegen damit deutlich weiter in Richtung
Wurzelspitze als in früheren Untersuchungen
angegeben.
]
[m
ltio
s
n
ra
T
Durchschnittliche Lage der
Durchschnittliche Lage der
Widerstandszentren [%]
Bifurkationen [%]
Molaren
44 (6)
31
Prämolaren
40 (6)
47
Bei den Prämolaren lagen die WZ im Mittel bei 40
(6) Prozent, die Bifurkationen bei 47 Prozent der
Wurzellängen in Richtung Apex.
]
[m
ltio
s
n
ra
T
Insgesamt liegen die Widerstandszentren sowohl
der Molaren als auch der Prämolaren sehr nahe
bei denen einwurzeliger Zähne, und scheinen nur
schwach von der Lage der Furkation abzuhängen.
Ausgangspunkt
Rechnerisch und experimentell konnte dieses
Problem bislang noch nicht gelöst werden!
Lage des
Es existieren lediglich
‚Plausibilitätsüberlegungen‘,
Widerstandszentrums
die auf klinischen Beobachtungen beruhen.
eines Frontzahnblocks
Biomechanik der Retraktion der OK-Front
Einige Autoren haben auch versucht, mittels
Hebelgesetzen aus der Überlagerung der WZ der
einzelnen Zähne die Position des WZ des
gesamten Zahnblocks herzuleiten.
Kraftsystem zur Retraktion der OK-Front
WZ
L
F
intr
d
F
dist
Lage des Widerstandszentrums:
M
Loop
L = 9 - 10 mm apikal und
d = 7 mm distal
des Kraftangriffspunkt
F
dist
Es wirkt ein kippendes Moment auf die Front: Mkipp= Fdist • L
Gesamtes aufrichtendes Drehmoment: M = MLoop + Fintr • d
17
Kraftsystem zur Retraktion der OK-Front
anteriores Segment:
35° Angulation
Frontretraktion mit NiTi-T-Loop
posteriores Segment:
25° Angulation
Zustand nach ca. 8 Wochen
Okklusale Ansicht (initial)
Okklusale Ansicht (final)
Schlussfolgerungen
Obwohl die experimentelle Überprüfung die
Korrektheit des Kraftsystems bestätigt hat, ist die
Bewegung nicht zufriedenstellend verlaufen.
Die Lage des Widerstandszentrums eines
Zahnblocks scheint damit bislang noch nicht
eindeutig geklärt zu sein.
]
[m
ltio
s
n
ra
T
18
Finite Elemente Modell - Ergebnisse
Lage des Widerstandszentrums:
Finite Elemente Modell - Ergebnisse
Lage des Widerstandszentrums:
L
F
d
In der Literatur:
F
Neu berechnet:
L = 9 - 10 mm apikal und
L = 9 bzw. 12 mm apikal und
d = 7 mm distal
d = 5 mm distal
des Kraftangriffspunkt
des Kraftangriffspunkt
Finite Elemente Modell - Ergebnisse
Das Widerstandszentrum befindet sich in einer Ebene, aber...
Finite Elemente Modell - Ergebnisse
Lage des Widerstandszentrums:
~3 mm
~2,5 mm
~9 mm
~8,4 mm
Es gibt KEIN gemeinsames
Widerstandszentrum!
Verblockt mit: a) 0,46 mm x 0,64 mm
Stahldraht
b)1,38 mm x 1,92 mm
19