MEED02

Arithmetik
4. Die natürlichen Zahlen
1M
n  M  (n + 1)  M
1M
(4.1)
n  M  (n + 1)  M
(4.2)
Erfüllt M (4.1) und (4.2), so gilt   M
(4.3)
Carl Friedrich Gauß (1777 - 1855)
1
+
2 + 3 + ... + 100
100 + 99 + 98 + ... +
= 5050
1
101 + 101 + 101 + ...+ 101
1 + 2 + 3 + ... + n = n(n+1)/2
= 10100
4.2 Der binomische Satz
Die binomische Formel: (a + b)2 = 1a2 + 2ab + 1b2
(a + b)2 =
Binomialkoeffizienten
(a + b)n =
n n 0
  a b
0
 2
 
0
= 1,
+  n  an-1b1 +
 1
 2 2 0
  a b
0
 2
 
 1
+
 2 1 1
  a b
 1
= 2 und
 n  n-2 2
b
  a
 2
 2
  =
 2
+ ... +
+
 2 0 2
  a b
 2
1
n 0 n
  a b
n
 n 
n
 = n
  = 
 n - 1
 1
n
 
k 
=
n(n  1)(n  2)    (n  k  1)
1 2  3    (k  1)k
n n
  =   = 1
0 n
4.2 Der binomische Satz
n
 
 1
=
n
 
 2
= n(n  1)
1 2
n
 
3
=
n
1
n
  = n(n  1)(n  2)    (n  n  1)
1 2  3    (n  1)n
n
n(n  1)(n  2)
1 2  3
usw.
n
 
k 
n(n  1)(n  2)    3  2  1
=
1 2  3    (n  2)(n  1)n
 n 
n
 = n
  = 
 n - 1
 1
=
n(n  1)(n  2)    (n  k  1)
1 2  3    (k  1)k
n n
  =   = 1
0 n
 n  1


 k 
=
 n 


 k - 1
+
n
 
k 
Pascalsches Zahlendreieck
n=0
1
n=1
1
n=2
1
n=3
1
n=4
n=5
n
n
  k 
k 0
1
1
= 2n
5
1
2
3
4
1
3
6
10
Blaise Pascal
(1623 - 1662)
1
4
10
1
5
1
denn (a + b)n liefert genau 2n Produkte.
4.1 Man berechne die Binomialkoeffizienten
3
 
2
7
 
5
 10 
 
8
 49 
 
 6
5. Erweiterungen der Zahlenmenge
Die natürlichen Zahlen sind zwar abgeschlossen unter
Addition und Multiplikation, denn für n, m   ist (n + m) 
 und (nm)  . Dagegen ist n - m und n/m nicht immer
eine natürliche Zahl.
5.1 Die ganzen Zahlen
Die Erweiterung zu den ganzen Zahlen geschah im 13.
Jahrhundert, im Zeitalter des aufblühenden Bankwesens,
durch Leonardo von Pisa über die Interpretation von negativen
Zahlen als Schulden.
 = { ..., -3, -2, -1, 0, 1, 2, 3, ... }
Leonardo von Pisa
(1170 - 1240)
= Fibonacci
Die Abbildung Absolutbetrag bildet die ganze Zahl x auf die
nicht negative Zahl |x| ab
|x| =
{
x falls x  0
- x falls x  0
x ≤ |x|
Cauchy-Schwarzsche Ungleichung
|x + y| ≤ |x| + |y|
5.3 Die rationalen Zahlen
a c ad c b ad  c b
 


b d bd d b
bd
2 2/2 1


6 6/2 3
a c ac
 
b d bd
a c a d
/  
b d b c
Schon im 14 Jahrhundert hat Nicole von Oresme mit Hilfe von
Identitäten wie
43 = 64 = 82
sogar gebrochene Exponenten eingeführt
43/2 = 8
Vorsicht bei negativen Zahlen!
(-8) = (-2)3 = (-2)6/2 = 64 = 8
ist falsch. Grundsätzlich dürfen nur
positive Zahlen mit gebrochenen
Exponenten versehen werden.
Nicole von Oresme
(1323 - 1382)
103  10  10  10  1000
103  105  108 10x  10y  10x y
a
x
1
 x
a
a a
x
y
xy
a
x y
( xy )
a : a
y
( a ) : a
x
a x  ay  a x  y a  0
x y
a
 y
a
x
a a
x
x
a
x x
a
 x  1  a0
a
x
Wotans Ring Draupnir
t/s
Anzahl
t/s
10
Anzahl
Roms Staatsschulden nach Neros Tod (Sesterzen)
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
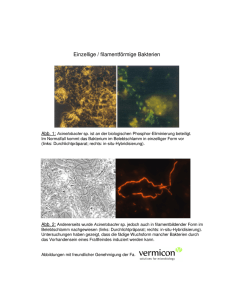
Bakterien im menschlichen Darm
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
4*1019 = 8!*12!*21137/2
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
22
Sterne im Weltall
4*1019 = 8!*12!*21137/2
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
22
Sterne im Weltall
34
Bakterien in den Erdmeeren
4*1019 = 8!*12!*21137/2
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
22
Sterne im Weltall
34
Bakterien in den Erdmeeren
38
größte von Menschenhand ermittelte Primzahl 2127-1
4*1019 = 8!*12!*21137/2
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
22
Sterne im Weltall
34
Bakterien in den Erdmeeren
38
größte von Menschenhand ermittelte Primzahl 2127-1
59
Sandkörnerzahl des Archimedes übertroffen
4*1019 = 8!*12!*21137/2
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
22
Sterne im Weltall
34
Bakterien in den Erdmeeren
38
größte von Menschenhand ermittelte Primzahl 2127-1
59
Sandkörnerzahl des Archimedes übertroffen
80
Protonen im Weltall
4*1019 = 8!*12!*21137/2
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
22
Sterne im Weltall
34
Bakterien in den Erdmeeren
38
größte von Menschenhand ermittelte Primzahl 2127-1
59
Sandkörnerzahl des Archimedes übertroffen
80
Protonen im Weltall
43 min
1000! übertroffen
4*1019 = 8!*12!*21137/2
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
22
Sterne im Weltall
34
Bakterien in den Erdmeeren
38
größte von Menschenhand ermittelte Primzahl 2127-1
59
Sandkörnerzahl des Archimedes übertroffen
80
Protonen im Weltall
43 min
?
1000! übertroffen
999
4*1019 = 8!*12!*21137/2
t/s
Anzahl
10
Roms Staatsschulden nach Neros Tod (Sesterzen)
11
Sterne in der Milchstraße
14
Bakterien im menschlichen Darm
20
Kombinationen des Rubikwürfels
22
Sterne im Weltall
34
Bakterien in den Erdmeeren
38
größte von Menschenhand ermittelte Primzahl 2127-1
59
Sandkörnerzahl des Archimedes übertroffen
80
Protonen im Weltall
43 min
1000! übertroffen
11 a 263 d 999
4*1019 = 8!*12!*21137/2
5.5 Die reellen Zahlen
2  a/b
2b2 = a2 ?
Jede Wurzel aus einer natürlichen Zahl, die nicht selbst eine
natürliche Zahl ist, kann nicht als Bruch dargestellt werden.
Man bezeichnet solche Zahlen als Irrationalzahlen.
=U
Die Gleichung
x2 = 2
besitzt zwei Lösungen, nämlich 2 und -2.