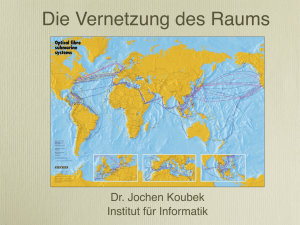
Voronoi-Diagramme

Voronoi-Diagramme
Kurze Einführung zum Thema
Voronoi-Diagramme und
deren Anwendungen
2
1.
2.
3.
4.
5.
Einführungsbeispiel
Definitionen
Delaunay Triangulierung
Algorithmen zur Berechnung des Diagramms
Anwendungen
3
1 Einführungsbeispiel
Grüne Fläche: Wald
Rote Punkte: Brandwachtürme
Frage: Welche Fläche muss jeder Brandwachturm überwachen?
4
1 Einführungsbeispiel
Antwort: Jeder Brandwächter überwacht die Bäume, die näher zu
seinem Turm sind, als zu jedem anderen.
Das „Voronoi-Diagramm“ zeichnet die Linien zwischen den Gebieten
5
2 Definitionen
Sei P = {p1, p2, ..., pn} Menge von Punkten auf einer 2-dim. Fläche.
Diese Punkte werden Orte (engl. sites) genannt.
Zerteilt man die Fläche indem man deren Punkte ihrem nächsten Ort pi
zuordnet, entstehen zu jedem Ort Voronoi-Regionen V(pi):
V(pi) = {x: | pi – x | ≤ | pj – x | für alle j ≠ i }
Manche Punkte werden mehr als einem Ort zugeordnet.
Die Menge aller dieser Punkte bildet das Voronoi-Diagramm V(P).
6
Voronoi-Diagramm für zwei Orte
Seien zwei Orte p1 und p2.
B12 ist die Mittelsenkrechte
zwischen p1 und p2.
Dann ist jeder Punkt x auf B12
gleich entfernt zu p1 und p2.
Nach dem Satz von Euklid ist |p1x| = |p2x|.
7
Voronoi-Diagramm für drei Orte
Seien p1, p2 und p3 drei Orte,
B12, B23 und B13 Mittelsenkrechten
und das Dreieck (p1, p2, p3)
Nach Euklid:
Die Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt.
=>Umkreismittelpunkt eines Dreiecks.
Beachte: Der Umkreismittelpunkt muss nicht im Dreieck liegen!
8
2.1 Halbebenen
Mehr als drei Orte:
Mittelsenkrechten Bij spielen auch hier entscheidende Rolle!
Unterteilung der Fläche in eine Halbebene H(pi, pj) mit der Grenze Bij und
dem Ort pi
=>Menge H(pi, pj) enthält die Punkte, die zu pi näher sind als zu pj.
V(pi) ist die Menge der Punkte, die näher zu pi sind als zu allen anderen Orten.
Oder auch:
V(pi) enthält die Punkte näher zu pi als zu p1 und
näher zu pi als zu p2 und
...
näher zu pi als zu pn.
9
2.1 Halbebenen
Daraus ergibt sich für V(pi) folgende Gleichung:
V(pi) = ∩i≠j H(pi, pj)
Diese Gleichung zeigt wichtige Eigenschaft der Voronoi-Diagramme:
Da der Durchschnitt von Halbebenen konvex ist, ist auch jede
Voronoi-Region V(pi) ein konvexes Polygon.
10
Die Kanten der Voronoi-Regionen heißen Voronoi-Kanten.
Alle inneren Punkte der Voronoi-Kanten haben zwei nächste Orte.
Die Knoten (Ecken) der Voronoi-Regionen heißen Voronoi-Knoten.
Alle Voronoi-Knoten haben mindestens drei nächste Orte.
11
Beispiel
Voronoi-Diagramm mit n = 20 Orten
12
2.2 Größe des Diagramms
Zur Vereinfachung: - keine vier Orte sind `kozirkular´
(d.h. nicht mehr als drei Orte liegen auf einem Umkreismittelpunkt)
=>jeder Voronoi-Knoten hat den Grad 3
Nun konstruieren wir einen ungerichteten Graphen G wie gefolgt:
- Die Knoten von G sind die Orte
- Zwei Knoten werden mit einer Kante verbunden, wenn ihre Voronoi-Regionen
sich eine Voronoi-Kante teilen.
13
2.2 Größe des Diagramms
Für unser Diagramm aus dem Einführungsbeispiel ergibt sich folgender Graph(blau):
14
2.2 Größe des Diagramms
- alle Punkte (Orte) sind verbunden
-G ist ein ‚triangulärer‘ Graph
(da alle Voronoi-Knoten Grad 3 haben)
Nach Euler hat ein triangulärer Graph mit n Knoten
max. 3n-6 Kanten und besteht aus max. 2n-4 Flächen.
Da
und
folgt:
#Flächen von G = #Voronoi-Knoten
#Kanten von G = #Voronoi-Kanten,
#Voronoi-Knoten = O(n)
#Voronoi-Kanten = O(n)
15
2.2 Größe des Diagramms
Ohne Einschränkung der Voronoi-Knoten auf Grad 3:
Komplexität der Voronoi-Diagramme bleibt bei O(n), da
nicht-trianguläre Graphen weniger Knoten und weniger Kanten haben.
Als Folgerung aus max. 3n-6 Kanten kann man sagen, dass die
durchschnittliche Anzahl der Voronoi-Kanten eines Polygons nicht mehr als
sechs sein kann.
16
3 Delaunay Triangulierung
In 1934 zeigt Delaunay, dass der vorher beschriebene ungerichtete
Graph G eine Triangulierung der Orte P eines Voronoi-Diagramms
ist (falls jeder Voronoi-Knoten vom Grad 3 ist).
Dies nennt man die Delaunay Triangulierung D(P).
17
3 Delaunay Triangulierung
In 1934 zeigt Delaunay, dass der vorher beschriebene ungerichtete
Graph G eine Triangulierung der Orte P eines Voronoi-Diagramms
ist (falls jeder Voronoi-Knoten vom Grad 3 ist).
Dies nennt man die Delaunay Triangulierung D(P).
18
Eigenschaften der Delaunay Triangulierung
D1. D(P) ist der ungerichtete duale Graph zu V(P). (siehe Def.)
D2. D(P) ist eine Triangulierung, wenn keine vier Punkte `kozirkular´ sind:
Jede Fläche ist ein Dreieck. Das ist der Satz von Delaunay. Die Flächen von D(P)
nennt man Delaunay Dreiecke.
D3. Jedes Dreieck von D(P) entspricht einem Knoten von V(P).
D4. Jede Kante von D(P) entspricht einer Kante von V(P).
D5. Jeder Knoten von D(P) entspricht einer Region von V(P).
D6. Die Ränder von D(P) ergeben die konvexe Hülle der Orte.
D7. Das Innere jedes Dreiecks von D(P) enthält keine Orte.
19
Eigenschaften der Voronoi-Diagramme
V1. Jede Voronoi-Region V(pi) ist konvex.
V2. V(pi) ist unbegrenzt, wenn pi auf der konvexen Hülle der Menge P liegt.
V3. Wenn v ein Voronoi-Knoten am Verbindungspunkt von V(p1), V(p2) und V(p3)
ist, dann ist v der Mittelpunkt des Kreises C(v) auf dem p1, p2 und p3 liegt.
V4. C(v) ist der Umkreis des zu Voronoi-Knoten v gehörenden Delaunay Dreiecks.
V5. Das Innere von C(v) enthält keine Orte.
V6. Wenn pj der `nächste Nachbar´ von pi ist, dann ist (pi, pj) eine Kante von D(P).
V7. Wenn es einen Kreis durch pi und pj gibt welcher keine anderen Orte enthält,
dann ist (pi, pj) eine Kante von D(P).
(Aus Umkehrung folgt: Für jede Delaunay-Kante gibt es leere Kreise.)
20
Eigenschaften der Voronoi-Diagramme
21
Eigenschaften der Voronoi-Diagramme
Beweis zu V7.:
Behauptung: ab ist Delaunay-Kante gdw. es einen leeren Kreis durch a und b gibt:
D.h. dieser Kreis enthält weder im Inneren noch auf dem Rand einen anderen Ort
außer a und b.
Beweis: „=>“
ab ist Delaunay-Kante
=> V(a) und V(b) teilen eine Kante e
Nun bildet man einen Kreis C(x) mit Mittelpunkt x, der im Inneren(!) der Kante e
liegt und durch a und b geht. Dieser Kreis ist leer!
Angenommen der Punkt c ist im oder auf dem Kreis
=> x ist auch in V(c)
=> Widerspruch zu x nur in V(a) und V(b) !
22
Eigenschaften der Voronoi-Diagramme
„<=“
Angenommen es gibt einen leeren Kreis C(x) durch a und b mit Mittelpunkt x
x ist gleichweit zu a und b
x ist in V(a) und V(b), solange kein Ort kommt, die näher ist als a und b. Dies
ist aber nicht möglich, da der Kreis leer sein soll!
x ist im Durchschnitt von V(a) und V(b).
x liegt auf der Voronoi-Kante (Untermenge von Bab) zwischen V(a) und V(b)
ab ist Element von D(P)
q.e.d.
23
4 Algorithmen zur Berechnung des
Voronoi-Diagramms
24
4.1 Durchschnitt von Halbebenen
Man kann jede Voronoi-Region bilden indem man den Durchschnitt von n - 1
Halbebenen nach der Gleichung
V(pi) = ∩i≠j H(pi, pj)
bildet.
(Zur Erinnerung: H ist die Fläche zum Ort, die von der Mittelsenkrechten
begrenzt wird.)
Durchschnitt von n Halbebenen ist gleich der Arbeit beim Erstellen einer
2-dimensionalen konvexen Hülle von n Punkten und kann mit ähnlichen
Algorithmen in O(n log n) Zeit erledigt werden.
Bei n Voronoi-Regionen ist der Gesamtaufwand O(n2 log n).
25
4.2 Inkrementelle Konstruktion
Angenommen: Voronoi-Diagramm V mit k Orten ist berechnet
Wir wollen ein Diagramm V´ erstellen, nachdem wir den Ort p hinzugefügt haben.
Angenommen: p fällt in das Innere eines (bisher Ort-freies) Kreises C(v) mit
Voronoi-Knoten v als Mittelpunkt.
=>v kann nicht mehr Voronoi-Knoten von V´ sein
(wegen Bedingung V5: das Innere von C(v) enthält keine Orte)
=>alle Knoten, die aus V entfernt werden müssen.
Es ergibt sich ebenfalls, dass alle auf eine bestimmte Fläche des Diagramms
begrenzt sind.
Green & Sibson 1977 entwickelten daraus Algorithmus, der das Einsetzen eines
Ortes in O(n) schafft.
=> Gesamtlaufzeit von O(n2).
26
4.3 Divide & Conquer
Voronoi-Diagramme können mit komplexen divide-and-conquer Algorithmus in
O(n log n) Zeit erstellt werden
Die Komplexität von O(n log n) ist asymptotisch optimal
ABER: dieser Algorithmus ist sehr schwer zu implementieren
27
4.3 Divide & Conquer
28
4.4 Fortune‘s Algorithmus
Bis Mitte der 80er Jahre: meistens inkrementeller Algorithmus(4.2)
(wegen komplexer Implementierung mit divide-and-conquer)
In 1985 entwickelte Fortune plane-sweep Algorithmus
Vorteile:
-einfacher als der inkrementelle Algorithmus
-im schlechtesten Falle Komplexität O(n log n)
Die Grundidee:
Eine sweep-Linie durchläuft eine Fläche.
Für den bereits passierten Abschnitt steht die Lösung schon fest, für den Rest noch
nicht.
29
4.4 Fortune‘s Algorithmus
Vorbemerkung 1: Kegel
Seien Orte p1 und p2 auf xy-Ebene eines 3-dim. Koordinatensys.
Über jedem Ort sei Kegel mit Gipfel in p mit Seitenneigung 45°
Diese schneiden sich in Kurve im Raum.
Diese Kurve liegt auf vertikalen Ebene.
Durch diese Ebene kann man Schnitt auf
xy-Ebene projizieren.
Der Schnitt ist die Voronoi-Kante zwischen p1 und p2.
30
4.4 Fortune‘s Algorithmus
Vorbemerkung 2: Schnitt durch die Kegel
Wir durchlaufen alle Kegel mit 45° zur xy-Ebene geneigten Ebene π
sweep-Linie L ist Schnitt von π und xy-Ebene
L sei parallel zur y-Achse
(mit x-Koordinate l)
31
4.4 Fortune‘s Algorithmus
Stellen wir uns nun vor π sowie alle Kegel seien undurchsichtig und wir schauen
nun von unten (z = -∞) herauf:
-Rechts von L (x > l) sehen wir nur die Unterseite von π, weil sie die xy-Ebene
schneidet und die Orte mit deren Kegeln verdeckt.
-Der Schnitt von π und jedem Kegel ist eine Parabel.
32
4.4 Fortune‘s Algorithmus
An den Stellen wo zwei Parabeln sich treffen, trifft π zwei Kegel.
Aus Vorbemerkung 1 => an diesen Stellen muss Voronoi-Kante sein
33
4.4 Fortune‘s Algorithmus
Parabolische Front
Da π die selbe Neigung (45°) wie die Kegel hat
=>sweep-Linie L trifft den Ort p genau dann, wenn π den Kegel von p zum ersten
mal berührt.
Nun muss nur die „parabolische Front“ beobachtet werden
(=Schnitt der Kegel mit π)
An den „Knicken“ist eine Voronoi-Kante.
34
4.4 Fortune‘s Algorithmus
Wir müssen nur den Verlauf der parabolischen Front abspeichern, um daraus das
Voronoi-Diagramm zu erstellen.
Die Komplexität der Größe um die Front zu speichern ist O(n)
(oft nur O(√n))
=>Großer Vorteil des Fortune Algorithmus:
Bei großem n ist die Größe des Gespeicherten oft viel kleiner als das des
Diagramms.
Bemerkung: n ist oft groß!
(z.B. 106 bei geographischen Informationssystemen)
35
5 Anwendungen
36
5.1 Nächster Nachbar
Nun suchen wir den „nächsten Nachbarn“ zu jedem Punkt in einer
gegebenen Menge.
Definition der „nächster Nachbar“-Relation:
b ist ein nächster Nachbar von a gdw. |a – b| ≤ minc≠a|a – c|
Schreibweise: a → b
Diese Relation ist nicht symmetrisch!
(hier: a → b, aber nicht b → a)
Ein Punkt kann mehrere nächste
Nachbarn haben!
(hier: Punkt d)
37
Nächste Nachbar Anfragen
Gegeben: Menge P von Punkten(Orten) und deren Voronoi-Diagramm.
Nun brauchen wir für einen neuen Anfragepunkt q nur noch herausfinden in
welcher(n) Voronoi-Region(en) er liegt.
Die zu diesen Voronoi-Regionen zugehörigen Orte sind nächste Nachbarn von q.
Jede Anfrage kann in O(log n) Zeit erledigt werden!
38
Alle Nächsten Nachbarn
Definieren wir den Nächster-Nachbar-Graph (NNG) um jedem Punkt der
Menge P mit seinem nächsten Nachbarn zu verbinden.
NNG ist ungerichtet definiert (obwohl Relation nicht symmetrisch ist)
=> Lemma:
NNG ist Teilmenge von D(P) (= Delaunay Triangulierung)
Ein primitiver Algorithmus würde O(n2) benötigen.
Durch unser Lemma wissen wir, dass wir nur die O(n) Kanten der Delaunay
Triangulierung von P durchsuchen müssen.
=> Gesamtlaufzeit O(n log n).
39
Alle Nächsten Nachbarn
40
5.2 Größter Leerer Kreis
Zum Beispiel folgende Anwendung:
-Wenn die Orte Filialen einer Firma sind, ist die Mitte des größten leeren
Kreises der optimale Ort für das Errichten einer neuen Filiale.
Eigentlich Unsinn größten Kreis zu suchen da außerhalb jeder Menge unendlich
große leere Kreise sind.
Deshalb fassen wir das Problem so auf:
Größter Leerer Kreis: Finde einen größten leeren Kreis dessen Mitte in der
konvexen Hülle der Menge S von n Orten ist. Leer, so dass er kein Ort im
Inneren hat. Größter, so dass kein anderer solcher Kreis besteht der einen
echt-größeren Radius hat.
41
5.2 Größter Leerer Kreis
Mittelpunkte innerhalb der Hülle
Angenommen p ist streng im Inneren der Hülle H und der Kreis geht genau
durch ein Ort s1.
42
5.2 Größter Leerer Kreis
Mittelpunkte innerhalb der Hülle
Angenommen p ist streng im Inneren der Hülle H und der Kreis geht genau durch
zwei Orte s1 und s2.
43
5.2 Größter Leerer Kreis
Mittelpunkte innerhalb der Hülle
der Kreis geht durch drei Orte
Da aber die Mitte eines solchen Kreises genau auf einem Voronoi-Knoten liegt,
folgt daraus:
Lemma 1: Wenn die Mitte p eines größten leeren Kreises streng im Inneren der
konvexen Hülle H aller Orte S liegt, dann muss p auf einem Voronoi-Knoten
liegen.
44
5.2 Größter Leerer Kreis
Mittelpunkte auf der Hülle
Den Fall, dass p auf einem Knoten der Hülle liegt, können wir ausschließen, da
diese immer ein Ort sind (Def. Hülle H).
p liegt auf der Kante h von H
Angenommen der Kreis
um p geht durch
genau ein Ort s1.
45
5.2 Größter Leerer Kreis
Mittelpunkte auf der Hülle
=> der Kreis geht durch zwei Orte
Dann ist p aber auch auf einer Voronoi-Kante. Daraus folgt:
Lemma 2: Wenn die Mitte p eines größten leeren Kreises auf der konvexen Hülle
H aller Orte S liegt, dann muss p auf einer Voronoi-Kante liegen.
46
5.2 Größter Leerer Kreis
Algorithmus
Nun sind wir kurz vor dem Ziel. Wir haben eine endliche Menge von möglichen
Punkten, die Mitten des größten leeren Kreises sein könnten:
Voronoi-Knoten
Schnittpunkte der Voronoi-Kanten mit der Hülle der Orte
Bemerkung: Nicht alle Voronoi-Knoten liegen zwangsweise in der Hülle! Nach
unserer Definition vom größten leeren Kreis kommen diese Knoten nicht als
Mitten in Betracht. Dieses muss im Algorithmus beachtet werden!
Zur Laufzeit:
-Test, ob ein Voronoi-Knoten in Hülle liegt: O(log n) (siehe Kapitel 7 im Buch).
-Schnitt Voronoi-Kanten mit Hülle: O(log n)
=>Gesamtlaufzeit O(n log n).
47
5.2 Größter Leerer Kreis
Algorithmus: GRÖßTER LEERER KREIS
Berechne das Voronoi-Diagramm V(S) der Orte S.
Berechne die konvexe Hülle H der Orte S.
for alle Voronoi-Knoten v do
if v ist im Inneren von H then
Berechne den Radius des Kreises mit Mittelpunkt v
und bringe max auf den neusten Stand.
for alle Voronoi-Kanten e do
Berechne den Schnittpunkt p zwischen e und der Hülle.
Berechne den Radius mit Mittelpunkt p
und bringe max auf den neusten Stand.
Gebe max zurück.
48