Folien zur Vorlesung (Powerpoint 7.697 kb)


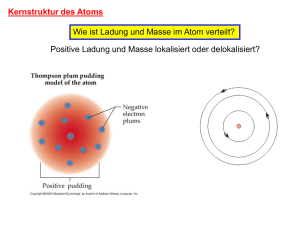
d
d*sin()
Bragg Bedingung für konstruktive Interferenz:
2d sin() = m * 
Wellenlänge
Gitterabstand
Ganze Zahl
3: Kann man Atome sehen????
3.1: Wie gross sind Atome
3.1.1. Bestimmung aus dem Kovolumen:
3.1.2. Röntgenbeugung an Kristallen (Bragg, s.o.)
3.1.3. Über Gasstreuung: Wirkungsquerschnitt
3.2 Licht von (einzelnen) Atomen (Falle)
3.3 Spuren von Atomen (Nebelkammer)
3.4 Abtasten (Rastertunnelmikroskop)
This is the stretch mode for 7 ions (also called breathing mode). The frequency
of this mode is 185 kHz. The corresponding center-of-mass mode has a
frequency of about 107 kHz. You can see that to some extend the center-ofmass mode has also been excited.
Center-of-mass mode. The oscillation amplitude is rather high. On the left the
ions already leave the laser beam. The whole chain of ions has a length of
about 85 micrometers, i.e. the average ion-ion distance is 14 micrometers.
http://heart-c704.uibk.ac.at/oscillating_ions.html
Quantum Optics and Spectroscopy
Institut für Experimentalphysik, Universität Innsbruc
Wie „fängt“ man einzelne Ionen??
Paul Falle
Penning Falle
-> Montag!
3.3 Spuren von Atomen/Ionen in Nebelkammern
Teilchen
(Heliumkerne)
Stoß
Mit Magnetfeld
www.nobel.se
http://www.unibas.ch/physikdidaktik/TEILCHEN_97/EXPTEST.HTML
•Verschiebung mit Piezos
3 Dimensional
•Dämpfung!!!
•Messung des Tunnelstroms
(wird konstant gehalten durch
Höhenvariation)
Fehlstelle
Siliziumoberfläche STM Aufnahme
Atome nicht nur sehen, sondern einzeln manipulieren:
Einzelne Xenon Atome, bei –273K (IBM 1989)
C60 Moleküle als „Rechenschieber“ (1996)
3: Kann man Atome sehen????
3.1: Wie gross sind Atome
3.1.1. Bestimmung aus dem Kovolumen:
3.1.2. Röntgenbeugung an Kristallen (Bragg, s.o.)
3.1.3. Über Gasstreuung: Wirkungsquerschnitt (Folie)
3.2 Licht von (einzelnen) Atomen (Falle)
3.3 Spuren von Atomen (Nebelkammer)
3.4 Abtasten (Rastertunnelmikroskop)
4. Isotopie und Massenbestimmung
4: Isotopie und Massenbestimmung
Periodensystem (1869 Mendelejew, Lothar Meyer)
Sortiert nach periodisch wiederkehrenden chemischen&physikalischen
Eigenschaften
Hassium (von Hessen!)
Bei GSI entdeckt
Seltene Erden
Actinide
Ionisationsenergie
Edelgase: He, Ne, Ar, Kr, Xe
Ordnungszahl
Quelle: http://www.monroecc.edu/wusers/flanzafame/PeriodicFigs.htm
4: Isotopie und Massenbestimmung
Nichtganzahlige Massen: Mittelwert der verschiedenen Isotope
d.h. verschiedener Anzahl von Neutronen
Massenspektrometer:
1) Erzeuge geladene Teilchen:
z.B. Elektronenstoßionisation (beschleunige Elektronen
die Ionisieren, erzeugt Plasma, siehe Leuchtstoffröhre)
Laserfeld: Feldionisation
2) Analysiere q/m durch
elektrische Felder
magnetische Felder
Flugzeit
zeitabhängige Felder
Lorentzkraft:
F = q * (v x B)
Elektrisch:
F=q*E
!Geschwindigkeitsabhängig
Massenspektrometer:
Geladene Teilchen (Ionen) in elektrischen, magnetischen Feldern
Lorentzkraft:
F = q * (v x B)
Elektrisch:
F=q*E
!Geschwindigkeitsabhängig
Kraft senkrecht auf Bewegungsrichtung
-> Kreisbahn
radius = m/q * v / B
zu bestimmen
Massenspektrometer:
Geladene Teilchen (Ionen) in elektrischen, magnetischen Feldern
Lorentzkraft:
F = q * (v x B)
Elektrisch:
F=q*E
!Geschwindigkeitsabhängig
Ionenquelle
m/q Auflösung durch v begrenzt
radius = m/q * v / B
Aston 1919 „Geschwindigkeitsfocussierung“
Aston: gekreuzte E und B Felder
Ziel: verschiedene Geschwindigkeiten auf gleichen Punkt
geschickte Kombination von E und B
Ablenkung im B Feld
tan() = q B L / mv
Ablenkung im E Feld:
tan() = q E L / mv2
L
verschiedene Startwinkel
Richtungsfokussierung “Sektorfeld”
Massenspektrometrie:
Massenzahl 20!
19.9876 – 20.0628
Die Bewegung geladener
Teilchen in der
Sonnenatmosphäre
wird durch die
Sonnenmagnetfelder
mitbestimmt.
http://sohowww.estec.esa.nl/
Massenspektrometrie immernoch aktuell:
"for their development of
soft desorption ionisation methods
for mass spectrometric analyses
of biological macromolecules"
Ionisiere biologische Moleküle
ohne sie zu zerbrechen!
Quadrupol Massenspektrometer
Wolfgang Paul
1913-1993
Nobelpreis
1989
Wechselfelder
Näheres: Montags Ergänzungen
3: Kann man Atome sehen????
3.1: Wie gross sind Atome
3.1.1. Bestimmung aus dem Kovolumen:
3.1.2. Röntgenbeugung an Kristallen (Bragg, s.o.)
3.1.3. Über Gasstreuung: Wirkungsquerschnitt (Folie)
3.2 Licht von (einzelnen) Atomen (Falle)
3.3 Spuren von Atomen (Nebelkammer)
3.4 Abtasten (Rastertunnelmikroskop)
4. Isotopie und Massenbestimmung
5. Kernstruktur des Atoms
Rutherfordstreuung
differentieller Wirkungsquerschnitt
5: Kernstruktur des Atoms
Wie ist Ladung und Masse im Atom verteilt?
Positive Ladung und Masse lokalisiert oder delokalisiert?
5: Kernstruktur des Atoms
Betrachte die STREUUNG geladener Teilchen
“Streuwinkel”

“Stoßparameter” b
5: Kernstruktur des Atoms
“Streuwinkel”

“Stoßparameter” b
Z1Z2 e2
b=
4o 2mv2 sin2(/2)
für Coulomb Abstoßung zwischen Punktteilchen
5: Kernstruktur des Atoms
“Streuwinkel”

“Stoßparameter” b
Z1Z2 e2
Kann nicht
b=“Zielen” d.h. kenne b nicht
2 sin2(/2)
 ist die 4
einzige
o 2mv Messgrösse
“Schrotgewehr”
Was ist ein Wirkungsquerschnitt (differentieller Querschnitt) (2):
Bsp: Wald
„Fläche auf der die Wirkung Eintritt (z.B. Stoß)“
Nreaktion = Nprojektil Ftarget 
Nprojekti
l
Zufällige Verteilung aller
Stoßparameter
„Flächendichte“ (Teilchen/cm2)“
des Targets
 ist proportional zur Wahrscheinlichkeit
daß eine Reaktion Eintritt, wenn man
“zufällig” (alle Stoßparameter) bestahlt.
http://www.didaktik.physik.uni-erlangen.de/grundl_d_tph/exp_stoss/stoss_streu_3.html
Was ist ein Wirkungsquerschnitt (differentieller Querschnitt) (2):
Bsp: Wald
„Fläche auf der die Wirkung Eintritt (z.B. Stoß)“
“Wahrscheinlichkeit”
in einen Winkel zu streuen
Nprojekti
l
Zufällige Verteilung aller
Stoßparameter
http://www.didaktik.physik.uni-erlangen.de/grundl_d_tph/exp_stoss/stoss_streu_3.html
Z1Z2 e2
b=
4o 2mv2 sin2(/2)
d.h.für reine Coulombstreuung an Punktteilchen
erwartet man eine Wahrscheinlichkeitverteilung
der Streuwinkel 1/sin(/2)4
Rutherford/Geiger/Marsden Streuexperiment
Dünne Gold
Folie
Radon Gas
emittiert  Teilchen
Blendenkanal für
gerichteten Strahl
Mikroskop mit
Szintillationsschirm
(drehbar)
Evakuieren damit an Gold, nicht an
Luft gestreut wird
Rutherford/Geiger/Marsden Streuexperiment
Beobachtung:
1) Rückstreuung!
“as if one had fired a large naval shell
at a piece of tissue paper and it had
bounced back”
Widerlegt “plum pudding model”
zeigt lokalisierung von Masse und
Ladung
Rutherford/Geiger/Marsden Streuexperiment
Abweichungen ...
Energie fest,
detektiere Streuwinkel
Setzt reine Coulombstreuung
voraus.
d.h. wenn Kernberührung ->
Abweichungen!
“Coulomb Schwelle”
(einige MeV/u)
Winkel fest, variiere Energie
Setzt reine Coulombstreuung
voraus.
d.h. wenn Kernberührung ->
Abweichungen!
Wirkungsquerschnitt 3:
“allgemeiner” differentieller Wirkunsquerschnitt:
“effektive Fläche”, Fläche pro Messintervall
für das eintreten einer Reaktion:
z.B. Photoabsorbtionsqueschnitt
Anregungsquerschnitt für einen bestimmten Übergang
Erzeugung eines Teilchens
Emission von 10 Teilchen in 10 verschiedene Richtungen und
mit verschiedenen Energien
99eV h + He  He2+ + 2e-
e2
e1
Ee1=Ee2
Polarization
99eV h + He  He2+ + 2e-
e2
e1
Ee1=Ee2
Einheiten!!
Polarization