4. Isotopie und Massenbestimmung 5. Kernstruktur des Atoms
Werbung

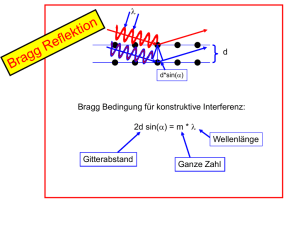
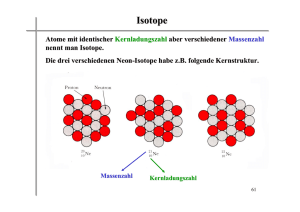
. 1: Einleitung: Atomphysik und Quantenmechanik haben a) weitreichende Implikationen für unser Weltbild b) Immense technische Bedeutung 2. Historischer Rückblick 2.1 Atomtheorie seit den Griechen 2.2. Die Avogadro Konstante (das MOL) Genaue Bestimmung von NA aus Kristallen Bragg Reflexion/ Braggsches Drehwinkel Verfahren Laue Verfahren Debye Scherer Verfahren Nachtrag: Anthracen Details der Streuung hängen nicht nur von den Kernen sondern von der Elektronendichteverteilung ab! Elektronendichteverteilung in Anthracen (Röntgenbeugung) 3: Kann man Atome sehen???? 3.1: Wie gross sind Atome 3.1.1. Bestimmung aus dem Kovolumen: 3.1.2. Röntgenbeugung an Kristallen 3.1.3. Über Gasstreuung: Wirkungsquerschnitt 3.1.3. Was ist ein Wirkungsquerschnitt (totaler Querschnitt) (1): Bsp: Wald „Fläche auf der die Wirkung Eintritt (z.B. Stoß)“ Gesucht! Wirkungsquerschnitt: = (A+B)2 Bei Teilchen kein „Kontakt“ sondern Reichweite der Kraft und Wahrscheinlichkeit! (Bsp. TORWART: a) Reichweite, b)Wahrscheinlichkeit) Nprojekti Nreaktion = Nprojektil Ftarget l „Flächendichte“ (Teilchen/cm2)“ des Targets http://www.didaktik.physik.uni-erlangen.de/grundl_d_tph/exp_stoss/stoss_streu_3.html Voraussetzung: Target so dünn, daß Teilchen nicht überlappen! Allgemein: Nprojekti l Nrest x L Nrest = Nprojektil (1 – e-FL) Messe Wirkungsquerschnitt über Abschwächung des Strahls Od. Mittlere Freie Weglänge im Gas Verschiedene Verfahren liefern unterschiedliches Ergebnis! -> Bild von Atom als Kugel der Radius man so bestimmt ist grobe Näherung Bsp: Atomradius aus Kovolumen Neon 1.2 Argon 1.48 Aus Gitterkonstante 1.6 A (10-10m) 1.9A 3: Kann man Atome sehen???? 3.1: Wie gross sind Atome 3.1.1. Bestimmung aus dem Kovolumen: 3.1.2. Röntgenbeugung an Kristallen 3.1.3. Über Gasstreuung: Wirkungsquerschnitt 3.2 Licht von (einzelnen) Atomen (Falle) Kann man Atome sehen? Kann man mit einzelnen Atomen experimentieren??? 3.2. Licht von einzelnen Atomen Stimulierte Lichtemission von Ionen in Paulfalle (W. Paul Nobelpreis 1989) Das Ion „Astrid“ Stimulierte Lichtemission von Ionen in Paulfalle (W. Paul Nobelpreis 1989) Paulfalle wird Montag behandelt Cs+ Ionen in Paulfalle (Arbeitgruppe Werth, Mainz) 3.3 Spuren von Atomen/Ionen in Nebelkammern Teilchen (Heliumkerne) Stoß Mit Magnetfeld www.nobel.se http://www.unibas.ch/physikdidaktik/TEILCHEN_97/EXPTEST.HTML 3: Kann man Atome sehen???? 3.1: Wie gross sind Atome 3.1.1. Bestimmung aus dem Kovolumen: 3.1.2. Röntgenbeugung an Kristallen 3.1.3. Über Gasstreuung: Wirkungsquerschnitt 3.2 Licht von (einzelnen) Atomen (Falle) 3.3 Spuren von Atomen (Nebelkammer) 3.4 Abtasten (Rastertunnelmikroskop) 3.4. Atome sehen durch Abtasten: Das Rastertunnelmikroskop: Heinrich Rohrer und Gerd Binnig, Nobelpreis 1986 Until the age of 31, I lived partly in Frankfurt and partly in Offenbach, a nearby city. ... While studying physics, I started to wonder whether I had really made the right choice. Especially theoretical physics seemed so technical, so relatively unphilosophical and unimaginative. ... My education in physics gained some significance when I began my diploma work in Prof. Dr. W. Martienssen's group, under Dr. E. Hoenig's guidance. I realized that actually doing physics is much more enjoyable than just learning it.... I have always been a great admirer of Prof. Martienssen, especially of his ability to grasp and state the essence of the scientific context of a problem. ... aus Gerd Binnig Autobiographie http://www.nobel.se/physics/laureates/1986/binnig-autobio.html http://de.geocities.com/rastertunnelmikroskop2002/deutsch •Verschiebung mit Piezos 3 Dimensional •Dämpfung!!! •Messung des Tunnelstroms (wird konstant gehalten durch Höhenvariation) Fehlstelle Siliziumoberfläche STM Aufnahme Atome nicht nur sehen, sondern einzeln manipulieren: Einzelne Xenon Atome, bei –273K (IBM 1989) C60 Moleküle als „Rechenschieber“ (1996) 3: Kann man Atome sehen???? 3.1: Wie gross sind Atome 3.1.1. Bestimmung aus dem Kovolumen: 3.1.2. Röntgenbeugung an Kristallen 3.1.3. Über Gasstreuung: Wirkungsquerschnitt 3.2 Licht von (einzelnen) Atomen (Falle) 3.3 Spuren von Atomen (Nebelkammer) 3.4 Abtasten (Rastertunnelmikroskop) 4. Isotopie und Massenbestimmung 4: Isotopie und Massenbestimmung Periodensystem (1869 Mendelejew, Lothar Meyer) Sortiert nach periodisch wiederkehrenden chemischen&physikalischen Eigenschaften Hassium (von Hessen!) Bei GSI entdeckt Seltene Erden Actinide Ionisationsenergie Edelgase: He, Ne, Ar, Kr, Xe Ordnungszahl Quelle: http://www.monroecc.edu/wusers/flanzafame/PeriodicFigs.htm 4: Isotopie und Massenbestimmung Nichtganzahlige Massen: mittelwert der verschiednen Isotope d.h. verschiedener Anzahl von Neutronen Massenspektrometer: 1) Erzeuge geladene Teilchen: z.B. Elektronenstoßionisation (beschleunige Elektronen die Ionisieren, erzeugt Plasma, siehe Leuchtstoffröhre) Laserfeld: Feldionisation 2) Analysiere q/m durch elektrische Felder magnetische Felder Flugzeit zeitabhängige Felder Lorentzkraft: F = q * (v x B) Elektrisch: F=q*E !geschwindigkeitsabhängig Massenspektrometer: Geladene Teilchen (Ionen) in elektrischen, magnetischen Feldern Lorentzkraft: F = q * (v x B) Elektrisch: F=q*E !Geschwindigkeitsabhängig Kraft senkrecht auf Bewegungsrichtung -> Kreisbahn radius = m/q * v / B zu bestimmen Massenspektrometer: Geladene Teilchen (Ionen) in elektrischen, magnetischen Feldern Lorentzkraft: F = q * (v x B) Elektrisch: F=q*E !Geschwindigkeitsabhängig Ionenquelle m/q Auflösung durch v begrenzt radius = m/q * v / B Aston 1919 „Geschwindigkeitsfokussierung“ Aston: gekreuzte E und B Felder Ziel: verschiedene Geschwindigkeiten auf gleichen Punkt geschickte Kombination von E und B Ablenkung im B Feld tan() = q B L / mv Ablenkung im E Feld: tan() = q B L / mv2 L verschiedene Startwinkel Richtungsfokussierung “Sektorfeld” Massenspektrometrie: Massenzahl 20! 19.9876 – 29.0628 Massenspektrometrie immernoch aktuell: "for their development of soft desorption ionisation methods for mass spectrometric analyses of biological macromolecules" Ionisiere biologische Moleküle ohne sie zu zerbrechen! Quadrupol Massenspektrometer Wolfgang Paul 1913-1993 Nobelpreis 1989 Wechselfelder Näheres: Montags Ergänzungen 3: Kann man Atome sehen???? 3.1: Wie gross sind Atome 3.1.1. Bestimmung aus dem Kovolumen: 3.1.2. Röntgenbeugung an Kristallen 3.1.3. Über Gasstreuung: Wirkungsquerschnitt 3.2 Licht von (einzelnen) Atomen (Falle) 3.3 Spuren von Atomen (Nebelkammer) 3.4 Abtasten (Rastertunnelmikroskop) 4. Isotopie und Massenbestimmung 5. Kernstruktur des Atoms Rutherfordstreuung differentieller Wirkungsquerschnitt 5: Kernstruktur des Atoms Wie ist Ladung und Masse im Atom verteilt? Positive Ladung und Masse lokalisiert oder delokalisiert? 5: Kernstruktur des Atoms Betrachte die STREUUNG geladener Teilchen “Streuwinkel” “Stoßparameter” b 5: Kernstruktur des Atoms “Streuwinkel” “Stoßparameter” b Z1Z2 e2 b= 4o 2mv2 sin2(/2) für Coulomb Abstoßung zwischen Punktteilchen 5: Kernstruktur des Atoms “Streuwinkel” “Stoßparameter” b Z1Z2 e2 Kann nicht b=“Zielen” d.h. kenne b nicht 2 sin2(/2) ist die4 einzige o 2mv Messgröße “Schrotgewehr” Was ist ein Wirkungsquerschnitt (differentieller Querschnitt) (2): Bsp: Wald „Fläche auf der die Wirkung Eintritt (z.B. Stoß)“ Nreaktion = Nprojektil Ftarget Nprojekti l Zufällige Verteilung aller Stoßparameter „Flächendichte“ (Teilchen/cm2)“ des Targets ist proportional zur Wahrscheinlichkeit daß eine Reaktion Eintritt, wenn man “zufällig” (alle Stoßparameter) bestahlt. http://www.didaktik.physik.uni-erlangen.de/grundl_d_tph/exp_stoss/stoss_streu_3.html Was ist ein Wirkungsquerschnitt (differentieller Querschnitt) (2): “Wahrscheinlichkeit” in einen Winkel zu streuen Nprojekti l Zufällige Verteilung aller Stoßparameter http://www.didaktik.physik.uni-erlangen.de/grundl_d_tph/exp_stoss/stoss_streu_3.html Z1Z2 e2 b= 4o 2mv2 sin2(/2) d.h.für reine Coulombstreuung an Punktteilchen erwartet man eine Wahrscheinlichkeitsverteilung der Streuwinkel 1/sin(/2)4 Rutherford/Geiger/Marsden Streuexperiment Dünne Gold Folie Radon Gas emittiert Teilchen Blendenkanal für gerichteten Strahl Mikroskop mit Szintillationsschirm (drehbar) Evakuieren damit an Gold, nicht an Luft gestreut wird Rutherford/Geiger/Marsden Streuexperiment Energie fest, detektiere Streuwinkel Setzt reine Coulombstreuung voraus. d.h. wenn Kernberührung -> Abweichungen! “Coulomb Schwelle” (einige MeV/u) Winkel fest, variiere Energie Setzt reine Coulombstreuung voraus. d.h. wenn Kernberührung -> Abweichungen! Wirkungsquerschnitt 3: “allgemeiner” differentieller Wirkunsquerschnitt: “effektive Fläche”, Fläche pro Messintervall für das eintreten einer Reaktion: z.B. Photoabsorbtionsqueschnitt Anregungsquerschnitt für einen bestimmten Übergang Erzeugung eines Teilchens Emission von 10 Teilchen in 10 verschiedene Richtungen und mit verschiedenen Energien