Baum

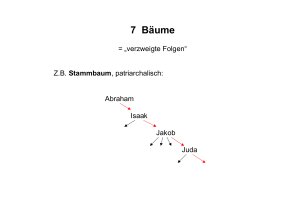
7 Bäume
= „verzweigte Folgen“
Z.B. Stammbaum, patriarchalisch:
Abraham
Isaak
Jakob
Juda
weitere Beispiele für Bäume:
Organisationsbaum
Turnierbaum
Lehrbuchstruktur
Dateibaum
Syntaxbaum
Operatorbaum:
/
a
+
+
b
d
c
e
7.1 Modelle für Bäume
Bäume als spezielle ungerichtete (i.a. endliche) Graphen:
Definition 1: (freier) Baum :
kreisfreier, zusammenhängender Graph (E,K)
mit
E = Menge der Ecken (Knoten, nodes),
K = Menge der Kanten (edges)
(= symmetrische, zweistellige Relation auf E)
Definition 2: (Wurzel-) Baum :
(w,B)
mit freiem Baum B=(E,K) und Wurzel w aus E
(Die Auszeichnung der Wurzel induziert eine Richtung „weg von der Wurzel“)
Rekursive Definitionen:
Definition 3:
Ein geordneter Baum ist eine Folge geordneter Bäume
Wenn die Ordnung ignoriert wird:
Definition 4:
Ein Baum ist eine Multimenge von Bäumen
(Äquivalent zu Definition 2 !)
Invarianten:
Definition 5:
Ein n-ärer Baum (n m 1) ist
entweder
oder
leer
ein k-tupel (k [ n) von n-ären Bäumen
Ein n-ärer Baum mit
n m 3 heißt Vielwegbaum (Mehrwegbaum, multi-way tree)
(in der Regel geordnet)
n=2
heißt Binärbaum (binärer Baum, binary tree)
(in der Regel geordnet)
n=1
ist Liste „ohne Werte“
Terminologie:
Wurzel (root)
(ancestor)
Vater (parent)
Kind (child)
Teilbaum
Unterbaum
Blatt
innerer Knoten
Weg (path) = vertikaler Kantenzug
(descendant)
weiter Terminologie:
Grad (degree) eines Knotens
= Anzahl seiner Kinder
= Anzahl der Teilbäume des zugehörigen Unterbaums,
d.h. desjenigen Baums, dessen Wurzel der Knoten ist
Ebene, Stufe (level) eines Knotens
= Weglänge von der Wurzel bis zum Knoten
Höhe eines Baums
= maximale Ebene/Weglänge
weiter Terminolgie:
Vollständiger Baum:
alle Ebenen sind vollständig besetzt
- eventuell mit Ausnahme der untersten
0
1
2
3
Zur Höhe von Binärbäumen:
n = Knotenanzahl
h = Höhe
N(h) = maximale Knotenanzahl bei Höhe h
B(h) = maximale Blätteranzahl bei Höhe h
(vollständiger Baum)
(vollständiger Baum)
1.
h [ n-1
h = n-1 : zur Kette entarteter Baum
2.
B(h) = 2h
3.
Eine vorgegebene Anzahl n von Knoten kann in einem
vollständigen Baum mit minimaler Höhe h = log2(n+1) - 1
untergebracht werden (weil N(h) m n).
N(h) = 2h+1 - 1
Markierte Bäume
= „verzweigte Folgen“
jeder Knoten k trägt Markierung t(k) mit Basistyp T
Modell 1:
B<T> = { (b,t) | b ist Baum mit Knotenmenge E,
t ist Abbildung E -> T }
Modell 2:
B<S,T> = { (b,s,t) | b ist nichtleerer Baum mit
Knotenmenge E,
s ist Abbildung Blätter -> S,
t ist Abbildung Nichtblätter -> T }
7.2 Spezifikation
... am Beispiel markierter Binärbäume, mit minimaler Signatur:
Modell:
Invariante:
Signatur:
Semantik:
data Tree t = Empty | Node(Tree t) t (Tree t)
-- Empty :: Tree t
-- Node :: Tree t -> t -> Tree t -> Tree t
root :: Tree t -> t
left, right :: Tree t -> Tree t
empty :: Tree t -> Boolean
root (Node l v
left (Node l v
right(Node l v
empty t = t ==
r) = v
r) = l
r) = r
Empty