6 Bäume

6 Bäume
6.1
1
Beispiele für baumartige Strukturen:
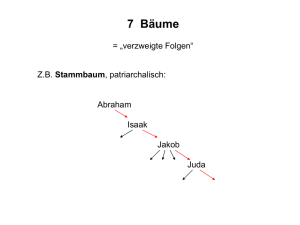
- Stammbaum
- Lehrbuchstruktur
- Hierarchische Organisation
- Repräsentation „höherer“ ADT (Mengen, Relationen, ...) (7)
- Dateibaum
-.....
- Operatorbaum, z.B. für
(a - b + c) * (d - e) :
*
„Wurzel“ oben,
+
keine Operatorvorränge,
keine Klammern !
6.1
a
c
d
e
b
2
6.1 Modelle
Bäume als spezielle ungerichtete Graphen:
Def. 1: (freier) Baum = kreisfreier zusammenhängender Graph
G = (E,K), E = Menge der Ecken/Knoten (nodes),
K ⊆ E × E = Menge der Kanten (edges)
6.1
3
Def. 2: (Wurzel-)Baum = (B,w) mit freiem Baum B und
ausgezeichneter Ecke „Wurzel“ w
Die Auszeichnung der Wurzel induziert eine „Richtung“
von der Wurzel weg, z.B. in der graphischen Darstellung
von oben nach unten:

6.1
4
6.1.1 Rekursive Definitionen
Def. 3: Ein geordneter Baum ist eine Folge geordneter Bäume prägnant formulierbar als algebraischer Typ in Haskell:
data Tree = Node [Tree]
deriving Show
Beispiele: t1 = Node[]
t2 = Node[t1]
t3 = Node[t1,t1]
t7 = Node[t1,t2,t3]
6.1
5
... und wenn man die Ordnung ignoriert:
Def. 4: Ein Baum ist eine Multimenge von Bäumen.
Bei dieser Betrachtung ist t7 mit dem Baum zu Def. 2 identisch!
Def. 5: Ein n-ärer Baum (n≥1) ist
entweder leer
oder ein n-Tupel von n-ären Bäumen
( ≈ geordneter Baum!)
n≥3:
6.1
Vielwegbaum (multi-way tree)
(Bezeichnung auch gebräuchlich für ungeordnete
Bäume nach Def. 4)
6
n=2:
Binärbaum (binary tree), in Haskell:
data Bintree = Empty | Node Bintree Bintree
z.B.
b0 = Empty
b1 = Node Empty Empty
b2 = Node Empty b1
b4 = Node b1 b2
6.1
7
n=1:
Kette = Liste ohne Werte:
data Nontree = Empty | Node Nontree
z.B.
n0 = Empty
n1 = Node Empty
n2 = Node(Node Empty)
n3 = Node n2
. . .
( ! isomorph zu den natürlichen Zahlen:
data Nat = Zero | Succ Nat )
6.1
8
6.1.2 Terminologie
Wurzel (root)
Vater (parent)
Blatt (leaf)
Kind (child)
x
Teilbaum
Unterbaum
6.1
Weg (path) =
vertikaler Kantenzug
9
Grad (degree) eines Knotens = Anzahl der Kinder
(= Anzahl der nichtleeren Teilbäume des zugehörigen Unterbaums)
Ebene, Stufe (level) eines Knotens = Weglänge von der Wurzel
(z.B. 2 beim Knoten x auf S. 9)
Höhe (height) eines nichtleeren Baums = maximale Ebene
(z.B. 3 auf S. 9)
vollständiger n-ärer Baum: alle Ebenen sind vollständig besetzt außer eventuell der untersten - z.B. binär:
0
1
2
6.1
3
10
6.1.3 Zur Höhe von Binärbäumen
n = Knotenanzahl eines Baums, h = Höhe
N(h) = maximal mögliche Knotenanzahl eines Baums der Höhe h
B(h) = maximal mögliche Blätteranzahl eines Baums der Höhe h

h = n-1 ,
falls Baum zur Kette entartet:
... also ist allgemein n ≥ h+1 .
6.1
11

N(h) = 2h+1 - 1 , B(h) = 2h
Bew.:
(Vollständige Induktion)
I. h = 0:
21 - 1 = 1 Knoten 
20
= 1 Blatt

II. Die Behauptung gelte für h:
h+1
h
N(h) = 2h+1 - 1 , B(h) = 2h
Dann ist
6.1
N(h+1) = 2(2h+1 - 1) + 1 = 2h+2 - 1 
B(h+1) = 2•2h = 2h+1 
QED

Wenn eine vorgegebenen Knotenzahl n in einem Baum mit
minimaler Höhe untergebracht werden soll, kann man einen
vollständigen Baum wählen (ein nichtvollständiger Baum
kann jedenfalls keine kleinere Höhe haben).
Die minimale Höhe h ist
 log2 (n+1)  - 1 .
Bew.:
N(h-1) < n ≤ N(h) ,
h
6.1
h-1
vollständig
also
2h - 1 < n ≤ 2h+1 - 1 ,
also
2h < n+1 ≤ 2h+1 ,
also
h < log2 (n+1) ≤ h+1 ,
also
 log2 (n+1)  = h+1 QED
13
6.1.4 Markierte Bäume
Def.:
Markierter Baum (genauer: knotenmarkiert) (labelled tree):
B<T> = { (b,m) | b ist Baum mit Knotenmenge E, m : E  T }
Markierung
Z.B. geordneter (6.1.1, Def. 3) markierter Baum in Haskell:
data Tree t = Node t [Tree t]
Binärbaum:
data Bintree t = Empty | Node(Bintree t) t (Bintree t)
Liste:
data Nontree t = Empty | Node t (Nontree t) isomorph zu
data List t
= Nil
| Cons t (List t)
14
Monomorphe Beispiele:
(Tree)
data Text = Section String [Text]
(Inhaltsverzeichnis eines Lehrbuchs)
(Bintree)
data Person = Unbekannt | Kind String Person Person
(Stammbaum)
z.B.
maria = Kind "Maria"
(Kind "Anna" Unbekannt Unbekannt)
Unbekannt
6.1
jesus = Kind "Jesus"
maria
(Kind "Joseph" Unbekannt Unbekannt)
Variante mit andersartigen Markierungen für die Blätter:
B<S,T> = { (b,s,t) | b ist nichtleerer Baum mit Knotenmenge E,
E = Blätter ∪ Nichtblätter,
s : Blätter  S, t : Nichtblätter  T } ,
z.B. Binärbaum, dessen Knoten den Grad 2 oder 0 (nicht 1!) haben:
data Bintree s t = Leaf s | Node(Bintree s t) t
(Bintree s t)
Monomorphe Spezialisierung:
Operatorbaum:
type Op = Int -> Int -> Int
data Expr = Simple Int | Composite Expr Op Expr
6.1
16
Viele weitere Varianten .....
Übung: Dateibaum mit Haskell modellieren
6.1
17