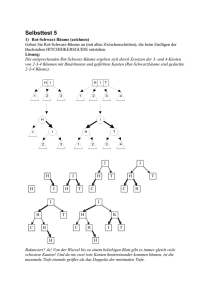
subtree

6.2.1 AVL-Trees
(according to Adelson-Velskii & Landis, 1962)
In normal search trees, the complexity of find, insert
and delete operations in search trees is in the worst
case: (n).
Can be better! Idea: Balanced trees.
Definition: An AVL-tree is a binary search tree such that
for each sub-tree T ' = < L, x, R >
| h(L) - h(R) |  1 holds
(balanced sub-trees is a characteristic of AVL-trees).
The balance factor or height is often annotated at each
node h(.)+1.
1
|Height(I) – hight(D)| < = 1
This is an AVL tree
2
This is NOT an AVL tree (node * does not hold the required condition)
3
Goals
1. How can the AVL-characteristics be kept when
inserting and deleting nodes?
2. We will see that for AVL-trees the complexity of the
operations is in the worst case
= O(height of the AVL-tree)
= O(log n)
4
Preservation of the AVL-characteristics
After inserting and deleting nodes from a tree we must
procure that new tree preserves the characteristics
of an AVL-tree:
Re-balancing.
How ?: simple and double rotations
5
Only 2 cases (an their mirrors)
• Let’s analyze the case of insertion
– The new element is inserted at the right (left) subtree of the right (left) child which was already
higher than the left (right) sub-tree by 1
– The new element is inserted at the left (right) subtree of the right (left) child which was already
higher than the left (right) sub-tree by 1
6
Rotation (for the case when the right sub-tree grows
too high after an insertion)
Is transformed into
7
Double rotation (for the case that the right sub-tree
grows too high after an insertion at its left sub-tree)
Double rotation
Is transformed into
8
b
First rotation
a
c
X
W
a
new
Y
Z
Second rotation
b
W
c
X
Y
Z
9
Re-balancing after insertion:
After an insertion the tree might be still balanced or:
theorem: After an insertion we need only one rotation
of double-rotation at the first node that got
unbalanced * in order to re-establish the balance
properties of the AVL tree.
(* : on the way from the inserted node to the root).
Because: after a rotation or double rotation the
resulting tree will have the original size of the tree!
10
The same applies for deleting
• Only 2 cases (an their mirrors)
– The element is deleted at the right (left) sub-tree of
which was already smaller than the left (right) subtree by 1
– The new element is inserted at the left (right) subtree of the right (left) child which was already
higher that the left (right) sub-tree by 1
11
The cases
Deleted node
1
1
1
12
Re-balancing after deleting:
After deleting a node the tree might be still balanced or:
Theorem: after deleting we can restore the AVL balance
properties of the sub-tree having as root the first* node that
got unbalanced with just only one simple rotation or a double
rotation.
(* : on the way from the deleted note to the root).
However: the height of the resulting sub-tree might be
shortened by 1, this means more rotations might be
(recursively) necessary at the parent nodes, which can affect
up to the root of the entire tree.
13
About Implementation



While searching for unbalanced sub-tree after an operation
it is only necessary to check the parent´s sub-tree only
when the son´s sub-tree has changed it height.
In order make the checking for unbalanced sub-trees more
efficient, it is recommended to put some more information
on the nodes, for example: the height of the sub-tree or
the balance factor (height(left sub-tree) – height(right subtree)) This information must be updated after each
operation
It is necessary to have an operation that returns the parent
of a certain node (for example, by adding a pointer to the
parent).
14
Complexity analysis– worst case
Be h the height of the AVL-tree.
Searching: as in the normal binary search tree O(h).
Insert: the insertion is the same as the binary search tree (O(h))
but we must add the cost of one simple or double rotation,
which is constant : also O(h).
delete: delete as in the binary search tree(O(h)) but we must add
the cost of (possibly) one rotation at each node on the way
from the deleted node to the root, which is at most the height
of the tree: O(h).
All operations are O(h).
15
Calculating the height of an AVL tree
Be N(h) the minimal number of nodes
In an AVL-tree having height h.
Principle of construction
0
N(0)=1, N(1)=2,
N(h) = 1 + N(h-1) + N(h-2) für h  2.
N(3)=4, N(4)=7
remember: Fibonacci-numbers
fibo(0)=0, fibo(1)=1,
fibo(n) = fibo(n-1) + fibo(n-2)
fib(3)=1, fib(4)=2, fib(5)=3, fib(6)=5, fib(7)=8
By calculating we can state:
N(h) = fibo(h+3) - 1
1
2 3
16
Be n the number of nodes of an AVL-tree of height h. Then it
holds that:
n  N(h) ,
By making p = (1 + sqrt(5))/2 und q = (1- sqrt(5))/2
we can now write
n  fibo(h+3)-1
= ( ph+3 – qh+3 ) / sqrt(5) – 1
 ( p h+3/sqrt(5)) – 3/2,
thus
h+3+logp(1/sqrt(5))  logp(n+3/2),
thus there is a constant c with
h  logp(n) + c
= logp(2) • log2(n) + c
= 1.44… • log2(n) + c = O(log n).
17
6.3.1 Heapsort
Idea: two phases:
1. Construction of the heap
2. Output of the heap
For ordering number in an ascending sequence: use a
Heap with reverse order: the maximum number
should be at the root (not the minimum).
Heapsort is an in-situ-Procedure
18
Remembering Heaps: change the definition
Heap with reverse order:
• For each node x and each successor y of x the
following holds: m(x)  m(y),
• left-complete, which means the levels are filled
starting from the root and each level from left to
right,
• Implementation in an array, where the nodes are set
in this order (from left to right) .
19
7.1 Externes Suchen
• Bisherige Algorithmen: geeignet, wenn alle Daten im
Hauptspeicher.
• Große Datenmengen: oft auf externen
Speichermedien, z.B. Festplatte.
Zugriff: immer gleich auf einen ganzen Block (eine
Seite) von Daten, z.B: 4096 Bytes.
Effizienz: Zahl der Seitenzugriffe klein halten!
20
Für externes Suchen: Variante von Suchbäumen mit:
Knoten = Seite
Vielwegsuchbäume!
21
Definition (Vielweg-Suchbaum)
Der leere Baum ist ein Vielweg-Suchbaum mit der Schlüsselmenge
{}.
Seien T0, ..., Tn Vielweg-Suchbäume mit Schlüsseln aus einer
gemeinsamen Schlüsselmenge S, und sei k1,...,kn eine Folge von
Schlüsseln mit k1 < ...< kn. Dann ist die Folge
T0 k1 T1 k2 T2 k3 .... kn Tn
ein Vielweg-Suchbaum genau dann, wenn:
• für alle Schlüssel x aus T0 gilt: x < k1
• für i=1,...,n-1, für alle Schlüssel x in Ti gilt: ki < x < ki+1,
• für alle Schlüssel x aus Tn gilt: kn < x .
22
B-Baum
Definition 7.1.2
Ein B-Baum der Ordnung m ist ein Vielweg-Suchbaum mit
folgenden Eigenschaften
• 1  #(Schlüssel in Wurzel)  2m
und
m  #(Schlüssel in Knoten)  2m
für alle anderen Knoten.
• Alle Pfade von der Wurzel zu einem Blatt sind gleichlang.
• Jeder innere Knoten mit s Schlüsseln hat genau s+1 Söhne.
23
Beispiel: Ein B-Baum der Ordnung 2:
24
Abschätzungen zu B-Bäumen
Ein minimal gefüllter B-Baum der Ordnung m und Höhe h:
• Knotenzahl im linken wie im rechten Teilbaum
1 + (m+1) + (m+1)2 + .... + (m+1)h-1
= ( (m+1)h – 1) / m.
Die Wurzel hat einen Schlüssel, alle anderen Knoten haben m
Schlüssel.
Insgesamt: Schlüsselzahl n in einem B-Baum der Höhe h:
n  2 (m+1)h – 1
Also gilt für jeden B-Baum der Höhe h mit n Schlüsseln:
h  logm+1 ((n+1)/2) .
25
Beispiel
Also gilt für jeden B-Baum der Höhe h mit n Schlüsseln:
h  logm+1 ((n+1)/2).
Beispiel: Bei
• Seitengröße: 1 KByte und
• jeder Eintrag nebst Zeiger: 8 Byte,
kann m=63 gewählt werden, und bei
• einer Datenmenge von n= 1000 000
folgt
h  log 64 500 000.5 < 4 und damit hmax = 3.
26
7.1 Externes Suchen
Definition 7.1.2
Ein B-Baum der Ordnung m ist ein Vielweg-Suchbaum mit
folgenden Eigenschaften
• 1  #(Schlüssel in Wurzel)  2m
und
m  #(Schlüssel in Knoten)  2m
für alle anderen Knoten.
• Alle Pfade von der Wurzel zu einem Blatt sind gleichlang.
• Jeder innere Knoten mit s Schlüsseln hat genau s+1 Söhne.
27
Beispiel: Ein B-Baum der Ordnung 2:
28
Abschätzungen zu B-Bäumen
Ein minimal gefüllter B-Baum der Ordnung m und Höhe h:
• Knotenzahl im linken wie im rechten Teilbaum
1 + (m+1) + (m+1)2 + .... + (m+1)h-1
= ( (m+1)h – 1) / m.
Die Wurzel hat einen Schlüssel, alle anderen Knoten haben m
Schlüssel.
Insgesamt: Schlüsselzahl n in einem B-Baum der Höhe h:
n  2 (m+1)h – 1
Also gilt für jeden B-Baum der Höhe h mit n Schlüsseln:
h  logm+1 ((n+1)/2) .
29
Beispiel
Also gilt für jeden B-Baum der Höhe h mit n Schlüsseln:
h  logm+1 ((n+1)/2).
Beispiel: Bei
• Seitengröße: 1 KByte und
• jeder Eintrag nebst Zeiger: 8 Byte,
kann m=63 gewählt werden, und bei
• einer Datenmenge von n= 1000 000
folgt
h  log 64 500 000.5 < 4 und damit hmax = 3.
30
Algorithmen zum Einfügen und Löschen
von Schlüsseln in B-Bäumen
Algorithmus insert (root, x)
//füge Schlüssel x in den Baum mit Wurzelknoten root ein
suche nach x im Baum mit Wurzel root;
wenn x nicht gefunden
{ sei p Blatt, an dem die Suche endete;
füge x an der richtigen Position ein;
wenn p nun 2m+1 Schlüssel
{overflow(p)}
}
31
Algorithmus Split (1)
Algorithmus overflow (p) =
split (p)
Algorithmus split (p)
Erster Fall: p hat einen Vater
q.
Zerlege den übervollen
Knoten. Der mittlere
Schlüssel wandert in den
Vater.
Anmerkung: das Splitting muss
evtl. bis zur Wurzel
wiederholt werden.
32
Algorithmus Split (2)
Algorithmus split (p)
Zweiter Fall: p ist die
Wurzel.
Zerlege den übervollen
Knoten. Eröffne eine
neue Ebene nach
oben mit einer
neuen Wurzel mit
dem mittleren
Schlüssel.
33
Algorithmus delete (root ,x)
//entferne Schlüssel x aus dem Baum mit Wurzel root
suche nach x im Baum mit Wurzel root;
wenn x gefunden
{ wenn x in einem inneren Knoten liegt
{ vertausche x mit dem nächstgrößeren
Schlüssel x' im Baum
// wenn x in einem inneren Knoten liegt, gibt
// es einen nächstgrößeren Schlüssel
// im Baum, und dieser liegt in einem Blatt
}
sei p das Blatt, das x enthält;
lösche x aus p;
wenn p nicht die wurzel ist
{ wenn p m-1 Schlüssel hat
{underflow (p)} } }
34
Algorithmus underflow (p)
// behandle die Unterläufe des Knoten p
wenn p einen Nachbarknoten hat mit s>m Knoten
{ balance (p,p') }
anderenfalls
// da p nicht die Wurzel sein kann, muss p Nachbarn mit m
Schlüsseln haben
{ sei p' Nachbar mit m Schlüsseln; merge (p,p')}
35
Algorithmus balance (p, p')
// balanciere Knoten p mit seinem Nachbarknoten p'
(s > m , r = (m+s)/2 -m )
36
Algorithmus merge (p,p')
// verschmelze Knoten p mit seinem Nachbarknoten
Führe die folgende Operation durch:
Anschließend:
wenn ( q <> Wurzel)
und (q hat m-1
Schlüssel)
underflow (q)
anderenfalls (wenn (q=
Wurzel) und (q
leer)) {gib q frei und
lasse root auf p^
zeigen}
37
Rekursion
Wenn es bei underflow zu merge kommt, muss
evtl. underflow eine Ebene höher wiederholt
werden.
Dies kann sich bis zur Wurzel fortsetzen.
38
Beispiel:
B-Baum der
Ordnung 2
39
Aufwand
Sei m die Ordnung des B-Baums,
n die Zahl der Schlüssel.
Aufwand für Suchen, Einfügen, Entfernen:
O(h) = O(logm+1 ((n+1)/2) )
= O(logm+1(n)).
40
Anmerkung:
B-Bäume auch als interne Speicherstruktur zu
gebrauchen:
Besonders: B-Bäume der Ordnung 1
(dann nur 1 oder 2 Schlüssel pro Knoten –
keine aufwändige Suche innerhalb von Knoten).
Aufwand für Suchen, Einfügen, Löschen:
O(log n).
41
Anmerkung: Speicherplatzausnutzung:
über 50%
Grund: die Bedingung:
1/2•k  #(Schlüssel in Knoten)  k
Für Knoten  Wurzel
(k=2m)
42
Noch höhere Speicherplatzausnutzung möglich, z.B.
über 66% mit Bedingung:
2/3•k  #(Schlüssel in Knoten)  k
für alle Knoten mit Ausnahme der Wurzel und ihrer
Kinder.
Erreichbar durch 1) modifiziertes Balancieren auch
beim Einfügen und 2) split erst, wenn zwei Nachbarn
ganz voll.
Nachteil: Häufigere Reorganisation beim Einfügen und
Löschen notwendig.
43