statistik_11_05_05

STATISIK
LV Nr.: 0028
SS 2005
11.Mai 2005
1
Streuungsmaße
•
•
•
•
•
•
•
•
Varianz
Standardabweichung
Variationskoeffizient
Mittlere absolute Abweichung
Spannweite
Quartilsabstand
Schiefe
Wölbung
2
Varianz
• Beobachtungswerte a1,...,an (metrisch
skaliert)
• Streuungsmaß: Arithmetische Mittel der
Abweichungsquadrate der Einzelwerte ai von
ihrem arithmetischen Mittel
• Varianz (Mittlere quadratische Abweichung)
n
1
σ 2   (a i  a) 2
n i 1
3
Varianz
• Bsp. Körpergröße von 5 Personen: 162, 170,
155, 187, 179
• Arithmetisches Mittel = 170,6
• Varianz (Mittlere quadratische Abweichung)
σ² = 1/5 · [(162-170,6)² + … + (179-170,6)² ]
σ² = 131,44
4
Varianz
• Streuungsmaß: quadrierte Summe der
Abweichungen - nicht Summe der
Abweichungen von ai von ihrem arithm.
Mittel,
da gilt:
n
 (a
i 1
i
 a)  0
• Mittlere quadratische Abweichung bezogen
auf einen beliebigen Wert M
1 n
MQ(M)   (a i  M)2
n i 1
5
Varianz
• Verschiebungssatz (Beziehung zw. MQ(M)
und Varianz):
2
2
MQ(M)  σ  (a  M)
• Das bedeutet:
– MQ(M)  Varianz
– MQ(M) = σ² wenn M = arithm. Mittel
– Minimumeigenschaft des arithm. Mittels.
n
n
2
(a

a
)

(a

M)
 i
 i
2
i 1
(M  a)
i 1
6
Varianz
• Rechenvereinfachung:
1 n
1 n 2
2
σ   (ai  a)   a i  a 2
n i 1
n i 1
2
• Liegt eine Häufigkeitsverteilung vor:
k Merkmalswerte x1,...,xk mit abs. Häufigkeiten
hi bzw. rel. Häufigkeiten fi (i=1,...,k)
• Varianz:
n
1
σ 2   (x i  x) 2 h i
n i 1
1 n
σ   (x i  x) 2 f i
n i 1
mit
n
1 n
x   xihi   xifi
n i 1
i 1
2
7
Varianz
• Klassifizierte Daten: Häufigkeitsverteilung
• Varianz näherungsweise berechnen, statt der
Merkmalswerte xi werden die
Klassenmitten xi´ verwendet:
1 n
2
σ   (x i  x) 2 h i
n i 1
mit
n
1 n
x   x i h i   x i f i
n i 1
i 1
n
1
σ 2   (x i  x) 2 f i
n i 1
8
Varianz
• Bei unimodalen Verteilungen, ist die
Varianz, die aus den klassifizierten Daten
berechnet wird, größer als die Varianz, die
aus den Einzelwerten berechnet wird.
• Bei konstanten Klasseneinteilungen (Δx):
Sheppardsche Korrektur:
σ
2
corr
(Δ x)
σ 
12
2
2
σ² ... die aus den klassifizierten Daten
näherungsweise bestimmte Varianz
9
Varianz
• Dimension: Quadrat der Dimension der
einzelnen Beobachtungen
• Eigenschaft: Varianz immer  0
• Ist Varianz = 0, liegt keine Streuung vor,
alle Beobachtungswerte sind gleich und
somit auch gleich dem arithmetischen
Mittel.
10
Standardabweichung
• Standardabweichung = Quadratwurzel der
Varianz
n
1
2
σ  σ2 
(a

a
)

i
n i 1
11
Varianz & Standardabweichung
Eigenschaften:
• Lineare Transformation der Einzelwerte ai:
ai* = α + βai (i=1,...,n)
• Dann: Varianz: σ*² = β²σ²
Standardabweichung: σ* = |β| σ
• Sonderfall: β=1, Transformation ai* = α + ai
σ*² = σ² und σ* = σ
12
Varianz & Standardabweichung
• Eigenschaften:
• Varianz einer Grundgesamtheit, die aus 2
Teilgesamtheiten (n1, n2) besteht:
2
2
2
2
n
σ

n
σ
n
(
a

a
)

n
(
a

a
)
2 2
2
2
σ2  1 1
 1 1
n1  n 2
n1  n 2
mit
n 1a 1  n 2 a 2
a
n1  n 2
13
Standardisierung
• Standardisierung:
– Spezielle lineare Transformation
– Bildet aus Einzelwerten ai standardisierte
Werte zi, indem von jedem ai das arithm. Mittel
μ abgezogen wird und durch die
Standardabweichung dividiert wird.
ai  μ
zi 
σ
• Arithm. Mittel der zi immer 0,
• Varianz der zi immer 1.
14
Variationskoeffizient
• Streuung zweier oder mehrerer Verteilungen
mit sich stark voneinander
unterscheidenden Mittelwerten vergleichen
• Relatives Streuungsmaß (für verhältnisskalierte Merkmale mit ausschließlich
positiven Merkmalswerten), bezieht die
Standardabweichung σ (absolutes
Streuungsmaß) auf das arithm. Mittel μ.
σ
VC 
μ
15
MAD Mittlere absolute Abw.
• Arithmetisches Mittel der absoluten
Abweichungen der einzelnen
Merkmalswerte vom Mittelwert (z.B.
arithm. Mittel oder Median)
1 n
MAD   | a i  M |
n i 1
• Minimumeigenschaft des Medians:
1 n
1 n
| a i  Me |   | a i  M |

n i 1
n i 1
M beliebiger Wert
16
MAD
• Häufigkeitsverteilung der Daten
• MAD bezogen auf Mittelwert μ
1 n
MAD   | x i  μ | h i
n i 1
n
MAD   | x i  μ | f i
i 1
• MAD aus Häufigkeitsverteilung von
klassifizierte Daten:
– Merkmalswerte xi durch Klassenmitten xi´
ersetzen.
17
Spannweite (Range)
• Abstand zw. dem größten und dem kleinsten Wert
• Einzelwerte der Größe nach ordnen: a[1],…,a[n]
R = a[n] - a[1]
• Häufigkeitsverteilung von k
Merkmalsausprägungen:
R = xk - x 1
• Häufigkeitsverteilung von klassifizierten Daten:
R = xko - x1u
• Spannweite ist instabil gegenüber Ausreißern
18
Quartilsabstand
• Quartile Q1, Q2 (=Median), Q3 teilen die
Gesamtheit in 4 gleich große Teile.
• α-Quantil:
a(k) falls n·α keine ganze Zahl (k die auf n·α
folgende ganze Zahl)
ãα= 1/2 (a(k)+a(k+1))
falls n·α ganze Zahl k=n·α
• Quartilsabstand (Interquartile Range) definiert als
Spannweite der 50% mittleren Werte:
QA = Q3 – Q1
• Eigenschaft: stabil gegenüber Ausreißern
19
Deskriptive Analyse: Box-Plot
• Box-Plot
– Box: beinhaltet 50% der Daten (Grenzen: 1.
und 3. Quartil), Darstellung des Medians.
– Whiskers: maximal 1,5-mal die Länge der Box.
– Ausreißer: Werte außerhalb der Whiskers.
• Ausreißer
• Krasse Ausreißer
20
Deskriptive Analyse: Box-Plot
• Box-Plot: grafische Darstellung einer
Beobachtungsreihe (Verteilung und Struktur)
210
110
200
100
190
90
180
80
170
70
160
60
150
50
40
140
N=
37
9
38
GR OEßE
N=
38
GE WICHT
21
Deskriptive Analyse: Box-Plot
• Box-Plot für Vergleich von 2 Messreihen:
210
200
9
190
180
170
28
GROEßE
160
150
140
N=
SEX
20
18
w
m
22
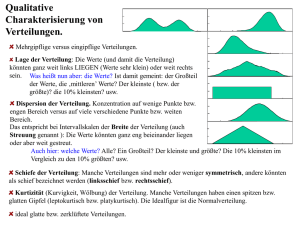
Schiefe
• Gibt Richtung (rechts- oder linksschief) und
Größenordnung der Schiefe einer eingipfligen
Häufigkeitsverteilung an.
1 n

  (ai  a)3 
n i 1


g1 
3
1 n

  (ai  a) 2 
 n i 1

< 0 linksschiefe
g1 = 0 symmetrisch
> 0 rechtsschiefe
• Kein direkter Streuungsparameter
23
Schiefe
• Schiefe einer Häufigkeitsverteilung aus
gruppierten Daten (k Klassen): Verwendung
der Klassenmittel od. der Klassenmitten
1 k

  (a i  a) 3 h i 
n

g1   i 1
3
k
1

  (a i  a) 2 h i 
 n i 1

1 k

  (mi  a) 3 h i 
n

g1   i 1
3
k
1

  (mi  a) 2 h i 
 n i 1

• Berechnung mit Klassenmittel und
Klassenmitte kann zu unterschiedlichen
Ergebnissen führen.
24
Schiefe
• Linksschiefe Verteilung: g1 < 0
Häufigkeit
Linksschiefe Verteilung
Ausprägung
25
Schiefe
• Symmetrische Verteilung: g1 = 0
Häufigkeit
Symmetrische Verteilung
Ausprägung
26
Schiefe
• Rechtschiefe Verteilung: g1 > 0
Häufigkeit
Rechtsschiefe Verteilung
Ausprägung
27
Wölbung
• Wölbung od. Kurtosis od. Exzeß: Maßzahl
für eingipflige Häufigkeitsvt.
• Gibt an, ob (bei gleicher Varianz) das
absolute Maximum der Häufigkeitsvt.
größer als bei der Dichte der Normalvt. ist.
g2 
1 n
(ai  a) 4

n i 1
1
2
  (ai  a) 
 n i 1

n
2
3
28
Wölbung
< 0 abs. Max. kleiner als bei N-Vt.
g2 = 0 Normalverteilung
> 0 abs. Max. größer als bei N-Vt.
• Wölbung einer Häufigkeitsverteilung aus
gruppierten Daten (k Klassen): Verwendung
der Klassenmittel od. der Klassenmitten
k
g2 
1
(a i  a) 4 h i

n i 1
1 n

  (a i  a) 2 h i 
 n i 1

2
3
g2 
1 k
4
(m

a
)
 i hi
n i 1
1

2
(m

a
)
h
  i
i
n
 i 1

n
2
3
29
Konzentrationsmaße
• Metrisch skaliertes Merkmal X mit nur
positiven Ausprägungen
• Frage: Wie teilt sich die Summe der
Merkmalswerte x1,…,xn in der
Beobachtungsreihe auf die Untersuchungseinheiten auf?
• Bsp: n landwirtschaftliche Betriebe, Größe
der Nutzflächen: x1,...,xn. Wie teilt sich die
gesamte Nutzfläche auf die einzelnen
Betriebe auf?
30
Konzentrationsmaße
• n Merkmalswerte werden durch q
Merkmalsausprägungen a1<...<aq mit
absoluten- und relativen Häufigkeiten hi
bzw. fi bestimmt.
• Gesamtbetrag der Merkmalswerte in der
Beobachtungsreihe:
n
n
 x  a h
j1
j
i 1
i
i
31
Konzentrationsmaße
• Lorenzkurve: Grafische Darstellung der
Konzentration der Merkmalswerte
• Koordinatenkreuz:
– Abszisse: es werden die nach der Größe der Merkmalsausprägung geordneten relativen Häufigkeiten
i h
i
aufsummiert
j
ki    f j
für i  1,...,q
j1 n
j1
– Ordinate: Ausprägungen werden der Größe nach
aufsummiert und auf Summe aller Ausprägungen
q
i
bezogen
li   a jh j  a jh j
für i  1,...,q
j1
j1
32
Konzentrationsmaße
• Verbinden der Punkte (ki,li) ergibt die
Lorenzkurve, wobei immer k0=l0=0 und
kq=lq=1 gilt.
1
li
0
ki
1
33
Konzentrationsmaße
• Interpretation: ein Punkt (ki,li) der Lorenzkurve gibt an, dass auf ki · 100% der
Untersuchungseinheiten li · 100% des
Gesamtbetrages aller Merkmalsausprägungen entfallen.
• Bsp. auf ki · 100% der landwirtschaftlichen
Betriebe entfallen li · 100% der gesamten
Nutzfläche
34
Konzentrationsmaße
• Bsp. landwirtschaftliche Betriebe
– Abszisse: Es wird der Prozentsatz der Betriebe
mit der kleinsten Fläche bestimmt, dann wird
der Prozentsatz der Betriebe mit der zweitkleinsten Fläche bestimmt und zum Prozentsatz
der Betriebe mit der kleinsten Fläche addiert,
usw.
– Ordinate: Flächenanteile der Betriebe bzgl. der
Gesamtfläche werden der Flächengröße nach
aufsummiert.
35
Konzentrationsmaße
• Bsp. landwirtschaftliche Betriebe
Flächengröße
bis 5 ha
5 - 10 ha
10 - 20 ha
20 - 50 ha
> 50 ha
Gesamt
Anzahl Flächeng. % der
der
pro
Betriebe
Betriebe Gruppe
21
63
0,42
9
72
0,18
9
135
0,18
8
280
0,16
3
450
0,06
50
1000
1
Flächen- aufsumm. aufsumm.
anteile Betriebs- Flächenanteile
anteile
0,063
0,42
0,063
0,072
0,60
0,135
0,135
0,78
0,270
0,28
0,94
0,550
0,45
1,00
1,000
1
36
Konzentrationsmaße
• Bsp: landwirtschaftliche Betriebe
Landwirtschaftliche Betriebe
1
0,9
aufsummierte Flächenanteile
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
aufsummierte Anteile der Betriebe
0,8
0,9
1
37
Konzentrationsmaße
• Bsp. Landwirtschaftliche Betriebe:
• Interpretation: auf ki · 100% der
landwirtschaftlichen Betriebe entfallen li · 100%
der gesamten Nutzfläche
–
–
–
–
auf 42% der Betriebe entfallen 6,3% der Nutzfläche,
auf 60% der Betriebe entfallen 12,5% der Nutzfläche,
auf 78% der Betriebe entfallen 27% der Nutzfläche,
auf 94% der Betriebe entfallen 55% der Nutzfläche.
38
Konzentrationsmaße
Extremfälle:
• Keine Konzentration, alle Untersuchungseinheiten haben den gleichen Anteil am
Gesamtbetrag. Lorenzkurve ist Diagonale.
• Gesamtbetrag konzentriert sich (fast)
vollständig auf eine Untersuchungseinheit.
Lorenzkurve liegt (fast) auf Abszisse, ist
also (fast) senkrecht.
39
Konzentrationsmaße
Extremfälle:
1
1
0,9
0,9
0,8
0,8
0,7
0,7
0,6
0,6
0,5
0,5
0,4
0,4
0,3
0,3
0,2
0,2
0,1
0,1
0
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0
0,2
0,4
0,6
0,8
1
40
Konzentrationsmaße
• Gini-Koeffizient od. Lorenzsche
Konzentrationsmaß (LKM): Maßzahl für
die Konzentration.
• Definiert als das 2-fache der Fläche F zw.
Diagonale und Lorenzkurve.
LKM = 2F.
• Es gilt immer: 0  LKM  (n-1)/n
• Standardisierter Gini-Koeffizient:
LKMnor = n/(n-1) LKM
41
Konzentrationsmaße
• Berechnung von F:
q
F   Fi  0,5
i 1
k i 1  k i
k i-1  k i
Fi 
(li  li 1 ) 
2
2
a i Hi
q
a H
j1
j
j
– k … Werte auf Abszisse
– l … Werte auf Ordinate
– q … Anzahl der verschiedenen Merkmalsausprägungen
42
Konzentrationsmaße
• Bsp. Landwirtschaftliche Nutzfläche
Flächengröße
bis 5 ha
5 - 10 ha
10 - 20 ha
20 - 50 ha
> 50 ha
Gesamt
Flächenanteile
0,063
0,072
0,135
0,28
0,45
1
aufsumm.
Betriebsanteile
0,42
0,60
0,78
0,94
1,00
2 Fi
0,02646
0,07344
0,18630
0,48630
0,87300
1,6455
• LMK = 2F = i2Fi – 1 = 1,6048 – 1 = 0,6408
– mit i = 1,…,5
• LKMnor = 50/49 · 0,6408 = 0,6539
43
Verhältniszahlen
• Quotient zweier Maßzahlen: Verhältniszahl
• Gliederungszahlen
– Man bezieht eine Teilgröße auf eine ihr
übergeordnete Gesamtgröße
• Beziehungszahlen
– Quotient zweier sachlich sinnvoll in
Verbindung stehender Maßzahlen
• Index-Zahlen
– Quotient zweier Maßzahlen gleicher Art
44
Gliederungszahlen
• Gliederungszahlen
• Bsp. Tagesproduktion 1500 Teile, davon
300 fehlerhaft.
Dann sind 20% der Tagesproduktion
Ausschuss (300/1500·100).
Ausschussanteil ist eine Gliederungszahl
45
Beziehungszahlen
• Beziehungszahlen:
• Verursachungszahlen:
Bezieht Bewegungsmassen auf die
zugehörigen Bestandsmassen.
• Entsprechungszahlen:
Alle Beziehungszahlen, bei denen man
Ereignisse nicht auf ihren Bestand beziehen
kann.
46
Beziehungszahlen
• Bsp. Verursachungszahlen: Geburtenziffer
Bestandsmasse: Einwohner einer Stadt (E)
Bewegungsmasse: Zahl der Lebendgeborenen (L)
G = (L/E)*1000
Sagt, wie viele Geburten auf 1000
Einwohner einer Stadt entfallen.
47
Beziehungszahlen
• Bsp. Entsprechungszahlen:
Schüler-Lehrer-Verhältnis
(Zahl der Schüler) / (Zahl der Lehrer)
Sagt, wie viele Schüler (ungefähr) auf eine
Lehrer entfallen. Dies entspricht aber i.A.
nicht der durchschnittlichen Klassengröße.
48
Indexzahlen
• Indexzahlen: Es werden zwei Maßzahlen
der gleichen Art in Beziehung gesetzt.
• Messzahlen oder Einfache Indizes
– Die zugehörigen Maßzahlen beschreiben eine
realen Sachverhalt.
• (Zusammengesetzte) Indexzahlen
– Eine der Maßzahlen ist eine Zahl, die einen
fiktiven Zustand beschreibt.
49
Indexzahlen
• Einfache Indizes:
• Reihe von Maßzahlen, die man in
Beziehung zueinander setzen will.
x0,...,xt Maßzahlen zu Zeitpunkten t, x0
Maßzahl zum Basiszeitpunkt 0.
Dann ist
I0t = xt / x0
für t = 0, 1, 2, ...
eine Zeitreihe einfacher Indizes
50
Indexzahlen
• Messzahlen werden oftmals mit 100 multipliziert.
• Bsp. Umsatz im Jahr 5, bezogen auf Jahr 0:
I05·100 = x5/x0 · 100 = 87
D.h. dass 87% des Umsatzes im Basisjahr im Jahr
5 umgesetzt werden.
Oder: Es liegt eine Minderung des Umsatzes um
13% vor.
• Vergleich von I05·100=87 mit I06·100=90:
Der Umsatz ist um 3 Prozentpunkte gestiegen.
51
Indexzahlen
• Umbasieren:
Gegeben: Indizes I0t zur Basisperiode 0
Gesucht: Indizes Ikt zur Basisperiode k
Berechung ohne Ursprungsdaten:
xt
x t x 0 I 0t
I kt 


x k x k x 0 I 0k
• Verkettung: Wenn für xt I0t berechnet
werden soll, und x0 nicht bekannt ist.
I0t = I0k · Ikt
52
Indexzahlen
• Bsp. Umsatz für Jahre 1990 bis 1998
Jahr
1990
1991
1992
1993
1994
1995
1996
1997
1998
Umsatz
1240
1210
1180
1190
1150
1080
1120
1130
1200
xt / x0
1,00
0,98
0,95
0,96
0,93
0,87
0,90
0,91
0,97
xt / x4
1,08
1,05
1,03
1,03
1,00
0,94
0,97
0,98
1,04
53
Indexzahlen
• Umbasieren: Index von 1996 zur
Basisperiode 1990 sollen in Index zur
Basisperiode 1994 umgerechnet werden.
– I1990,1996 = 0,90 (Basisperiode 1990)
– I1990,1994 = 0,93 (Basisperiode 1990)
– I1994,1996 = 0,90 / 0,93 = 0,97 (Basisperiode 1994)
• Verkettung: Weiterer Wert für 1998
– I1990,1998 = I1990,1994 · I1994,1998 = 0,93 · 1,04 = 0,97
54
Indexzahlen
• Zusammengesetzte Indexzahlen (Indizes):
• Betrachte Warenkorb:
n Waren zu einem Zeitpunkt t
Mengen qt1,...,qtn
Preise pt1,...,ptn
Wert des Warenkorbes in Periode t:
n
p
i 1
ti
q ti
55
Indexzahlen
• Wertindex:
Vergleich Wert eines Warenkorbes zur
Berichtsperiode t mit dem zur Basisperiode 0
n
W0t 
p
i 1
n
p
i 1
ti
q ti
0i
q 0i
56
Indexzahlen
• Bsp. Durchschnittlicher Verbrauch an Fleisch
aller privaten Haushalte in einer Gemeinde.
Basismonat 1, Berichtsmonat 12.
– (Mengen in g, Preise in DM/kg)
Fleisch
F1
F2
F3
F4
F5
F6
F7
gesamt
p0i
5,75
12,25
24,1
17,8
4,55
10,25
8,9
q0i
1450
1260
50
210
2450
1310
980
7710
p12i
6,2
13,55
24,8
18,1
4,6
10,4
9,1
q12i
1410
1200
50
215
2470
1230
930
7505
57
Indexzahlen
• Bsp. Wertindex
n
7
W0t 
p q
i 1
n
p
i 1
Fleisch
F1
F2
F3
F4
F5
F6
F7
gesamt
ti
ti
0i
q 0i
p0i
5,75
12,25
24,1
17,8
4,55
10,25
8,9

p
i 1
7
p
q0i
1450
1260
50
210
2450
1310
980
7710
i 1
q
12i 12i
0i
q 0i
p12i
6,2
13,55
24,8
18,1
4,6
10,4
9,1
62750,5

 1, 0119
62012,5
q12i
1410
1200
50
215
2470
1230
930
7505
p0q0i
8337,5
15435
1205
3738
11147,5
13427,5
8722
62012,5
p12iq12i
8742
16260
1240
3891,5
11362
12792
8463
62750,5
58
Indexzahlen
• Bsp. Wertindex
– 100 · W012 = 100 · 1,0119 = 101,19
– D.h. der tatsächliche Aufwand für Fleisch für die
privaten Haushalte ist vom Basismonat bis zum
Berichtsmonat um 1,19% gestiegen.
– Es ist hier nicht berücksichtigt, dass der
durchschnittliche Verbrauch im Berichtsmonat
um 205g geringer ist.
59
Indexzahlen
• Preisindizes:
• Aussagen über die Preisentwicklung
• Für verschiedene Perioden das gleiche
Mengenschema verwenden
60
Indexzahlen
• Preisindex nach Paasche
n
P0,Pt 
p
ti
q ti
p
0i
q ti
i 1
n
i 1
• Man vergleicht den Wert eines Warenkorbes
qt1,...,qtn zur jeweiligen Berichtsperiode t mit
dem Wert, den dieser unter der
Preissituation zur Basisperiode gehabt hätte.
61
Indexzahlen
• Bsp. Preisindex nach Paasche
n
P0,Pt 
p
ti
q ti
p
0i
q ti
i 1
n
i 1
Fleisch
F1
F2
F3
F4
F5
F6
F7
gesamt
p0i
5,75
12,25
24,1
17,8
4,55
10,25
8,9
q0i
1450
1260
50
210
2450
1310
980
7710
p12i
6,2
13,55
24,8
18,1
4,6
10,4
9,1
q12i
1410
1200
50
215
2470
1230
930
7505
p0q0i
8337,5
15435
1205
3738
11147,5
13427,5
8722
62012,5
p12iq12i
8742
16260
1240
3891,5
11362
12792
8463
62750,5
p0iq12i
8107,5
14700
1205
3827
11238,5
12607,5
8277
59962,5
p12iq0i
8990
17073
1240
3801
11270
13624
8918
64916
62
Indexzahlen
• Bsp. Preisindex nach Paasche
n
100 P 
P
0, t
p q
i 1
n
p
i 1
7
ti
ti
0i
q ti
 100
p
i 1
7
p
i 1
q
12i 12i
q
62750,5
 100
 104,65
59962,5
0i 12i
• D.h. nimmt man für beide Monaten den
durchschnittlichen Verbrauch an Fleisch im
Berichtsmonat als Mengenschema
(Warenkorb) an, so sind die Preise in
diesem Zeitraum um 4,65% gestiegen.
63
Indexzahlen
• Preisindex nach Laspeyres
n
P0,Lt 
p
ti
q 0i
p
0i
q 0i
i 1
n
i 1
• Der Warenkorb q01,...,q0n der Basisperiode 0
wird für alle Berichtsperioden
zugrundegelegt und ihr fiktiver Wert zur
Berichtsperiode t wird mit seinem Wert zur
Basisperiode verglichen.
64
Indexzahlen
• Bsp. Preisindex nach Laspeyres
n
100 P 
L
0, t
p q
i 1
n
p
i 1
ti 0i
0i
q 0i
7
 100
p
i 1
7
12i
p
i 1
0i
q 0i
q 0i
64916
 100
 104,68
62012,5
• D.h. Für die im Basismonat verbrauchten
Mengen an Fleisch muss man in der
Berichtsperiode 4,68% mehr Geld
ausgeben.
65
Indexzahlen
• Vergleich Preisindizes nach Paasche und
Laspeyres:
• L: Warenkorb muss nur für Basisperiode
bestimmt werden, Kosten (+) Aktualität (-)
• P: Warenkorb muss für Berichtsperioden
bestimmt werden, Kosten (-) Aktualität (+)
• Vergleich. Sind Abweichungen groß, muss
der Warenkorb neu festgelegt werden.
• Fishersche Idealindex: I F  I P  I L
66
Indexzahlen
• Mengenindizes:
• Aussagen über Mengenentwicklung
(unabhängig von der Preisentwicklung)
67
Indexzahlen
• Mengenindex nach Paasche
n
Q 0,P t 
p
ti
q ti
p
ti
q 0i
i 1
n
i 1
• Standardisierung nach den Preisen zur
Berichtsperiode
68
Indexzahlen
• Bsp. Mengenindex nach Paasche
n
100 Q 0,P t 
p q
i 1
n
ti
p q
i 1
7
ti
ti 0i
 100
p
i 1
7
q
12i 12i
p
i 1
12i
q 0i
 100
62750,5
 96,66
64916
• D.h. der Verbrauch an Fleisch, gewichtet
mit den Preisen im Berichtsmonat ist um
3,34% gesunken.
69
Indexzahlen
• Mengenindex nach Laspeyres
n
Q 0,L t 
p
0i
q ti
p
0i
q 0i
i 1
n
i 1
• Standardisierung nach den Preisen zur
Basisperiode
70
Indexzahlen
• Bsp. Mengenindex nach Laspeyres
n
100 Q
L
0, t

p
i 1
n
p
i 1
7
0i
0i
q ti
q 0i
 100
p
i 1
7
p
i 1
q
0i 12i
0i
q 0i
59962,5
 100
 96,69
62012,5
• D.h. der Verbrauch an Fleisch, gewichtet
mit den Preisen zum Basismonat, ist um
3,31% gesunken.
71