Lösungsblatt 02

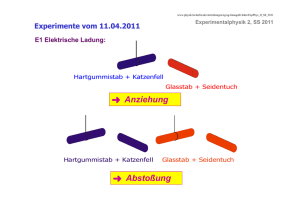
Titel: Lösungen zu Elektrotechnik/Elektronik
URL: ..\Etechnik_1\Aufgaben\a_blatt02.doc
Autor: Prof. Dr. J. Wiebe
1 für I u. M
08.04.17
04:39h
Aufgabe 1
In einem homogenen elektrischen Feld ergibt sich die Verschiebearbeit (~energie) des Feldes aus
We = F  s = Q  E  s . F: Feldkraft, s: Verschiebeweg. Das Vektorprodukt beinhaltet, daß nur der
Weganteil parallel zu den elektrischen Feldlinien zählt.
a)
We = Q E 5mm = 110-9As 2V/mm 5mm = 110-8 VAs
b)
We = - We von a) , weil Q negativ ist. Der Weg (b) ist
zwar länger als in (a), es zählt aber nur die Komponente
parallel zum E-Feld.
c)
We = Q (-3mm), der Weganteil verläuft gegen das Feld.
Lösungen:
a) We = 10-8Ws; b) We = - 10-8Ws; c) We = - 6.10-9Ws
Aufgabe 2
Spannung U = E  s . Es zählt nur der Weg parallel zum E-Feld, hier also die kürzeste Verbindung
zwischen den Äquipotentialflächen. Die Ladung kommt in der Gleichung nicht vor, sie spielt keine
Rolle.
Zu a) und b): U = 2V/mm 5mm; Anfangspunkt auf höherem Potential als Endpunkt.
Zu c): U = 2V/mm (-3mm); Anfangspunkt auf tieferem Potential als Endpunkt.
Lösungen: a) und b) U = + 10V; c) U = - 6V
Aufgabe 3
Die positive Punktladung bewirkt durch Influenz (siehe
Vorlesung) eine Ladungstrennung in der Metallhülle: positive
Ladungen am Außenrand, negative am Innenrand. Die
Influenzladungen heben das elektrische Feld in der Metallhülle
auf. Von den positiven Ladungen am Außenrand setzt es sich
genauso fort, als ob die Metallhülle nicht existieren würde.
Der Betrag der Influenzladungen ist jeweils gleich Q.
Aufgabe 4
Der schiefe Feldvektor E wird in eine zur Grenzfläche senkrechte und eine tangentiale Komponente
zerlegt. Die tangentiale Komponente würde Ladungen in der
Metalloberfläche solange verschieben, bis sich infolge
Ladungstrennung und entsprechender Verteilung ein Gegenfeld
eingestellt hat, das die äußere tangentiale Feldstärke kompensiert. Im
statischen Fall ist die tangentiale Komponente verschwunden.