Handout zum Referat „DA\AD-Umsetzung“
Werbung

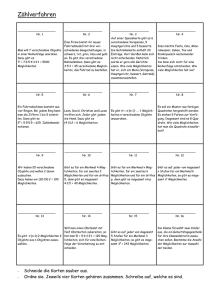
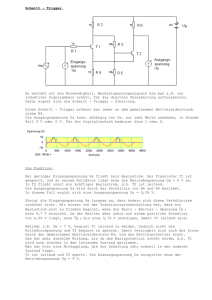
Handout zum Referat „DA\AD-Umsetzung“ 1. Was sind DA\AD-Umsetzer? ADU: Analog-Digital-Umsetzer •wandelt eine angelegte Spannung in eine dazu proportionale Zahl •Überführungsgleichung: Z=Ue/ULSB •ULSB=(Umax – Umin) / 2^n DAU: Digital-Analog-Umsetzer •wandelt eine Zahl in eine dazu proportionale Spannung • Überführungsgleichung: Ua=ULSB*Z 2. Grundprinzipien der DA-Umsetzung a)Parallelverfahren •Spannungsteiler stellen alle möglichen Spannungen bereit •“1 aus n“-Decoder schließt den Schalter, dem die jeweilige Spannung zugeordnet ist und erzeugt damit die gewünschte Ausgangsspannung b)Wägeverfahren •es ist jedem Bit ein Schalter zugeordnet •durch gewichtete Widerstände wird die Ausgangsspannung aufsummiert c)Zählverfahren •ein Schalter wird periodisch geöffnet und geschlossen •sein Tastverhältnis wir durch einen Pulsbreitenmodulator so eingestellt, dass der arithmetische Mittelwert der Ausgangsspannung den gewünschten Wert annimmt 2.1 Vergleich der Verfahren Durch die hohe Anzahl der Schalter wird das Parallelverfahren kaum eingesetzt. Das Zählverfahren gewinnt durch einfach zu integrierende Pulsbreitenmodulatoren an Bedeutung. Das häufigste Verfahren ist das Wägeverfahren. 2.2 Genauigkeit a)Nullpunktfehler •wird durch Sperrströme bestimmt, die durch die geöffneten Schalter fließen b)Vollausschlagfehler •wird durch die Widerstände der Schalter und den Gegenkopplungswiderstand RFB hervorgerufen => a) und b) lassen sich durch Abgleich beheben c)Nichtlinearität •gibt an wieviel eine Stufe im ungünstigsten Fall größer oder kleiner als 1 LSB ist •in der linken Abb. Beträgt die Nichtlinearität +-½ LSB und in der rechten +-1 ½ LSB 3. Grundprinzipien der AD-Umsetzung 3a) Parallelverfahren •Eingangsspannung wird mit „n“ Referenzspannungen verglichen •vollständige Zahl in einem Schritt 3b) Wägeverfahren •jede Stelle der Dualzahl wird nacheinander ermittelt •man beginnt die Vergleiche mit der Referenzspannung an der höchsten Stelle 3c) Zählverfahren •man zählt ab wie oft man die Referenzspannung addieren muss bis man die Eingangsspannung erhält 3.1 Vergleich der Verfahren Technik Zahl der Schritte Zahl d. Referenzspannungen Besondere Merkmale Parallel-verfahren 1 Wäge-verfahren N = ldn Zähl-verfahren n = 2^N n = 2^N N = ldn 1 aufwendig,schnell Einfach, langsam 3.2 Ausführung der Verfahren a)Parallelverfahren •Komperatoren vergleichen die Eingangsspannung mit den jeweiligen Referenzspannungen an den Spannungsteilern •der Prioritätsdecoder übersetzt das Ergebnis in die dazugehörige Dualzahl b)Wägeverfahren •Komparator vergleicht den gespeicherten Messwert mit der Ausgangsspannung des DAUmsetzers •zu Messbeginn wird die Zahl Z auf 0 gesetzt •nun wird das höchste Bit auf 1 gesetzt und nach der Umwandlung durch einen DA-Umsetzer geprüft, ob die Eingangsspannung größer als U(Z) ist •ist dies der Fall bleibt es gesetzt, ansonsten wird es wieder gelöscht •im Register entsteht so nacheinander die gesuchte Zahl (siehe nächste Abb.) c)Zählverfahren •es werden nacheinander die Eingangsspannung und die Referenzspannung des kleinsten Bits, mit inversen Vorzeichen, integriert •dabei wird der Kondensator zunächst aufgeladen und dann wieder entladen •aus den Aufladungs- bzw. Entladungszeiten lässt sich dann die Eingangsspannung bzw. die dazugehörige Zahl berechnen 3.3 Genauigkeit von DA-Umsetzern a) Quantisierungsfehler •bei Umsetzung einer analogen Größe in eine Zahl mit endlich vielen Bits entsteht durch begrenzte Auflösung ein Fehler von +- ½ LSB b) Verstärkungsfehler •ist eine konstante, relative Abweichung vom Anstieg 1 der Übertragungs-Geraden c) Offsetfehler •ist eine konstante, absolute Abweichung, dabei geht die Übertragungs-Geraden nicht durch den Ursprung des Koordinatensystems d) Nichtlinearität (DNL, INL) •es gibt die differentielle (links) und die integrale (rechts) Nichtlinearität • DNL bezeichnet den Unterschied zwischen der schlechtesten binären Schrittweite und dem idealen 1 LSB • INL ist definiert als die Abweichung der Transferfunktion von der idealen Geraden 3.4 Anwendung von AD-Umsetzern •das Zählverfahren wird für kleine Frequenzen verwendet (z.B. in einem Multimeter) •das Wägeverfahren bei mittleren Frequenzen •das Parallelverfahren bei hohen Frequenzen (z.B. in einem Digital-Oszilloskop)