3.2 Materiewellen
Werbung
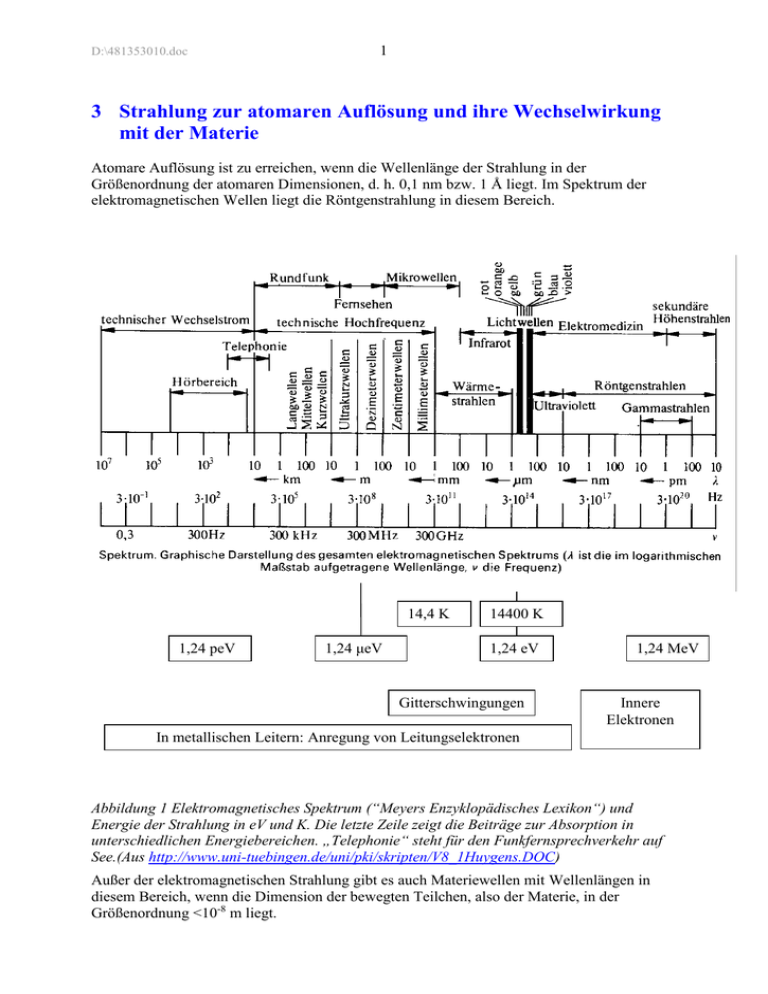
D:\481353010.doc 1 3 Strahlung zur atomaren Auflösung und ihre Wechselwirkung mit der Materie Atomare Auflösung ist zu erreichen, wenn die Wellenlänge der Strahlung in der Größenordnung der atomaren Dimensionen, d. h. 0,1 nm bzw. 1 Å liegt. Im Spektrum der elektromagnetischen Wellen liegt die Röntgenstrahlung in diesem Bereich. 14,4 K 1,24 peV 1,24 μeV 14400 K 1,24 eV Gitterschwingungen 1,24 MeV Innere Elektronen In metallischen Leitern: Anregung von Leitungselektronen Abbildung 1 Elektromagnetisches Spektrum (“Meyers Enzyklopädisches Lexikon“) und Energie der Strahlung in eV und K. Die letzte Zeile zeigt die Beiträge zur Absorption in unterschiedlichen Energiebereichen. „Telephonie“ steht für den Funkfernsprechverkehr auf See.(Aus http://www.uni-tuebingen.de/uni/pki/skripten/V8_1Huygens.DOC) Außer der elektromagnetischen Strahlung gibt es auch Materiewellen mit Wellenlängen in diesem Bereich, wenn die Dimension der bewegten Teilchen, also der Materie, in der Größenordnung <10-8 m liegt. 2 D:\481353010.doc Photonen- und Materiewellen unterscheiden sich vor allem in der Ausbreitungsgeschwindigkeit, die bei Photonen immer gleich der Lichtgeschwindigkeit ist. In Materienwellen dagegen gibt es Dispersion, die Ausbreitungsgeschwindigkeit wächst mit der Wellenzahl. Die de Broglie Beziehung setzt Impuls und Wellenzahl in einen Zusammenhang. Dadurch wird bei elektromagnetischen Wellen den Photonen ein Impuls zugeordnet, und umgekehrt, bei Teilchenwellen, den Teilchen mit mechanischem Impuls eine Wellenzahl. Periodizität in der Zeit Periodizität im Raum Verknüpfung zwischen Periodizität in Raum und Zeit Energie Welle-Teilchen Dualismus: 1 , 2 T 2 k v Ph T E h p h k Frequenz, Kreisfrequenz, Periode T Wellenzahl zur Welle mit Wellenlänge Phasengeschwindigkeit Energie in Abhängigkeit von der Frequenz De Broglie-Beziehung: Dem Impuls entspricht eine Wellenzahl Tabelle 1 Begriffe zu Photonen- und Teilchen-Wellen 3.1 Photonenwellen Für Photonenwellen ist die Phasengeschwindigkeit v Ph immer die Lichtgeschwindigkeit c . Photonen zeigen aber, obwohl ihnen keine Ruhemasse zugeordnet werden kann, außer der Energie E einen Impuls p . Für Photonen (Teilchen ohne Ruhemasse) gilt: v Ph c c T E h p h Die Phasengeschwindigkeit ist immer die Lichtgeschwindigkeit Die Wellenlänge ist proportional zur Periode Energie des Photons Impuls des Photons (De BroglieBeziehung) Tabelle 2 Energie, Impuls für Photonen (elektromagnetische Wellen) 3 D:\481353010.doc Für elektromagnetische Strahlung einer gewünschten Wellenlänge kann aus diesen Beziehungen die Anregungsenergie berechnet werden: c E h Abbildung 2 Berechnung der Anregungsenergie für Photonenstrahlung 1Ǻ=0,1 nm c E h 3 1018 Hz Kürzeste Wellenlänge , die durch ein Elektron nach Durchlaufen der Anregungsspannung U angeregt werden kann ch 1,99 10 15 J = 12415 eV [ Ǻ] ch 12,4 E U kV Tabelle 3 Photonenstrahlung: Frequenz, Energie für 0,1 nm und Berechnung der kürzesten Wellenlänge in Abhängigkeit von der Anregungsenergie 3.2 Materiewellen Zur Deutung der Materiewellen wird die de Broglie Relation gewissermaßen von links nach rechts gelesen: Bewegten Teilchen mit Masse und einem mechanischen Impuls p wird eine Wellenlänge zugeordnet: p mv Für bewegte Teilchen mit endlicher Ruhemasse gilt: E h p2 2m h2 h 2m2 v Ph h 2 m Ein Teilchen mit Masse m und Geschwindigkeit v erscheint als Welle mit Wellenlänge Die Energie der Welle ist gleich der kinetischen Energie des Teilchens Aus E h folgt die Dispersionsrelation für Materiewellen Die Phasengeschwindigkeit ist umgekehrt proportional zur Wellenlänge Tabelle 4 Energie, Impuls , Dispersionsrelation für Materiewellen (Neutronen, Elektronen, Moleküle) 4 D:\481353010.doc Wahrscheinlichkeitsdichte 0,0008 0,0006 0,0004 0,0002 Te mp era tur K 0,0000 100 200 300 Maxwellsche Geschwindigkeitsverteilung für Neutronen 400 500 600 1000 2000 3000 4000 5000 6000 Geschwindigkeit m/s Abbildung 3 Maxwellsche Geschwindigkeitsverteilung eines Gases aus Neutronen (vgl. http://www.uni-tuebingen.de/uni/pki/skripten/V5_4Loesungen.DOC - V_Mittel) Im Gegensatz zur Photonenstrahlung hängt bei Materiewellen die Ausbreitungsgeschwindigkeit von der Wellenlänge ab, man spricht in diesem Fall von Dispersion und nennt die Ausbreitungsgeschwindigkeit zu einer bestimmten Wellenlänge „Phasengeschwindigkeit“. p mv h v Ph E p2 2m E h h 2m Abbildung 4 Berechnung der kinetischen Energie für Teilchenstrahlung und der Phasengeschwindigkeit 5 D:\481353010.doc Art und Masse des Teilchens Geschwindigkeit v E 1 m v2 2 3300 m s 0,05 eV 0,12 nm = 1,2 Ǻ 2200 m s 0,025 eV 0,18 nm = 1,8 Ǻ 1,9 10 8 m/s (schon nahe an c!) 100 keV 0,004 nm = 0,04 Ǻ Neutron 1,672614 (11) 10-27 kg Elektron 9,109558 (54) 10-31 kg De Broglie Wellenlänge h mv Energie Tabelle 5 Geschwindigkeiten und Wellenlängen für thermische Neutronen und nichtrelativistische Elektronen Masse des Elektrons me 9,109558 (54) 10-31 kg Masse des Neutrons mn 1,672614 (11) 10-27 kg v 3300 m s 1 eV 1,6 10 -19 J Plancksche Konstante h 6,626176 10 34 J s Vakuum Lichtgeschwindigkeit c 2,99792458 108 m/s Mittlere Geschwindigkeit der Neutronen bei 300 K aus der Maxwellverteilung Energie-Umrechnung Tabelle 6 Einige Konstanten und Umrechnungsfaktoren für Materiewellen 3.2.1 Die Gruppengeschwindigkeit Weil die Phasengeschwindigkeit für Materiewellen von der Wellenzahl abhängt, verbreitert sich ein im Raum lokalisiertes Wellenpaket während seines Transports im Ortsraum. Ein Paket ist eine Überlagerung aus vielen Wellenzügen zu unterschiedlichen Wellenzahlen, wie man aus der Fourier-Zerlegung erkennt. Jede Komponente zeigt eine andere Ausbreitungsgeschwindigkeit. Um trotzdem die Geschwindigkeit des sich verbreiternden Pakets anzugeben, führt man die Gruppengeschwindigkeit ein, sie zeigt die Geschwindigkeit des Schwerpunkts der Umhüllenden des Pakets. vG v Ph 0 0 dv Ph d 0 Gruppengeschwindigkeit eines Wellenpakets mit mittlerer Wellenlänge 0 und zu dieser Welle gehörender Phasengeschwindigkeit v Ph 0 Tabelle 7 Gruppengeschwindigkeit eines Wellenpakets 6 D:\481353010.doc 3.2.2 Welle- Teilchen-Dualismus, die Unschärferelation Die Verbindung von Welle und Teilchen bringt begrifflich Gegensätzliches zusammen: Der Aufenthaltsort ist eine charakteristische Angabe für ein Teilchen. Die Wellenzahl charakterisiert den Wellenzug. Bei einem Wellenzug ist die Frage nach seinem Ort nicht sinnvoll, denn er ist unendlich ausgedehnt. Wird ein Teilchen durch einen einzigen Wellenzug beschrieben, dann steht die Information über das Teilchen in der Wellenzahl. Nach der de Broglie Relation ist damit der Impuls des Teilchens angegeben. Weil aber am Wellenzug keine Stelle bevorzugt ist, bleibt bei dieser Beschreibung die Frage nach dem Ort des Teilchens unbeantwortet. Impuls und Ort können also nicht zugleich mit beliebiger Genauigkeit angegeben werden. Das ist die Aussage der Heisenbergschen Unschärferelation: x p 2 Tabelle 8 Heisenbergsche Unschärferelation Das Produkt aus Ortsunschärfe x und Impulsunschärfe p in Richtung der Ortskoordinate ist größer als die halbe PlanckKonstante











