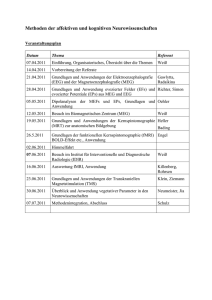
Témaspecifikus szabályok
Werbung

Nagy Judit németről magyarra fordítás , szaknyelv: matemaika 2006. 05.13 Quelle: R. Fischer – G. Malle: Mensch und Mathematik. Eine Einführung in didaktisches Denken und Handeln. Wissenschaftsverlag, 1985. S. 212–218. 2006. március Nagy Judit 1074,Budapest, Huszá u 6 /fsz . 6 06-20-368-52-07 [email protected] További heurisztikus szabályok Pólya kimond néhány heurisztikus szabályt munkájában (mindenekelőtt 1949), amelyek a matematikában általánosan alkalmazhatók, és a tanítás során időnként hasznosak lehetnek. Ezen szabályok közülük néhányat felsorolunk, és példákon keresztül szemléltetjük őket. (1) Vezesd vissza a problémát egy már ismertre! Ismersz hasonló vagy rokon feladatot, amit már megoldottál? Van olyan része a feladatnak, amit már meg tudsz oldani? 04 Ismerjük a háromszög a oldalát, α és β szögét! Számoljuk ki b és c oldalt! Ennél a feladatnál feltételezzük, hogy a tanulók derékszögű háromszögre már igen, de hegyesszögű háromszögre még nem tudják megoldani. A feladat visszavezethető a már ismert példára, ha a háromszöget két derékszögű háromszögre bontjuk fel. (2) Keress összefüggéseket! Ismersz vagy látsz működési, algebrai, logikai vagy más összefüggést? Hogy változik az egyik, ha a másik megváltozik? 05 Vízszintes talajon egy torony előtt található megfigyelési pontból a toronyablak alsó része, amely a talajtól a méter magasan fekszik, α emelkedési szögben, az ablak felső része β emelkedési szögben látszik. Milyen nagy toronyablak? Ha nem látunk semmilyen megoldási menetet, először megpróbálhatunk valamilyen algebrai összefüggést megadni x, a, α és β között. A közvetlen kapcsolat nem nyilvánvaló. Ha még y-t is bevezetjük, akkor felismerhetjük az a = y · tgα és a + x = y · tgβ összefüggéseket. Ezekből adott körülmények között látható, hogy y kiküszöbölése révén megkapjuk a keresett x magasságot. (3) Vezesd vissza a definícióra! Ez a szabály különösen bizonyítási feladatoknál hasznos. 06 Mutasd meg, hogy a háromszög három oldalfelező merőlegese egy pontban metszi egymást! A bizonyítás nem nehéz, ha emlékszünk az oldalfelező merőleges definíciójára. Ugyanis ha U s1 és s2 metszéspontja, akkor AU = BU és BU = CU teljesül, amiből AU = CU és ezért U s3-on is rajta van. (4) Vizsgáld meg a szélső eseteket! 07 Legye adott egy tetszőleges ABCD négyszög (5h. ábra). Összekötjük az AD és BC oldal felező pontjait, M-et és N-et. Melyik nagyobb: MN vagy 0,5(AB + DC)? Tekintsük először a szélső esetet, amikor a két végpont, vagyis C és D egybeesnek (5i. ábra). Ebben az esetben a párhuzamos szelők tételéből vagy hasonló háromszögek segítségével következik: MN = 0,5 · AB. Most az általános esetet visszavezethetjük a szélső esetre. Az 5j. ábrán a négyszöget a BD átló két háromszögre bontja. Ha berajzoljuk még az MK || AB és KN || DC szakaszokat, akkor az ABD és CDB háromszög is a szélső esetek felel meg. Ezért fennáll: 1 AB 2 1 KN DC 2 Ebből a háromszög-egyenlőtlenség miatt következik: MK MN MK KN 1 AB DC , 2 Ezzel a problémát megoldottuk. Sőt még többet is mondhatunk: egyenlőség pontosan akkor áll fenn, ha MN || AB, ami azt jelenti, hogy az ABCD négyszög trapéz, amelynek alapjai AB és DC. (5) Változtasd meg a feltételeket! Változtasd meg az adatokat! Változtasd meg a vázlatot! Játssz a feltételekkel! Ezáltal az adatok egymástól való függése felismerhetővé válik, láthatók lesznek speciális vagy szélső esetek, az észre nem vett esetek felfedezhetőek stb. Témaspecifikus szabályok M Ezek korlátozott anyagrészre vonatkoznak. Példaként szolgálnak a 66. oldalon felsorolt célirányos képletátalakítási szabályok. További példaként bemutatunk néhány szabályt az elemi geometria területéről: – Készíts vázlatot (amely úgy néz ki, mintha a feladatot már megoldottad volna)! – Jelöld a vázlaton a megadott adatokat! – Próbálj ismert szerkesztési eljárásokat alkalmazni! – Próbál segédvonalakkal olyan alakzatokat létrehozni, amelyek továbbsegítenek! (Köss össze pontokat, hosszabbítsd meg a vonalakat, húzz párhuzamosokat vagy merőlegeseket stb.!) 08 (WALSCH-WEBER 1975, 199. o. nyomán): Szerkessz trapézt, ha adott a, c, d és β (a || c). Vázlatkészítés és a megadott adatok jelölése utá észrevesszük, hogy az ismert szerkesztési eljárások egyike sem segít tovább. Próbáljuk meg segédvonalakkal. Kézenfekvő az átlók berajzolása. Ám azt is megállapíthatjuk, hogy sem az egyik, sem a másik átló nem segít. Egyéb segédvonalakkal próbálkozunk: Mindkét variáció célhoz vezet. Példa különböző heurisztikus cselekmények együtthatására a tanításban: a kerületi szögek tételének feldolgozása Ezen példa bemutatásánál arra a , amelyet STEINHÖFEL/REICHOLD (1971) a bizonyítás feldolgozására adott meg. A szerzők a folyamatba három fázist különböztetnek meg: a) A tétel felismerése – sejtés megtalálása. b b) A bizonyítás megtalálása. Ennek a fázisnak a részlépései többek között: a bizonyítás szükségességének igénye, a sejtés logikai elemzése, a sejtés besorolása az eddig megszerzett matematikai tudások közé, lehetséges bizonyítási eszközök megtalálása (tételek és definíciók, amelyek a bizonyításhoz szóba jöhetnek), a bizonyítási ötlet megtalálása. Ennek a fázisnak a végére a bizonyítást lényegében meg kell találni, anélkül, hogy azt tökéletesen le tudnánk írni. c) A bizonyítás leírása – a következtetési lánc többé-kevésbé hiánytalan leírása a feltételektől az állításig. Ez a három fázis a gyakorlatban gyakran erősen egymásba folyik, a következőkben azonban külön tárgyaljuk őket. A kerületi szögek tételének következő feldolgozása során feltesszük, hogy a tanulók a háromszög szögeire vonatkozó néhány tétellel és a körrel kapcsolatos alapfogalmakkal tisztában vannak. Ugyanígy feltételezzük, hogy a tanár a kör húrja fölé rajzolt kerületi szög fogalmát már elmagyarázta. a) A tétel felismerése: A tanár kiosztja egy kör és abba berajzolt húr fénymásolatát (A,13), és megkéri a diákokat, hogy rajzoljanak minél több kerületi szöget a húrhoz. Aki a legnagyobb kerületi szöget megtalálja, az nyer. Ebből szinte bizonyosan adódik a sejtés, hogy az AB fölé írt összes kerületi szög egyenlő nagyságú. (Az a felszólítás, hogy méréssel állapítsuk meg, hogy az AB fölé írt összes kerületi szög egyenlő nagyságú, kevésbé lenne hasznos, mivel ezáltal megfosztanánk a diákokat az általuk megtalált sejtéstől.) b) A bizonyítás megtalálása: Abból indulunk ki, hogy a diákokban legalább egy minimális igény van a bizonyításra (különben a további munka meglehetősen értelmetlen.) A sejtés logikai elemzése megköveteli, hogy a sejtést Ha – akkor formában fogalmazzuk meg (különben nem tudjuk, hogy a bizonyításban hogyan …)Ez a tanulók számára nem egyszerű, és tanári segítséget igényel. A sejtést átfogalmazása Ha – akkor formára ugyanis meglehetősen erős nyelvi átalakítást igényel. Lényegében két lehetőség van: – Ha APB és AP’B az AB húr fölé írt kerületi szögek, akkor APB = AP’B – Ha AB a kör egy húrja, akkor létezik egy olyan rögzített φ szög, hogy APB = φ minden a körvonalon fekvő P pontra. Mindkét megfogalmazás A következőkben mi csak egy bizonyítást írunk le vázlatosan, amely a második megfogalmazásnak felel meg. Mielőtt azonban tovább lépnénk, érdemes a kiindulási feltételt és az állítást írásban rögzíteni: Feltétel: AB a kör egy húrja. Állítás: Létezik egy olyan rögzített φ szög, hogy APB = φ minden a körvonalon fekvő P pontra. A sejtés besorolása az eddig megszerzett matematikai tudások közé ismét csak nem egyszerű. A sejtésnek valószínűleg a körhöz és a háromszög szögeivel van valamiféle kapcsolata (mivel az APB háromszög egy szögét vizsgáljuk). Ezáltal a bizonyítási eszközöket (definíciók, tételek) is könnyű megtalálni. A tanár lehetőséget adhat arra, hogy a diákok felsorolják a körre és a háromszög szögeire vonatkozó ismert definíciókat és tételeket. Felírhatja ezeket a táblára, így egységben a már felrajzolt vázlattal körülbelül a következő táblaképet kaphatjuk: (1) A kör azon pontok halmaza, amelyek egy adott M ponttól egyenlő r távolságra vannak. (2) Egy háromszög belső szögeinek összege 180˚. (3) Egy háromszög külső szöge egyenlő a két nem mellette fekvő belső szög összegével. (4) Az egyenlőszárú háromszög alapon fekvő szögei egyenlő nagyságúak. A táblára minden további nélkül több definíció vagy tétel is felkerülhet, mint ami végül is felhasználásra kerül. A tanár ügyes válogatása azonban megkönnyítheti a bizonyítási ötletet a diákok számára. (Mindazonáltal ebben van egy manipulatív momentum.) Hogyan jut el az ember egy bizonyítási ötlethez? Itt lépnek be a heurisztikus megfontolások, amelyeket a tanár „támogatni” tud anélkül, hogy azonnal elárulná a tanulóknak a trükköt. Vázlatosan bemutatunk egyet a számtalan heurisztikus megfontolás közül: Az APB szöget szeretnénk egy adott szög nagyságával összehasonlítani. Az egyetlen rögzített szögek, amelyek az ábrán kínálkoznak, az ABM háromszög szögei, és itt azok közül is különösen az AMB szög, mert ez, mint ahogy APB szög is, az AB húr fülé írt szög. Milyen összefüggés van APB és AMB szög között? A mérések ahhoz a sejtéshez vezethetnek, hogy AMB = 2 · APB. Ha ez a sejtés helyes, akkor eredeti sejtésünket is bizonyítottuk volna (φ = 0,5 · AMB). Hogyan tudnánk megmutatni, hogy AMB = 2 · APB? Próbáljuk meg először ezt abban speciális esetben bizonyítani, amikor ABP háromszög egyenlő szárú (5k. ábra). A rövidség kedvéért vezessük be az APB = α, AMB = β jelölést. Így azt kell bizonyítani, hogy β = 2α. Az ábra alapján kézenfekvőnek tűnik, hogy berajzoljuk az ABP egyenlő szárú háromszög magasságát, és beírjuk α/2 és β/2 szögnagyságot. A β és α közötti összefüggés keresésekor (heurisztikus szabály: Keress összefüggéseket!), észrevehetjük, hogy AMF az AMP háromszög egyik külső szöge. Hogy alkalmazni tudjuk a külső szögekre vonatkozó tételt, szükségünk van a PAM szög nagyságára. A kör definíciójából következik, hogy MA = MP (heurisztikus szabály: Vezesd vissza a definícióra!), és ezért az AMP egyenlő szárú, vagyis PAM = α/2. A külső szögekre vonatkozó tétel alapján β/2 = α/2 + α/2 = α. Ezen megfontolások viszonylag könnyen átvihetők az általános esetre (5.l. ábra) Analóg módon adódik: β1 = 2α1 és β2 = 2α2 , vagyis β = β1 + β2 = 2α1 + 2α2 = 2(α1 + α2) = 2α. P Ezzel készen vagyunk a bizonyítással? Ha P-t végigfuttatjuk a körvonalon, (heurisztikus szabály: Változtasd meg a feltételeket!), észrevesszük, hogy a megtalált bizonyítás csak akkor működik, ha P sem jobbra, sem balra nincs túl messze, azaz M az ABP háromszögön belül fekszik. Tehát újabb eseteket kell megkülönböztetnünk. Szimmeria-okokból elég az 5.m ábra esetét vizsgálni. Ezt az esetet a tanulók egyedül is feldolgozhatják, mivel a fenti megfontolások analóg módon elvégezhetők. * F Ha egy bizonyításnál esetszétválasztás fordul elő, nem gondoljuk, hogy minden esettel részletesen foglakozni kell. Azonban a vizsgálandó eseteket mind fel kell sorolni, vagy legalábbis megállapítani, hogy még további eseteket kellene vizsgálni. * Az eredeti szöveg: Weitere heuristische Regeln PÓLYA hat in seinen Arbeiten (vor allem 1949) einige heuristische Regeln formuliert, die in der Mathematik universell einsetzbar sind und im Unterricht gelegentlich nützlich sein können. Wir zählen einige dieser Regeln auf und illustrieren sie an Beispielen. (1) Führe die Aufgabe auf Bekanntes zurück! Kennst du eine ähnliche oder verwandte Aufgabe, die du schon gelöst hast? Kannst du Teile der Aufgabe bereits lösen? 04 Von einem Dreieck kennt man a , und ß. Berechne b und c! Wir nehmen dabei an, dass die Schüler rechtwinkelige, aber noch nicht schiefwinkelige Dreiecke auflösen können. Die Aufgabe kann durch Zerlegung des Dreiecks in zwei rechtwinkelige Dreiecke auf Bekanntes zurückgeführt werden. (2) Suche Zusammnenhänge auf! Kennst oder siehst du funktionale, algebraische, logische oder andere Abhängigkeiten? Wie verändert sich das eine, wenn sich das andere verändert? 05 Von einem am waagrechten Boden vor einem Turm liegenden Bebachtungspunkt aus erschein' das untere Ende eines Turmfensters, das a Meter über dem Boden liegt, unter dem Höhenwinkel , das obere Ende unter dem Höhenwinkel ß . Wie hoch ist das Turmfenster? Wenn man keinen Lösungsweg sieht, kann man zunächst versuchen, irgendwelche algebraischen Beziehungen zwischen x, a, αund ß anzugeben. Direkte Beziehungen sind nicht ersichtlich. Führt man noch y ein, kann man die Beziehungen a = y · tg und a+x = y · tgß erkennen. Daraus kann man u.U. ersehen, dass man durch Elimination von y die gesuchte Größe x erhält. (3) Gehe auf Definitionen zurück! Diese Regel ist besonders bei Beweisaufgaben nützlich. 06 Zeige, dass die drei Seitensymmetralen eines Dreiecks sich in einem Punkt schneiden! Der Beweis ist nicht schwer, wenn man sich der Definition der Seitensymmetrale entsinnt. Denn ist U der Schnittpunkt von s1 und s2, dann gilt AU = BU und BU = CU, somit AU = CU und somit liegt U auch auf der s3. (4) Betrachte Grenzfälle (Extremfälle)! 07 Gegeben sei ein beliebiges Viereck ABCD (Fig. 5h). Wir verbinden die Mittelpunkte M, N der Seiten [A, D] und [B, C]. Was ist größer: MN oder 0,5(AB + DC)? Wir betrachten zuerst den Grenzfall, dass zwei Endpunkte, etwa C und D, zusammenfallen (Fig. 5i). In diesem Fall folgt mit der Hilfe des Strahlensatzes oder ählicher Dreiecke: MN 1 AB 2 Der allgemeine Fall kann nun auf den Grenzfall zurückgeführt werden. In Fig.5j wird das Viereck durch die Diagonale [B, D] in zwei Dreiecke zerlegt. Zeichnet man noch die Strecken [M, K] || [A, B] és [K, N] || [D, C] ein, so entspricht jedes der beiden Dreiecke ABD und CDB dem Grenzfall. Es gilt daher: 1 AB 2 1 KN DC 2 Daraus folg nach der Dreiecksungleichung: MK 1 AB DC , 2 womit das Problem gelöst ist. Wir können sogar mehr sagen: Gleichheit tritt genau dann MN MK KN ein, wenn [M, N] || [A, B] , d. h. wenn das Viereck ABCD ein Trapez mit der Parallelseiten [A, B] und [D, C] ist. (5) Variiere die Bedingungen: Verändere die Angaben! Verändere die Skizze! Spiele mit den Angaben! Dabei können Abhängigkeiten erkannt werden, Spezial- oder Grenzfälle gesehen werden, zunächst übersehene Fälle entdeckt werden usw. A M Stoffspezifische Regeln Diese beziehen sich auf ein begrenztes Stoffgebiet. Beispiele bilden etwa die auf Seite 66 genannten Regeln zum zielgerichteten Formelumformen. Als weitere Beispiele führen wir einige Regeln der Elementargeornetrie an: – Fertige eine Skizze an (in der so getan wird, als ob die Aufgabe schon gelöst wäre)! – Kennzeichne in der Skizze die gegebenen Größen! – Versuche, bekannte Konstruktionsverfahren anzuwenden! – Versuche, durch Hilfslinien solche Figuren zu erzeugen, die weiterhelfen! (Verbinde Punkte, verlängere Linien, ziehe Parallele oder Normale etc.) 08 (nach WALSCH-WEBER 1975, S. 199): Konstruiere ein Trapez aus a,c,d und ß (a II c). Nach Anfertigung einer Skizze und Kennzeichnung der gegebenen Größen merken wir, dass keines der bekannten Konstruktionsverfahren weiterhilft. Wir versuchen es mit Hilfslinien. Naheliegend ist das Einzeichnen der Diagonalen. Wir stellen jedoch fest, dass weder die eine noch die andere Diagonale weiterhilft. Wir versuchen es mit anderen Hilfslinien: Beide Varienten führen zum Ziel. Ein Beispiel für das Zusammenwirken verschiedener heuristischer Aktivitäten im Unterricht : Erarbeitung des Peripheriewinkelsatzes Bei der Darstellung dieses Beispiels lassen wir uns durch ein Phasenschema anregen, das von STEINHÖFEL/REICHOLD (1971) zur Erarbeitung von Beweisen angegeben wurde. Die Autoren unterscheiden in diesem Prozeß drei Phasen: (a) Satzfindung, d.h. Auffinden einer Vermutung. (b) Beweisfindung. Teilschritte dieser Phase sind u.a.: Motivierung der Beweisnotwendigkeit, logische Analyse der Vermutung, Einordnung der Vermutung in das bisher erworbene mathematische Wissen, Auffinden möglicher Beweismittel (Sätze und Definitionen, die für einen Beweis in Frage kommen), Auffinden einer Beweisidee. Am Ende dieser Phase soll ein Beweis im wesentlichen gefunden sein, ohne dass man ihn bereits lückenlos darstellen kann. (c) Beweisdarstellung, d.h. mehr oder weniger lückenlose Darstellung der logischen Folgerungskette von den Voraussetzungen bis zur Behauptung. Diese drei Schritte fließen in der Praxis oft stark ineinander, sollen im folgenden aber getrennt erläutert werden. Bei der folgenden Erarbeitung des Peripheriewinkelsatzes setzen wir voraus, dass die Schüler mit einigen Sätzen über Dreieckswinkel sowie mit einigen Grundbegriffen der Kreislehre vertraut sind. Ebenso wollen wir voraussetzen, dass der Lehrer den Begriff "Peripheriewinkel über einer Kreissehne" schon erklärt hat. (a) Satzfindung: Der Lehrer teilt Kopien eines Kreises mit eingezeichneter Sehne (A,13] aus und fordert die Schüler auf, möglichst viele Peripheriewinkel über der Sehne zu zeichnen. Wer den größten Peripheriewinkel findet, hat gewonnen. Daraus ergibt sich ziemlich sicher die Vermutung, dass alle Peripheriewinkel über [A,B] gleich groß sind. (Die Aufforderung, durch Messung festzustellen, dass alle Peripheriewinkel über [A,B] gleich groß sind, wäre weniger günstig gewesen, da dadurch die von den Schülern zu entdeckende Vermutung vorweggenommen wird.) (b) Beweisfindung: Wir gehen davon aus, dass für die Schüler wenigstens eine gewisse Motivation für einen Beweis vorliegt (ansonsten ist ein Weiterarbeiten ziemlich sinnlos). Die logische Analyse der Vermutung erfordert, die Vermutung in Wenn-dannForm zu bringen (sonst weiß man nicht, wie man bei dem Beweis vorzugehen hat). Dies ist für Schüler nicht einfach und wird der Hilfe des Lehrers bedürfen. Die vorliegende Vermutung in Wenn-dann-Form zu bringen, erfordert nämlich relativ starke sprachliche Umformulierungen. Im wesentlichen gibt es zwei Möglichkeiten: ' – Wenn APB und AP'B Peripheriewinkel über der Sehne [A,B] sind, dann ist APB = AP'B – Wenn [A,B] Sehne eines Kreises ist, dann gibt es ein festes Winkelmaß , sodass APB = für alle Punkte P auf der Kreislinie. Beide Formulierungen können zu einem Beweis herangezogen werden. Wir skizzieren im folgenden aber nur einen Beweis, der der zweiten Formulierung entspricht. Bevor weitergeschritten wird, ist es günstig, Voraussetzung und Behauptung schriftlich festzuhalten: Voraussetzung: [A,B] ist Sehne eines Kreises. Behauptung: Es gibt ein festes Winkelmaß , sodass APB = für alle P auf der Kreislinie. Die Einordnung der Vermutung in das bisher erworbene mathematische Wissen ist wiederum leicht. Die Vermutung hat höchstwahrscheinlich etwas mit dem Kreis und mit Winkeln in Dreiecken zu tun (da ja ein Winkel im Dreieck APB betrachtet wird). Damit sind auch die Beweismittel (Definitionen, Sätze) leicht zu finden. Der Lehrer kann die Schüler veranlassen, bekannte Definitionen und Sätze über den Kreis und über Winkel in Dreiecken aufzuzählen. Er kann diese an die Tafel schreiben, sodass im Verein mit der schon gezeichneten Skizze etwa folgendes Tafelbild entsteht: Dabei können an der Tafel ohne weiteres mehr Definitionen oder Sätze stehen als (1) Der Kreis von einem Abstand r haben. ist die gegebenen (2) Die Summe Dreiecks beträgt 180. (3) Ein der Innenwinkel. Außenwinkel Summe (4) Die Basiswinkel Dreiecks sind gleich groß. letzten Menge Punkt der eines der aller M Punkte, die den gleichen Innenwinkel Dreiecks beiden eines eines ist gleich nichtanliegenden gleichschenkligen Endes gebraucht werden. Eine geschickte Auswahl durch den Lehrer kann den Schülern jedoch das Auffinden einer Beweisidee erleichtern (allerdings liegt darin auch ein manipulatives Moment). Wie kann man zu einer Beweisidee kommen? Hier setzen nun heuristische Überlegungen ein, die der Lehrer unterstützen kann, ohne den Schülern gleich den "Trick" zu verraten. Wir skizzieren eine von vielen möglichen heuristischen Überlegungen: Wir wollen ja den Winkel APB mit einem festen Winkel vergleichen. Die einzigen festen Winkel, die sich in der Figur anbieten, sind die Winkel im Dreieck ABM und hier wiederum bietet sich besonders der Winkel AMB an, weil dieser wie APB über der Sehne [A,B] liegt. Wie hängt zur Vermutung führen: APB mit AMB zusammen? Messungen können AMB = 2 · APB. Falls diese Vermutung stimmt, hätten wir auch unsere ursprüngliche Vermutung bewiesen (mit φ = ½ · können wir zeigen, dass AMB = 2 · AMB). Wie APB? Versuchen wir zunächst, dies in dem Spezialfall zu beweisen, dass das Dreieck ABP gleichschenkelig ist (Fig. 5k). Wir setzen zur Abkürzung APB = α und AMB = β. Somit ist β= 2α zu beweisen. In der Figur ist es naheliegend, die Höhe des gleichschenkeligen Dreiecks ABP einzuzeichnen und die Winkelmaße α/2 und β/2 einzutragen. Auf der Suche nach einem Zusammenhang zwischen β und α (heuristische Regel: Suche Zusammenhänge auf!) kann man entdecken, daß AMF ein Außenwinkel P des Dreiecks AMP ist. Um den Satz über die Außenwinkel anwenden zu können, braucht man das Maß des Winkels PAM. Aus der Definition des Kreises folgt MA=MP (heuristische Regel: Gehe zurück auf Definitionen!), somit ist das Dreieck AMP gleichschenkelig und somit PAM = α/2. Nach dem Satz über die Außenwinkel folgt β/2 = α/2 + α/2 = α. Diese Überlegungen lassen sich relativ leicht auf den allgemeinen Fall übertragen (Fig. 5.l). Es ergibt sich in analoger Weise β1 = 2α1 und β2 = 2α2 somit β = β1 + β2 = 2α1 + 2α2 = 2(α1 + α2) = 2α. Sind wir damit mit dem Beweis fertig? Lassen wir P auf der Kreislinie wandern (heuristische Regel: Variiere die Bedingungen!), bemerken wir, daß der gefundene Beweis nur funktioniert, wenn der Punkt P nicht zu weit links oder rechts liegt, d.h. M nicht außerhalb des Dreiecks ABP liegt. Es sind also noch weitere Fälle zu betrachten. Aus Symmetriegründen genügt es, den Fall in Fig.5m zu betrachten. Dieser Fall kann von den Schülern selbst bearbeitet werden, da man den obigen Überlegungen analog vorgehen kann.* * Falls bei einem Beweis Fallunterscheidungen auftreten, meinen wir nicht, daß man unbedingt alle Fälle behandeln muß. Man sollte aber alle zu behandelnden Fälle aufzählen oder wenigstens feststellen, daß noch weitere Fälle zu behandeln wären. A fordító kommentárja: Az eredeti szöveg egy gimmáziumi diákoknak íródott tankönyvből származik.Ennek tudható be, hogy a fordítás hangvétele fiatalosabb, lezserebb, mint a megszokott szakszövegeké. A nyelvezet ebből adódóan személyesebb ,sok benne a felszólítás ,az olvasóval együtt készíti el a feladatok a szerző, próbál együtt gondolkozásra sarkallni. Ennek megfelelően, a célközönségnek én is diákokat válaszottam, és próbáltam hasonló módon elkészíteni a fordítást. Ezt a fordítást nem tartottam túlságosan nehéznek, hiszen németről magyarra kellett fordítanom, ami jóval könnyebb mintha ez fordítva történne. A fordításomhoz több, hasonló hangvételű és tartalmú szöveget használtam segítségképpen. Források: Halász Előd: Német-magyar kéziszótár, Akadémiai Kiadó, Budapest, 1991. Kornya László: Német-magyar magyar-német matematikai kifejezés- és szöveggyűjtemény, Tankönyvkiadó, Budapest, 1992. MoBiDictionary - On-line szótár, http://mobidic.hu Wikipedia, Die freie Enzyklopedie, http://de.wikipedia.org/wiki/Wiki