4. SA

4. Schularbeit aus Mathematik und angewandter Mathematik
1 bl – riegler
Mittwoch, 11. Mai 2016
Gruppe A
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
a)
b)
c)
2.
a)
b)
c)
3.
a)
b)
c)
4.
a)
b)
Eine Firma hat bei einer Produktionsmenge von 8 000 Stk. Kosten von € 880.000,--, bei einer Menge von
10 000 Stk. betragen die Kosten schon 1.020.000,--. Berechnen Sie die proportionalen Kosten und die
Fixkosten. Stellen Sie die lineare Kostenfunktion auf.
k = Error! = 70 = k
880 000 = 70 · 8 000 + F  F = 320 000
K(x) = 70x + 320 000
Eine Firma hat Fixkosten
von € 30.000,-- und
proportionale Kosten von
15 €/Stk. Sie verkauft das
Produkt um 18 €/Stk.
Berechnen Sie den
Break-Even-Punkt und
den Gewinn bei einer
verkauften Stückzahl von 12 000 Stk..
K(x) = 15x + 30 000 p = 18
15x + 30 000 = 18x  x = 10 000
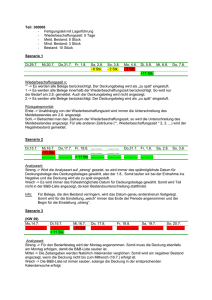
G(12 000) = 18 · 12 000 – (15 · 12 000 + 30 000) = 6.000,-Die nebenstehende Graphik zeigt den Verlauf einer Kostenfunktion. Ermitteln Sie die proportionalen
Kosten und zeichnen Sie den Graph einer Erlösfunktion so ein, dass der Break-Even bei einer Menge von
20 ME liegt. Ermitteln Sie dann den Preis für diese Situation.
k = Error! = 10 GE/ME
p = Error! = 20 GE/ME
Geben Sie den angegebenen Term in der jeweils anderen (Wurzel- bzw. Potenz mit rationalem
Exponenten) Darstellung an und vereinfachen Sie so weit wie möglich:
b4/5 =
5;b4
5;x3 = x3/5
Error! = a20/5 = a4
Vereinfachen Sie so weit wie möglich:
Error! = NR: x: Error! y: Error! daher R = Error!
Zwischen den Größen a, b und c gilt die Beziehung a = b 0,3 c .
Berechnen Sie die prozentuale Änderung von a, wenn b um 80 % größer wird.
1,80,3 = 1,193
a wird um 19,3 % größer
Lösen Sie das System in ℝ2
5x + 3y = 22
4x – 8y = 80
52x = 416  x = 8 und 40 + 3y = 22  y = –6 L = {(8 / –6)}
Lösen Sie das System 3x + 2y = 15 und y = 5 – x
3x + 2(5 – x) =15 x + 10 = 15  x = 5 y = 0
Ermitteln Sie den Parameter a so, dass das System
3x – 2y = 10
ax – 14y = 70
unendlich viele Lösungen hat.
a = 21
Eine Firma kauft zwei Rohstoffe A und B.
Bei der ersten Bestellung kauft sie 300 Stk. von A und 200 Stk. von B und bezahlt € 25.500,--.
Bei einer neuerlichen Bestellung kauft sie 800 Stk. von A und 100 Stk. von B und bezahlt € 42.000,--.
Stellen Sie ein Gleichungssystem auf, mit dem man die Stückpreise a und b der Rohstoffe A und B
berechnen kann.
300 a + 200 b = 25 500
800 a + 100 b = 42 000
Max fährt um 9:00 mit dem Auto mit einer Geschwindigkeit von 80 km/h von Micheldorf in das 260 km
entfernte Wehofen. Susanne fährt um 10:00 von Wehofen nach Micheldorf. Sie fährt durchschnittlich
100 km/h. Berechnen Sie, wann und wo die beiden aneinander vorbeifahren.
m = 80(t – 9)
s = –100(t – 10) + 260
80t – 720 = –100t + 1260  180 t = 1980  t = 11
m(11) = 80 · 2 = 160 um 11:00 Uhr, 160 km von Micheldorf entfernt
4. Schularbeit aus Mathematik und angewandter Mathematik
1 bl – riegler
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
Mittwoch, 11. Mai 2016
Gruppe B
1.
a)
b)
c)
2.
a)
b)
c)
3.
a)
b)
c)
4.
a)
b)
Eine Firma hat bei einer Produktionsmenge von 8 000 Stk. Kosten von € 860.000,--, bei einer Menge von
10 000 Stk. betragen die Kosten schon 980.000,--. Berechnen Sie die proportionalen Kosten und die
Fixkosten. Stellen Sie die lineare Kostenfunktion auf.
k = Error! = 60 = k
860 000 = 60 · 8 000 + F  F = 380 000
K(x) = 60x + 380 000
Eine Firma hat Fixkosten
von € 30.000,-- und
proportionale Kosten von
15 €/Stk. Sie verkauft das
Produkt um 21 €/Stk.
Berechnen Sie den
Break-Even-Punkt und
den Gewinn bei einer
verkauften Stückzahl von 12 000 Stk..
K(x) = 15x + 30 000 p = 21
15x + 30 000 = 21x  x = 5 000
G(12 000) = 21 · 12 000 – (15 · 12 000 + 30 000) = 42.000,-Die nebenstehende Graphik zeigt den Verlauf einer Kostenfunktion. Ermitteln Sie die proportionalen
Kosten und zeichnen Sie den Graph einer Erlösfunktion so ein, dass der Break-Even bei einer Menge von
20 ME liegt. Ermitteln Sie dann den Preis für diese Situation.
k = Error! = 10 GE/ME
p = Error! = 20 GE/ME
Geben Sie den angegebenen Term in der jeweils anderen (Wurzel- bzw. Potenz mit rationalem
Exponenten) Darstellung an und vereinfachen Sie so weit wie möglich:
b4/7 =
7;b4
7;x3 = x3/7
Error! = a10/5 = a2
Vereinfachen Sie so weit wie möglich:
Error! = NR: x: Error! y: Error! daher R = Error!
Zwischen den Größen a, b und c gilt die Beziehung a = b 0,3 c .
Berechnen Sie die prozentuale Änderung von a, wenn b um 60 % größer wird.
1,60,3 = 1,151
a wird um 15,1 % größer
Lösen Sie das System in ℝ2
5x + 3y = 25
4x – 8y = 72
52x = 416  x = 8 und 40 + 3y = 25  y = –5 L = {(8 / –5)}
Lösen Sie das System 3x + 2y = 18 und y = 6 – x
3x + 2(6 – x) = 15 x + 12 = 18  x = 6 y = 0
Ermitteln Sie den Parameter a so, dass das System
3x – 2y = 10
ax – 16y = 80
unendlich viele Lösungen hat.
a = 24
Eine Firma kauft zwei Rohstoffe A und B.
Bei der ersten Bestellung kauft sie 30 Stk. von A und 20 Stk. von B und bezahlt € 2.550,--.
Bei einer neuerlichen Bestellung kauft sie 80 Stk. von A und 10 Stk. von B und bezahlt € 4.200,--.
Stellen Sie ein Gleichungssystem auf, mit dem man die Stückpreise a und b der Rohstoffe A und B
berechnen kann.
30 a + 20 b = 2 550
80 a + 10 b = 4 200
Max fährt um 10:00 mit dem Auto mit einer Geschwindigkeit von 80 km/h von Micheldorf in das 460 km
entfernte Wehofen. Susanne fährt um 9:00 von Wehofen nach Micheldorf. Sie fährt durchschnittlich
100 km/h. Berechnen Sie, wann und wo die beiden aneinander vorbeifahren.
m = 80(t – 10)
s = –100(t – 9) + 460
80t – 800 = –100t + 1360  180 t = 2160  t = 12
m(12) = 80 · 2 = 160 um 12:00 Uhr, 160 km von Micheldorf entfernt
4. Schularbeit aus Mathematik und angewandter Mathematik
1 bl – riegler
Mittwoch, 11. Mai 2016
Gruppe A
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
a)
Eine Firma hat bei einer Produktionsmenge von 8 000 Stk. Kosten von € 880.000,--, bei einer Menge von
10 000 Stk. betragen die Kosten schon 1.020.000,--. Berechnen Sie die proportionalen Kosten und die
Fixkosten. Stellen Sie die lineare Kostenfunktion auf.
b)
Eine Firma hat Fixkosten von € 30.000,-- und proportionale Kosten von 15 €/Stk. Sie verkauft das
Produkt um 18 €/Stk. Berechnen Sie den Break-Even-Punkt und den Gewinn bei einer verkauften
Stückzahl von 12 000 Stk..
c)
Die nebenstehende Graphik zeigt den Verlauf einer Kostenfunktion. Ermitteln Sie die proportionalen
Kosten und zeichnen Sie den Graph einer Erlösfunktion so ein, dass der Break-Even bei einer Menge von
20 ME liegt. Ermitteln Sie dann den Preis für diese Situation.
A
2.
a)
Geben Sie den angegebenen Term in der jeweils anderen (Wurzel- bzw. Potenz mit rationalem
Exponenten) Darstellung an und vereinfachen Sie so weit wie möglich:
b4/5 =
5;x3
=
Error! =
b)
Vereinfachen Sie so weit wie möglich:
Error! =
c)
Zwischen den Größen a, b und c gilt die Beziehung a = b0,3 c .
Berechnen Sie die prozentuale Änderung von a, wenn b um 80 % größer wird.
A
3.
a)
Lösen Sie das System in ℝ2
5x + 3y = 22
4x – 8y = 80
b)
Lösen Sie das System 3x + 2y = 15 und y = 5 – x
c)
Ermitteln Sie den Parameter a so, dass das System
3x – 2y = 10
ax – 14y = 70
unendlich viele Lösungen hat.
A
4.
a)
Eine Firma kauft zwei Rohstoffe A und B.
Bei der ersten Bestellung kauft sie 300 Stk. von A und 200 Stk. von B und bezahlt € 25.500,--.
Bei einer neuerlichen Bestellung kauft sie 800 Stk. von A und 100 Stk. von B und bezahlt € 42.000,--.
Stellen Sie ein Gleichungssystem auf, mit dem man die Stückpreise a und b der Rohstoffe A und B
berechnen kann.
b)
Max fährt um 9:00 mit dem Auto mit einer Geschwindigkeit von 80 km/h von Micheldorf in das 260 km
entfernte Wehofen. Susanne fährt um 10:00 von Wehofen nach Micheldorf. Sie fährt durchschnittlich
100 km/h. Berechnen Sie, wann und wo die beiden aneinander vorbeifahren.
4. Schularbeit aus Mathematik und angewandter Mathematik
1 bl – riegler
Mittwoch, 11. Mai 2016
Gruppe B
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
a)
Eine Firma hat bei einer Produktionsmenge von 8 000 Stk. Kosten von € 860.000,--, bei einer Menge von
10 000 Stk. betragen die Kosten schon 980.000,--. Berechnen Sie die proportionalen Kosten und die
Fixkosten. Stellen Sie die lineare Kostenfunktion auf.
b)
Eine Firma hat Fixkosten von € 30.000,-- und proportionale Kosten von 15 €/Stk. Sie verkauft das
Produkt um 21 €/Stk. Berechnen Sie den Break-Even-Punkt und den Gewinn bei einer verkauften
Stückzahl von 12 000 Stk..
c)
Die nebenstehende Graphik zeigt den Verlauf einer Kostenfunktion. Ermitteln Sie die proportionalen
Kosten und zeichnen Sie den Graph einer Erlösfunktion so ein, dass der Break-Even bei einer Menge von
20 ME liegt. Ermitteln Sie dann den Preis für diese Situation.
A
2.
a)
Geben Sie den angegebenen Term in der jeweils anderen (Wurzel- bzw. Potenz mit rationalem
Exponenten) Darstellung an und vereinfachen Sie so weit wie möglich:
b4/7 =
7;x3
=
Error! =
b)
Vereinfachen Sie so weit wie möglich:
Error! =
c)
Zwischen den Größen a, b und c gilt die Beziehung a = b 0,3 c .
Berechnen Sie die prozentuale Änderung von a, wenn b um 60 % größer wird.
B
3.
a)
Lösen Sie das System in ℝ2
5x + 3y = 25
4x – 8y = 72
b)
Lösen Sie das System 3x + 2y = 18 und y = 6 – x
c)
Ermitteln Sie den Parameter a so, dass das System
3x – 2y = 10
ax – 16y = 80
unendlich viele Lösungen hat.
B
4.
a)
Eine Firma kauft zwei Rohstoffe A und B.
Bei der ersten Bestellung kauft sie 30 Stk. von A und 20 Stk. von B und bezahlt € 2.550,--.
Bei einer neuerlichen Bestellung kauft sie 80 Stk. von A und 10 Stk. von B und bezahlt € 4.200,--.
Stellen Sie ein Gleichungssystem auf, mit dem man die Stückpreise a und b der Rohstoffe A und B
berechnen kann.
b)
Max fährt um 10:00 mit dem Auto mit einer Geschwindigkeit von 80 km/h von Micheldorf in das 460 km
entfernte Wehofen. Susanne fährt um 9:00 von Wehofen nach Micheldorf. Sie fährt durchschnittlich
100 km/h. Berechnen Sie, wann und wo die beiden aneinander vorbeifahren.