Details Test LU 16

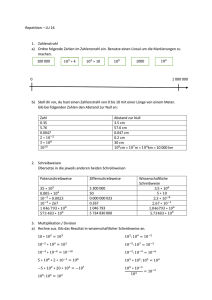
Test – LU 16
-ohne Taschenrechner-
40 Mins
1. Zahlenstrahl
a) Ordne folgende Zahlen im Zahlenstrahl ein. Ziehe dazu jeweils eine Linie von der Zahl zur
Markierung auf dem Zahlenstrahl.
1 000 000
106 ∗ 6
105 ∗ 10
105
3 000 000
107
10 000 000
000000
0
b) Stell dir vor, du hast einen Zahlenstrahl welcher bei den Zahlen von 0 bis 10 eine Länge von
100 Meter aufweist.
Gib bei folgenden Zahlen den Abstand zur Null an:
Zahl
0.75
4.76
0.0035
6 ∗ 10−2
4 ∗ 100
1010
Abstand zur Null
2. Schreibweisen
Übersetze in die jeweils anderen beiden Schreibweisen
Potenzschreibweise
Ziffernschreibweise
Wissenschaftliche
Schreibweise
35 ∗ 104
0.045 ∗ 104
10−4 ∗ 0.0103
10−3 ∗ 2672
1 444 555 ∗ 100
500 484 ∗ 104
3. Multiplikation / Division
a) Rechne aus. Gib das Resultat als Zehnerpotenz an.
10 ∗ 105 =
106 : 105 =
10−7 ∗ 104 =
2 ∗ 102 : 104 ∗ 5 =
10−4 ∗ 10−6 =
10−5 : 102 ∗ 100 =
5 ∗ 103 ∗ 2 ∗ 10−1 =
10−2 : 10−5 =
−0.005 ∗ 105 ∗ 20 ∗ 103 =
105 ∗ 103 : 107 =
105 ∗ 10−3
=
10−4
10𝑎 ∗ 10−𝑏
=
10−𝑐 ∗ 10−𝑑
6
18
√10
=
105 ∗ (105 )3 =
b) Rechne aus. Gib das Resultat in Ziffernschreibweise an.
0.0001 ∗ 1000 =
1 𝐵𝑖𝑙𝑙𝑖𝑎𝑟𝑑𝑒 ∶ 108 =
−4
0.01 ∗ 10 =
0.001: 0.01 =
−4
10 ∗ 10 =
0.01: 10−4 =
3 𝑀𝑖𝑙𝑙𝑖𝑎𝑟𝑑𝑒𝑛 ∗ 0.001: 150 =
1 000: 1 000 000 =
−9
4 𝐵𝑖𝑙𝑙𝑖𝑜𝑛𝑒𝑛 ∗ 5 ∗ 10 =
4. Textaufgaben
a) Ein Wasserstoffatom wiegt 1.6 ∗ 10−27kg. In einem Behälter befinden sich 6.4 kg
Wasserstoff.
i)
Wieviele Wasserstoffatome befinden sich im Behälter?
ii)
Angenommen ein Wasserstoffatom hat einen Durchmesser von 6.4 ∗ 10−10 Meter.
Wie lange wäre eine Kette aus allen aneinandergereihten Wasserstoffatomen des
Behälters?
b) Es gibt in der Milchstrasse – unserer Galaxie – schätzungsweise 100 Milliarden
sonnenähnliche Sterne. Nehmen wir an, dass diese Sterne durchschnittlich gleichschwer sind
wie die Sonne und jeweils Zehn Planeten besitzen. Die Planeten wiegen durchschnittlich
1025kg. Gewicht der Sonne: 2 ∗ 1030 kg. Wie schwer sind demnach alle Sterne und Planeten
unserer Milchstrasse zusammen?