Erwartungswert und Varianz

WR 1
W. Merz
Kapitel 12
Erwartungswert und Varianz
Vorlesung Wahrscheinlichkeitsrechnung I vom 4/10. Juni 2009
W. Merz
Lehrstuhl für Angewandte Mathematik 1
FAU
12.1
WR 1
Der Erwartungswert
W. Merz
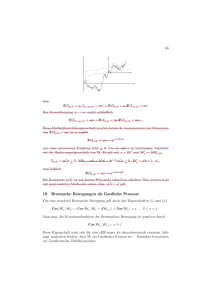
Der Erwartungswert einer Zufallsvariablen X : Ω −→ R wurde
definiert als der Mittelwert der Verteilung P X dieser
Zufallsvariablen:
P
y f X (y ) falls P X diskret mit WF f X
X
R y ∈X
EX = m1 (P ) =
yf X (y )dy
falls P X Dichte f X
Für einen diskreten Wahrscheinlichkeitsraum (Ω, A, P) wurde
eine alternative Berechnungsformel hergeleitet:
X
EX =
X (ω) P{ω}
ω∈Ω
Diese Formel erlaubt die Herleitung spezieller Rechenregeln,
wie z.B. E(X + Y ) = EX + EY .
P-Integral einer Zufallsvariablen:
Z
X (ω)P(dω)
12.2
Das P-Integral
WR 1
W. Merz
• Eine kurze Darstellung der Konstruktion:
• 1. Schritt: Definition des P-Integrals einer Treppenfunktion.
• 2. Schritt: Definition des P-Integrals für allgemeine
Zufallsvariable durch Approximation mit Treppenfunktionen.
• Die wichtigsten Rechenregeln
• Beziehung zwischen P- und L-Integral
12.3
WR 1
Treppenfunktionen
W. Merz
Definition
Eine Zufallsvariable X : Ω −→ R heißt eine Treppenfunktion,
wenn sie nur abzählbar viele Werte annimmt.
Ist X = {x1 , x2 , x3 , . . .} der Wertebereich von X mit paarweise
verschiedenen reellen Zahlen xk , dann bilden die Mengen
Ak = (X = xk ) = {ω ∈ Ω ; X (ω) = xk }
eine Partition von Ω und X besitzt die Darstellung
X
X (ω) =
xk 1Ak (ω)
k
Bezeichung
Diese Darstellung heißt die Normaldarstellung von X .
12.4
WR 1
Treppenfunktionen
W. Merz
Definition
Eine Treppenfunktion
mit der Normaldarstellung
P
X (ω) = k xk 1Ak (ω) heißt P-integrierbar, wenn
X
|xk |P(Ak ) < ∞
k
Ist X P-integrierbar, so heißt
Z
X
X (ω) P(dω) :=
xk P(Ak )
k
das P-Integral von X .
12.5
WR 1
Treppenfunktionen
W. Merz
P-Integral und Mittelwert
Die Verteilung P X einer Treppenfunktion ist diskret mit der
Ergebnismenge X und der Wahrscheinlichkeitsfunktion
f X (xk ) = P X {xk } = P(X = xk ) = P(Ak )
daher ist
Z
X (ω) P(dω) =
X
xk f X (xk ) = m1 (P X )
k
der Mittelwert der Verteilung von X .
12.6
WR 1
Allgemeine Zufallsvariable
W. Merz
Zu einer beliebigen Zufallsvariablen X : Ω −→ R auf einem
Wahrscheinlichkeitsraum (Ω, A, P) gibt es eine Folge (Xn ) von
Treppenfunktionen, die gleichmäßig gegen X konvergiert:
lim kX − Xn k∞ = lim sup |X (ω) − Xn (ω)| = 0
n→∞
n→∞ ω∈Ω
Theorem
Ist wenigstens ein Xn0 P-integrierbar, so sind
R alle Xn
P-integrierbar und die Folge der Integrale Xn (ω) P(dω)
konvergiert.
Der Limes ist unabhängig von der verwendeten Folge und
hängt nur von X und P ab.
Bezeichnung
In diesem Fall heißt X P-integrierbar und
Z
Z
Z
X dP = X (ω) P(dω) = lim
Xn (ω) P(dω)
n→∞
das P-Integral von X .
12.7
Rechenregeln
WR 1
W. Merz
Direkt aus der Definition des P-Integrals einer Treppenfunktion
und anschließend durch Grenzübergang leitet man die
folgenden Eigenschaften ab:
Rechenregeln
1
2
3
R
X (ω) = 1 ist P-integrierbar und es gilt 1 dP = 1.
∗
Ist
R X P-integrierbar und X (ω) ≥ 0 P-fast überall , so ist
X dP ≥ 0.
X ist P-integrierbar genau dann,
R wenn
|X
R |(ω) := |X (ω)|
P-integrierbar ist und es gilt X dP ≤ |X | dP
∗
Eine Aussage gilt „P-fast überall (P-f.ü.)“, wenn sie für alle ω mit der
eventuellen Ausnahme der Elemente einer Menge N mit P(N) = 0 richtig ist.
12.8
Rechenregeln
WR 1
W. Merz
(4) Additionsregel
Sind X und Y P-integrierbar, dann auch jede
Linearkombination aX + bY und es gilt
Z
Z
Z
(aX + bY ) dP = a X dP + b Y dP
(5) Produktregel
Sind X und Y P-integrierbar und stochastisch unabhängig,
dann ist auch das Produkt X · Y P-integrierbar und es gilt
Z
Z
Z
(X · Y ) dP = X dP · Y dP
12.9
WR 1
Rechenregeln
W. Merz
(Ω, A, P) H
H
X
-
(Rn , Bn , P X )
HH
H
HH
Y =G◦X
G
H
HH
j
H
?
(R, B, P Y )
(6) Kompositionssatz
Ist X : Ω −→ Rn ein Zufallsvektor und G : Rn −→ R
P X -integrierbar, dann ist Y = G ◦ X P-integrierbar und es gilt
Z
Z
Z
Y (ω) P(dω) = G(X (ω)) P(dω) = G(y ) P X (dy )
12.10
WR 1
P-Integral und L-Integral
W. Merz
(7) Absolutstetige Verteilungen
Ist P eine absolutstetige Verteilung auf dem Rn mit der Dichte
f (y ) und X : Rn −→ R eine P-integrierbare Zufallsvariable, so
gilt
Z
Z
X (y )P(dy ) =
X (y )f (y )dy
Rn
(8) Diskrete Verteilungen
Ist P eine diskrete Verteilung auf einer abzählbaren
Ergebnismenge X mit der Wahrscheinlichkeitsfunktion f (x)
und Y : X −→ R eine P-integrierbare Zufallsvariable, so gilt
Z
X
Y (x)P(dx) =
Y (x)f (x)
x∈X
12.11
WR 1
Die Momente
W. Merz
Definition
Ist P eine eindimensionale Verteilung und ist die Funktion
x 7−→ x k P-integrierbar, so heißt
Z
mk (P) = x k P(dx)
das k -te Moment der Verteilung P.
Speziell m1 (P) nennen wir den Mittelwert.
Wahrscheinlichkeitsfunktion f (x), so ist nach den
Eigenschaften (7) bzw. (8)
Z
X
mk (P) = y k f (y ) dy bzw. mk (P) =
x k f (x) ,
x∈X
d.h. die Definition ist eine Erweiterung der bisherigen
Konzepte.
12.12
WR 1
Die Momente
W. Merz
Definition
Ist P eine eindimensionale Verteilung und ist die Funktion
x 7−→ (x − m1 (P))k P-integrierbar, so heißt
Z
m̂k (P) = (x − m1 (P))k P(dx)
das k -te zentrale Moment der Verteilung P.
Speziell m̂2 (P) nennen wir die Varianz der Verteilung P.
Ist P absolutstetig mit Dichte f (y ) bzw. diskret mit
Wahrscheinlichkeitsfunktion f (x), so ist nach den
Eigenschaften (7) bzw. (8)
Z
X
m̂k (P) = (y −m1 (P))k f (y ) dy bzw. m̂k (P) =
(x−m1 (P))k f (x) ,
x∈X
d.h. die Definition ist eine Erweiterung der bisherigen
Konzepte.
12.13
WR 1
Der Erwartungswert
W. Merz
Bezeichnung
In der Wahrscheinlichkeitsrechnung nennt man das P-Integral
einer Zufallsvariablen X auf einem Wahrscheinlichkeitsraum
(Ω, A, P) üblicherweise den Erwartungswert:
Z
EX = EP X =
X (ω)P(dω)
Mit G(x) = x ist Y (ω) := G(X (ω)) = X (ω), weshalb nach dem
Kompositionssatz gilt
Z
Z
X (ω)P(dω) = xP X (dx)
Theorem
Der Erwartungswert von X ist der Mittelwert von P X :
EX = m1 (P X )
12.14
WR 1
Der Erwartungswert
W. Merz
Die Momente
Für k = 1, 2, 3, . . . und Gk (x) = x k bzw. Gk (X (ω)) = X k (ω)
ergibt sich entsprechend
E(X k ) = mk (P X )
12.15
Rechenregeln
WR 1
W. Merz
Die Rechenregeln für das P-Integral lauten dann
1
2
3
4
5
6
E1 = 1
|EX | ≤ E|X |
E(aX + bY + c) = a EX + b EY + c
Sind X und Y stochastisch unabhängig, so gilt
E(XY ) = (EX )(EY )
Ist die Zufallsvariable X P-fast überall nichtnegativ, dann
ist EX ≥ 0.
Gilt für zwei Zufallsvariable X ≤ Y P-fast überall, so ist
EX ≤ EY .
12.16
Funktionen von Zufallsvariablen
WR 1
W. Merz
Ist X = (X1 , X2 , . . . , Xn ) ein Zufallsvektor mit absolutstetiger
n-dimensionaler Verteilung P X und Dichte f (x),
sowie Y = G(X1 , X2 , . . . , Xn ) = G ◦ X ,
dann gilt
Z
EY
G(X (ω))P(dω)
=
Z
=
G(x)P X (dx)
Z
=
G(x)f (x)dx
12.17
Berechnung des Erwartungswerts
WR 1
W. Merz
Es gibt also im wesentlichen zwei Methoden zur Berechnung
des Erwartungswerts einer Zufallsvariablen der Form
Y = G ◦ X:
1
2
Berechnung der Dichte g(y ) der Verteilung P Y und des
Mittelwerts
Z
Y
E Y = m1 (P ) = yg(y )dy
Auswertung des Integrals
Z
EY =
G(x)f (x)dx
Die zweite Methode ist auch dann anwendbar, wenn P Y keine
Dichte besitzt.
12.18
Beispiel 1
WR 1
W. Merz
Exercise
In einer Eisdiele wird an jedem Abend bei der Eisfabrik die
gesamte Menge q an Eis für den nächsten Tag bestellt.
Der Einkaufspreis sei p1 Euro pro Mengeneinheit.
Die Tagesnachfrage ist — unter anderem wetterbedingt —
zufällig.
Wir nehmen an, dass es sich um eine exponentiell mit
Parameter λ verteilte Zufallsvariable X handelt.
Gemäß den gesetzlichen Vorschriften darf Eis, das am Abend
noch nicht verkauft ist, nicht gelagert, sondern muss vernichtet
werden.
Welche Menge an Eis muss — bei einem Verkaufspreis von p2
Euro pro Mengeneinheit — bestellt werden, damit der mittlere
Gewinn maximal wird?
12.19
WR 1
Beispiel 1
W. Merz
ω ist zufällig ausgewählter Tag,
X (ω) ist Nachfrage an diesem Tag und q bestellte Menge.
Absatz am Tag ω = min(X (ω), q).
pro Mengeneinheit:
Y (ω) = p2 min(X (ω), q) − p1 q
Erwartungswert des Gewinns:
EY
= E(p2 min(X (ω), q) − p1 q)
= p2 E(min(X (ω), q)) − p1 q
Ansatz zur Berechnung:
min(X (ω), q) = G ◦ X mit G(x) = min(x, q)
12.20
WR 1
Beispiel 1
W. Merz
min(X (ω), q) = G ◦ X mit G(x) = min(x, q)
Z
E min(X (ω), q)
=
G(x)P X (dx)
Z
G(x)f (x)dx
=
Z
∞
min(x, q)λe−λx dx
=
0
Z
=
0
q
xλe−λx dx +
Z
∞
qλe−λx dx
q
12.21
WR 1
Beispiel 1
W. Merz
Z
E min(X (ω), q) =
q
xλe−λx dx +
0
Z
q
xλe−λx dx
0
qλe
q
=⇒
−λx
∞
qλe−λx dx
q
Z q
q
x(−e−λx ) 0 −
−e−λx dx
0
q
1 −λx
−λq
e
= −qe
−
λ
0
1
−λq
−λq
= −qe
+
1−e
λ
=
∞
Z
Z
Z
dx = q
∞
λe−λx dx = qe−λq
q
E min(X (ω), q) =
1
λ
1 − e−λq
12.22
WR 1
Beispiel 1
W. Merz
Mittlerer Gewinn als Funktion der Bestellmenge q:
g(q) = p2 E(min(X (ω), q)) − p1 q =
p2
1 − e−λq − p1 q
λ
Notwendige Bedingung für eine Extremalstelle:
g 0 (q) =
p2
λe−λq − p1 = p2 e−λq − p1 = 0
λ
p1
p2
q = λ1 ln pp12
e−λq =
=⇒
q ist Maximalstelle, denn g 00 (q) = −λp2 e−λq < 0
12.23
WR 1
Beispiel 2
W. Merz
X1 , X2 seien N (0, 1)-verteilte Zufallsvariable, Y = X12 + X22 .
Ohne zusätzliche Voraussetzungen kann die Verteilung von
X = (X1 , X2 ) nicht berechnet werden.
EY = E(X12 + X22 ) = E(X12 ) + E(X22 )
Xk2 = G(Xk ) mit G(t) = t 2
E(Xk2 )
Z
Z
G(t)P Xk (dt) = t 2 P Xk (dt) = m2 (P Xk )
Z
= m2 (N (0, 1)) = t 2 ϕ(t)dt = 1
=
EY = 2
12.24
WR 1
Die Varianz
W. Merz
X : Ω → R sei eine Zufallsvariable auf (Ω, A, P) mit der
Verteilung P X .
R
Erwartungswert: EX = m1 (P X ) = xP X (dx)
Zur Definition der Varianz einer Zufallsvariablen formen wir die
Varianz von P X um:
Z
Z
2
2
m̂2 (P X ) =
x − m1 (P X ) P X (dx) = (x − EX ) P X (dx)
Z
=
G(x)P X (dx)
mit G(x) = (x − EX )2 .
Z
Z
m̂2 (P X ) = G(x)P X (dx) = Y (ω)P(dω) = EY
mit Y (ω) = G(X (ω)) = (X (ω) − EX )2
m̂2 (P X ) = E(X − EX )2
12.25
WR 1
Die Varianz
W. Merz
Definition
Ist X : Ω → R eine Zufallsvariable auf einem
Wahrscheinlichkeitsraum (Ω, A, P) und existieren die
entsprechenden Erwartungswerte, so heißt
varP (X ) = EP (X − EP X )2
die Varianz der Zufallsvariablen X .
Kurzform: var(X ) = E(X − EX )2
12.26
WR 1
Die Ungleichung von Tschebyscheff
W. Merz
Theorem
P(|X − EX | > ε) ≤
var(X )
ε2
Beweis.
B = {ω ∈ Ω ; |X (ω) − EX | > ε} = (|X − EX | > ε)
Z (ω) = ε2 · 1B (ω) + 0 · 1B (ω)
R
EZ = Z dP = ε2 P(B) = ε2 P(|X − EX | > ε)
2
Z (ω) ≤ Y (ω) = (X (ω) − EX )
⇒
EZ ≤ EY
2
ε P(|X − EX | > ε) ≤ var(X )
12.27
WR 1
Rechenregeln
W. Merz
(1) var(X ) ≥ 0
Y (ω) = (X (ω) − EX )2 ≥ 0
⇒
var(X ) = EY ≥ 0
(2) var(X ) = 0 ⇒ X (ω) = EX P-f. ü.
Bn = {ω ∈ Ω ; |X (ω) − EX | > n1 }
0 ≤ P(Bn ) ≤ n2 var(X ) = 0
1
Ist |X (ω) − EX | > n1 , dann ist auch |X (ω) − EX | > n+1
, d.h.
Bn ⊂ Bn+1
S∞
B = n=1 Bn = {ω ∈ Ω ; |X (ω) − EX | > 0} = (|X − EX | > 0)
P(B) = limn→∞ P(Bn ) = 0
P(B) = P(X = EX ) = 1
12.28
WR 1
Rechenregeln
W. Merz
Algebraische Ausdrücke
2
(X (ω) − EX )2 = (X (ω)) − 2(EX ) · X (ω) + (EX )2
(X − EX )2 = X 2 − 2(EX ) · X + (EX )2
Algebraische Ausdrücke, in denen Zufallsvariablen
vorkommen, kann man mit den aus der Algebra gewohnten
Rechenregeln umformen.
(3) var(X ) = E(X 2 ) − (EX )2
Mit EX =: µ ist
E(X − EX )2
= E X 2 − 2µX + µ2
= E(X 2 ) − 2µEX + µ2
= E(X 2 ) − 2(EX )(EX ) + (EX )2
= E(X 2 ) − (EX )2
12.29
WR 1
Rechenregeln
W. Merz
2
(4) var(aX + b) = a var(X )
var(Y )
= E(Y − EY )2
2
= E [(aX + b) − E(aX + b)]
2
= E [aX + b − aEX − b]
2
= E [aX − aEX ]
= E a2 (X − EX )2
2
= a2 E (X − EX )
12.30
WR 1
Die Kovarianz
W. Merz
Definition
Für zwei Zufallsvariable X1 und X2 auf (Ω, A, P) heißt
cov(X1 , X2 ) = E [(X1 − EX1 )(X2 − EX2 )]
die Kovarianz von X1 und X2 .
(5) var(X1 + X2 ) = var(X1 ) + 2cov(X1 , X2 ) + var(X2 )
var(X1 + X2 )
2
= E [(X1 + X2 ) − E(X1 + X2 )]
=
=
+
+
2
E [(X1 − EX1 ) + (X2 − EX2 )]
E(X1 − EX1 )2
2E [(X1 − EX1 )(X2 − EX2 )]
E(X2 − EX2 )2
12.31
WR 1
Rechenregeln
W. Merz
(6) cov(X1 , X2 ) = E(X1 X2 ) − (EX1 )(EX2 )
cov(X1 , X2 )
=
=
=
=
E [(X1 − EX1 )(X2 − EX2 )]
E[X1 X2 − (EX1 )X2 − (EX2 )X1 + (EX1 )(EX2 )]
E(X1 X2 ) − (EX1 )EX2 − (EX2 )EX1 + (EX1 )(EX2 )
E(X1 X2 ) − (EX1 )(EX2 )
12.32
WR 1
Rechenregeln
W. Merz
(7) Stochastisch unabhängige Zufallsvariable
Sind X1 und X2 stochastisch unabhängig, so ist
E(X1 X2 ) = (EX1 )(EX2 )
und daher
cov(X1 , X2 ) = 0
sowie
var(X1 + X2 ) = var(X1 ) + var(X2 )
Achtung!
Die Umkehrung dieser Aussage ist nicht immer richtig! Aus
cov(X1 , X2 ) = 0 folgt normalerweise nicht, dass die beiden
Zufallsvariablen stochastisch unabhängig sind.
12.33
WR 1
Beispiel
W. Merz
Der Zufallsvektor X = (X1 , X2 ) sei auf
M = {(x1 , x2 ) ∈ R2 , |x1 | + |x2 | ≤ 1} uniform verteilt.
x2
6
@
@
@
@
@
@
@
@
@
x1
@
@
@
@
@
12.34
WR 1
Beispiel
√
M ist ein Quadrat mit der Kantenlänge 2 und der Fläche
|M| = 2. Die Verteilung P X des Zufallsvektors X besitzt daher
die Dichte
1
falls |x1 | + |x2 | ≤ 1
2
f (x1 , x2 ) =
0 sonst
W. Merz
Marginaldichten: Die Dichte f ist in den beiden Argumenten
symmetrisch: f (x1 , x2 ) = f (x2 , x1 ), Daher sind die beiden
Marginaldichten gleich.
Z ∞
f2 (t) = f1 (t) =
f (t, x2 )dx2
−∞
12.35
WR 1
Beispiel
W. Merz
6x2
@
@
@
@
1 − |x1 |
@
@
@
@
@
@
x1
@
@
−(1 − |x1 |)
@
@
@
@
@
@
12.36
WR 1
Beispiel
W. Merz
Für t < −1 oder t > 1 ist f (t, x2 ) = 0 für alle x2 , so dass
f2 (t) = f1 (t) = 0.
Für −1 ≤ t < 1 ist
Z
∞
Z
1−|t|
f (t, x2 )dx2 =
−∞
−(1−|t|)
1
dx2 = 1 − |t|
2
Erwartungswerte der Komponenten X1 und X2 :
Z
EX2 = EX1 =
Z
1
t(1 − |t|)dt = 0
tf1 (t)dt =
−1
12.37
WR 1
Beispiel
W. Merz
Kovarianz:
Z
cov(X1 , X2 ) = E(X1 X2 ) = x1 x2 P X (d(x1 , x2 ))
Z
Z
1
=
x1 x2 f (x1 , x2 )d(x1 , x2 ) =
x1 x2 d(x1 , x2 )
M 2
!
Z
Z 1−|x1 |
1 1
=
x1
x2 dx2 dx1
2 −1
−(1−|x1 |)
Z
1 1
=
x1 · 0dx1 = 0
2 −1
Die Zufallsvariablen X1 , X2 sind aber nicht stochastisch
unabhängig!
12.38
WR 1
Beispiel
W. Merz
Z.B. auf dem Dreieck
D = {(x1 , x2 ) ∈ R2 ; 0 < x1 < 1 , 1 − x1 < x2 < 1} ist
f (x1 , x2 ) = 0, während f1 (x1 )f2 (x2 ) = (1 − x1 )(1 − x2 ) > 0.
x2
6
@
@
D
@
@
@
@
@
@
@
x1
@
@
@
@
@
12.39
Rechenregeln
WR 1
W. Merz
(8) cov(Y , Y ) = var(Y )
cov(Y , Y ) = E[(Y − EY )(Y − EY )] = E(Y − EY )2 = var(Y )
(9) cov(X1 , X2 ) = cov(X2 , X1 )
E(X1 X2 ) − (EX1 )(EX2 ) = E(X2 X1 ) − (EX2 )(EX1 )
Anmerkung: Das gilt nur für reellwertige Zufallsvariable. Für komplexwertige ist
die Kovarianz anders definiert.
(10) cov(X1 + a, X2 + b) = cov(X1 , X2 )
cov(X1 + a, Y ) = E[((X1 + a) − E(X1 + a))(Y − EY )]
= E[(X1 + a − EX1 − a))(Y − EY )]
= E[(X1 − EX1 )(Y − EY )] = cov(X1 , Y )
12.40
Bilinearität
WR 1
W. Merz
(11) cov(a1 X1 + a2 X2 , Y ) = a1 cov(X1 , Y ) + a2 cov(X2 , Y )
=
=
=
=
=
=
cov(a1 X1 + a2 X2 , Y )
E[a1 X1 + a2 X2 − E(a1 X1 + a2 X2 )](Y − EY )
E(a1 X1 + a2 X2 − a1 EX1 − a2 EX2 )(Y − EY )
E[a1 (X1 − EX1 ) + a2 (X2 − EX2 )](Y − EY )
E[a1 (X1 − EX1 )(Y − EY ) + a2 (X2 − EX2 )(Y − EY )]
a1 E(X1 − EX1 )(Y − EY ) + a2 E(X2 − EX2 )(Y − EY )
a1 cov(X1 , Y ) + a2 cov(X2 , Y )
12.41
WR 1
Bilinearität
W. Merz
(12) cov(X , b1 Y1 + b2 Y2 ) = b1 cov(X , Y1 ) + b2 cov(X , Y2 )
cov(X , b1 Y1 + b2 Y2 )
= cov(b1 Y1 + b2 Y2 , X )
= b1 cov(Y1 , X ) + b2 cov(Y2 , X )
= b1 cov(X , Y1 ) + b2 cov(X , Y2 )
12.42
WR 1
Bilinearität
W. Merz
Allgemein:
cov
m
X
i=1
ai Xi ,
n
X
k =1
!
bk Yk
=
m X
n
X
ai bk cov(Xi , Yk ) = a> CXY b
i=1 k =1
wobei a> der Zeilenvektor mit den Komponenten ai ,
b der Spaltenvektor mit den Komponenten bk
und CXY die m × n-Matrix

cov(X1 , Y1 ) cov(X1 , Y2 ) . . . cov(X1 , Yn )
 cov(X2 , Y1 ) cov(X2 , Y2 ) . . . cov(X2 , Yn )


..
..
..
..

.
.
.
.
cov(Xm , Y1 ) cov(Xm , Y2 )





. . . cov(Xm , Yn )
12.43
WR 1
Bilinearität
W. Merz
Exercise
Die Zufallsvariablen X1 und X2 seien stochastisch unabhängig
und exponentiell verteilt mit Parametern λ1 = 1 bzw. λ2 = 2.
Welche Kovarianz besitzen die Zufallsvariablen
Y1 = 3X1 + 2X2 und Y2 = X1 − X2 ?
cov(Y1 , Y2 )
=
=
=
=
cov(3X1 + 2X2 , Y2 )
3cov(X1 , Y2 ) + 2cov(X2 , Y2 )
3cov(X1 , X1 − X2 ) + 2cov(X2 , X1 − X2 )
3cov(X1 , X1 ) − 3cov(X1 , X2 )
+2cov(X2 , X1 ) − 2cov(X2 , X2 )
X1 und X2 sind stochastisch unabhängig, daher
cov(X1 , X2 ) = cov(X2 , X1 ) = 0:
cov(Y1 , Y2 ) = 3cov(X1 , X1 ) − 2cov(X2 , X2 )
12.44
WR 1
Beispiel
W. Merz
cov(Y1 , Y2 ) = 3cov(X1 , X1 ) − 2cov(X2 , X2 )
cov(X , X ) = var(X ):
cov(Y1 , Y2 ) = 3var(X1 ) − 2var(X2 )
var(X ) = m̂2 (P X ):
cov(Y1 , Y2 ) = 3m̂2 (E(λ1 ))−2m̂2 (E(λ2 )) = 3
1
5
1
2
−2 2 = 3− =
2
4
2
λ1
λ2
12.45
WR 1
Die Kovarianzmatrix
W. Merz
Definition
Für einen Zufallsvektor X = (X1 , X2 , . . . , Xn ) heißt die Matrix


cov(X1 , X1 ) cov(X1 , X2 ) . . . cov(X1 , Xn )
 cov(X2 , X1 ) cov(X2 , X2 ) . . . cov(X2 , Xn ) 


CX = 

..
..
..
.
.


.
.
.
.
cov(Xn , X1 ) cov(Xn , X2 )
. . . cov(Xn , Xn )
die Kovarianzmatrix von X .
12.46
WR 1
Eigenschaften
W. Merz
CX ist symmetrisch
Folgt aus cov(Xi , Xk ) = cov(Xk , Xi )
CX ist positiv semidefinit
Ist a> = (a1 , a2 , . . . , an ) ein beliebiger reeller Zahlenvektor, so
besitzt die Zufallsvariable Y = a1 X1 + a2 X2 + . . . + an Xn die
Varianz
!
n
n
X
X
var(Y ) = cov(Y , Y ) = cov
ai Xi ,
ak Xk = a> CX a
i=1
k =1
Da Varianzen stets nichtnegativ sind, ist für beliebige Vektoren
a
a> CX a ≥ 0
12.47
Die Kovarianzmatrix
WR 1
W. Merz
Gibt es einen Vektor a 6= 0 mit a> CX a = 0, so besitzt die
Zufallsvariable Y = a1 X1 + . . . + an Xn die Varianz Null und ist
damit fast überall gleich einer Konstanten c bzw. sind die
Zufallsvariablen Xi fast überall affin linear abhängig.
12.48
WR 1
Cauchy-Schwarzsche Ungleichung
W. Merz
Theorem
|cov(X1 , X2 )| ≤
p
p
var(X1 ) var(X2 )
wobei die linke und rechte Seite genau dann gleich sind, wenn
es Konstanten a, b und c mit a2 + b2 > 0 gibt, so dass
aX1 (ω) + bX2 (ω) = c
P-fast überall
12.49
WR 1
Der Korrelationskoeffizient
W. Merz
Definition
Für positive Varianzen heißt
cov(X1 , X2 )
p
var(X1 ) var(X2 )
ρ(X1 , X2 ) = p
der Korrelationskoeffizient von X1 und X2 .
Aus der Cauchy-Schwarz-Ungleichung folgt, dass
−1 ≤ ρ(X1 , X2 ) ≤ 1
ρ(X1 , X2 ) = ±1 besagt, dass X1 und X2 affin linear abhängig
sind.
Ist ρ(X1 , X2 ) = 0 so heißen X1 und X2 unkorreliert.
12.50