Im rechtwinkligen Dreieck gilt der Satz von Thales. Zeichne einen

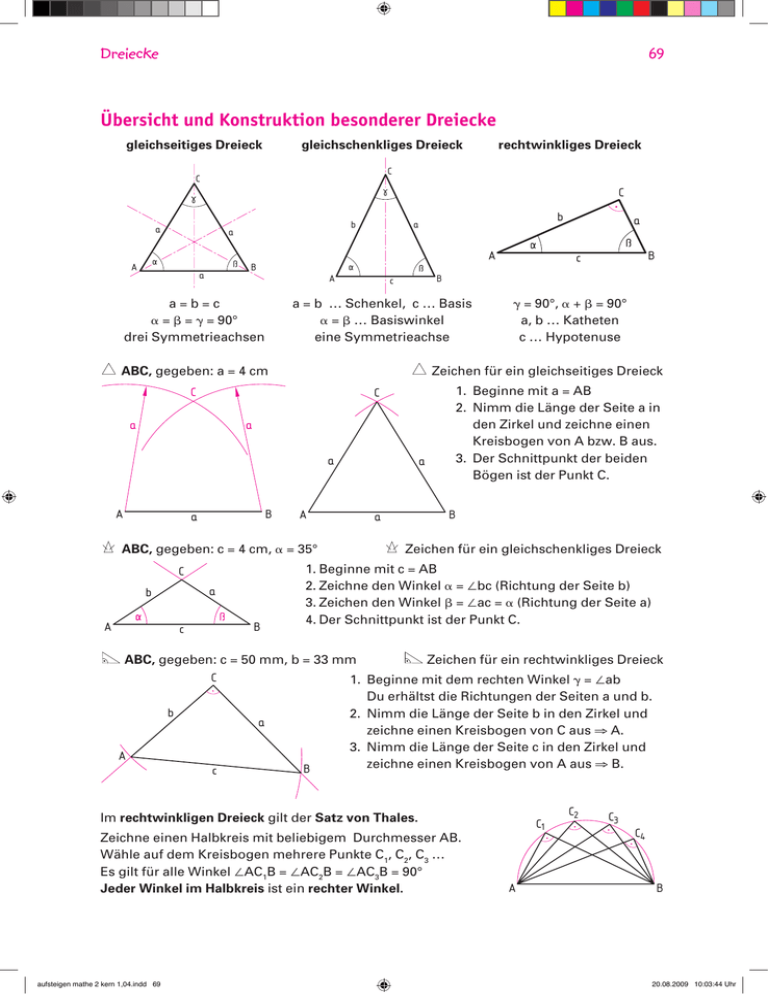
Dreiecke
69
Übersicht und Konstruktion besonderer Dreiecke
gleichseitiges Dreieck
gleichschenkliges Dreieck
rechtwinkliges Dreieck
C
C
C
a
A
b
a
b
a
A
B
a
A
a = b = c
a = b = g = 90°
drei Symmetrieachsen
.
.
ABC,
gegeben: a = 4 cm a
.
B
a
A
a
C
a
b
A
B
c
B
a
.
ABC, gegeben: c = .4 cm, a = 35° .
1. Beginne mit a = AB
2. Nimm die Länge der Seite a in
den Zirkel und zeichne einen
Kreis­bogen von A bzw. B aus.
3. Der Schnittpunkt der beiden
Bögen ist der Punkt C.
a
A
g = 90°, a + b = 90°
a, b … Katheten
c … Hypotenuse
.
. Dreieck
Zeichen
für ein gleichseitiges
C
a
B
c
B
c
a = b … Schenkel, c … Basis
a = b … Basiswinkel
eine Symmetrieachse
C
a
.
Zeichen für ein gleichschenkliges
Dreieck
1.Beginne mit c = AB
2.Zeichne den Winkel a = ∠bc (Richtung der Seite b)
3.Zeichen den Winkel b = ∠ac = a (Richtung der Seite a)
4.Der Schnittpunkt ist der Punkt C.
.
.
ABC, gegeben: c = 50 mm,
b = 33 mm . Zeichen für ein rechtwinkliges
Dreieck
C
1. Beginne mit dem rechten Winkel g = ∠ab
b
a
A
c
B
Du erhältst die Richtungen der Seiten a und b.
2. Nimm die Länge der Seite b in den Zirkel und
zeichne einen Kreisbogen von C aus ⇒ A.
3. Nimm die Länge der Seite c in den Zirkel und
zeichne einen Kreisbogen von A aus ⇒ B.
Im rechtwinkligen Dreieck gilt der Satz von Thales.
Zeichne einen Halbkreis mit beliebigem Durchmesser AB.
Wähle auf dem Kreisbogen mehrere Punkte C1, C2, C3 …
Es gilt für alle Winkel ∠AC1B = ∠AC2B = ∠AC3B = 90°
Jeder Winkel im Halbkreis ist ein rechter Winkel.
aufsteigen mathe 2 kern 1,04.indd 69
C1
A
C2
C3
C4
B
20.08.2009 10:03:44 Uhr