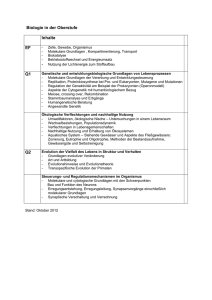
x = i
Werbung

Verfahren zu Strukturvorhersagen in vereinfachten Modellen Tobias Voigt Sommerakademie 2002 St. Johann Einführung ! Sequenzierung von Proteinen und Nukleinsäuren ist heute Routine ! Die räumliche Struktur dieser Biopolymere ist zunächst unbekannt ! Aber: Die Struktur ist der Schlüssel zur Funktionsweise ! ! ! September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 2 Möglichkeit 1: Röngtenstrukturanalyse ! Das Beugungsbild eines ProteinEinkristalls wird aufgenommen ! Vorteil: hohe Genauigkeit ! Aber: Es werden Kristalle einer Größe von ≈1 mm benötigt " schwierig oder gar nicht zu erhalten September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 3 Möglichkeit 2: NMR-Spektroskopie ! Vorteil: Biomoleküle können in wässriger Lösung vermessen werden ! Nachteil: Sehr aufwendige Spektrenauswertung ! September 2002 Hoher apparativer Aufwand Tobias Voigt, MPI für molekulare Physiologie, Dortmund 4 Beispiel: 900 MHz NMR September 2002 Tobiasnicht Voigt, Leider amMPI MPIfür für molekulare Physiologie, Dortmund 5 Vorhersagemöglichkeiten? ! Die Struktur wird allein durch die Sequenz bestimmt ! Synthetisch hergestellte Proteine nehmen von selbst die richtige Struktur an " Die spontane Faltung stellt ein (lokales) Energieminimum dar September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 6 Das HP-Modell ! Um das Minimum sicher zu finden, sind Vereinfachungen nötig September 2002 # Nur die Position der Aminosäure als Ganzes wird betrachtet # Die Aminosäure darf sich nur auf bestimmten Gitterplätzen befinden Tobias Voigt, MPI für molekulare Physiologie, Dortmund 7 Das HP-Modell ! Die Anzahl der unterschiedlichen Aminosäuren wird von 20 auf 2, nämlich „H“ und „P“ reduziert September 2002 # H = hydrophob (Gly, Ala, Val, Leu, Ile, Phe, Pro, Met) # P = polar (Arg, Asn, Asp, Cys, Gln, Glu, His, Lys, Ser, Thr, Trp, Tyr) Tobias Voigt, MPI für molekulare Physiologie, Dortmund 8 Was ist die treibende Kraft? ! Polare Gruppen gehen Wasserstoffbrückenbindungen mit andern polaren Gruppen oder Wasser ein ! Unpolare Gruppen stören diese WW, daher treten auch diese miteinander in direkten Kontakt " „hydrophober Kollaps“ September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 9 Das HP-Modell – Energie ! Befinden sich zwei H-Aminosäuren in unmittelbaren Kontakt #" ! Alle anderen Kontakte #" September 2002 Energie = -1 Energie = 0 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 10 Faltung im quadratischen Gitter 2 HH-Kontakte " Energie = -2 September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 11 Obere Grenze für HH-Kontakte ! Es existieren bereits Approximations-Algorithmen und heuristische Verfahren ! Aber: Diese liefern nicht unbedingt die Konformation mit der niedrigsten Energie September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 12 Modell mit zwei Ebenen ! 5 Kontakte in Ebene x = 1 ! 4 Kontakte in Ebene x = 2 ! 4 Kontakte zwischen den Ebenen September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 13 Berechnung der Kontakte ! Max. Anzahl der Kontakte zwischen Ebenen = min (n1,n2) ! Max. Anzahl der Kontakte innerhalb von Ebenen = 2n – a – b a= n , b = n a September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 14 Nachteile des kubischen Gitters ! Bei einem Protein HPHPHP usw. können keine HH-Kontakte auftreten ! Bei einem kubischen Gitter ist die Raumerfüllung bei Kugeln nur ! September 2002 56 % - andere Gitter sind besser Tobias Voigt, MPI für molekulare Physiologie, Dortmund 15 Kubisch innenzentrierte Packung September 2002 ! BCC = body centered cubic ! Raumerfüllung 68 % Tobias Voigt, MPI für molekulare Physiologie, Dortmund 16 Kubisch flächenzentrierte Packung September 2002 ! FCC = face centered cubic ! Raumerfüllung von 74 % Tobias Voigt, MPI für molekulare Physiologie, Dortmund 17 Hexagonal dichteste Packung ! HCP = hexagonal closed packing ! Raumerfüllung 74 % hexagonal September 2002 kubisch Tobias Voigt, MPI für molekulare Physiologie, Dortmund 18 Anpassung / Vereinfachung des FCC Ursprüngliches FCC September 2002 Nach Rotation Tobias Voigt, MPI für molekulare Physiologie, Dortmund 19 x D3 = y z x y 3 ∈ Z und x + y + z ist gerade . z Definition des FCC ! ! Ursprünglich: x D3 = y z x 3 Z y ∈ und x + y + z ist gerade z Nach Rotation: x D3 ' = y z x 3 y ∈ und x ist gerade Z z â ! September 2002 Satz der Vektoren: x y + 0.5 z + 0.5 N D '3 x y 3 und x ist ungerade Z ∈ z 0 0 = ±1 , 0 â 0 ±1 Tobias Voigt, MPI für molekulare Physiologie, Dortmund ±1 ±0,5 ±0,5 20 x D3 = y z x y 3 ∈ Z und x + y + z ist gerade . z Ein möglichst kleiner Kern ist wichtig September 2002 ! Für die Struktur des Proteins lässt sich auf den hydrophoben Kern zurückführen. Dieser muss eine möglichst kleine Oberfläche besitzen. ! Durch diesen Kern wird dann die Sequenz gelegt. Tobias Voigt, MPI für molekulare Physiologie, Dortmund 21 Aufteilung der HH-Kontakte September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 22 Obere Schranke für Anzahl der 4er, 3er, 2er und 1er Punkte September 2002 ! Problem: Die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte in x = i + 1 hängt von der genauen Position der Aminosäuren in x = i ab. ! In allen 3 Beispielen ist ni = 8, ai = Höhe, bi = Breite ! Gesucht : Parameter, welche die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte bestimmen Tobias Voigt, MPI für molekulare Physiologie, Dortmund 23 Obere Schranke für Anzahl der 4er, 3er, 2er und 1er Punkte September 2002 ! Problem: Die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte in x = i + 1 hängt von der genauen Position der Aminosäuren in x = i ab. ! In allen 3 Beispielen ist ni = 8, ai = Höhe, bi = Breite ! Gesucht : Parameter, welche die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte bestimmen Tobias Voigt, MPI für molekulare Physiologie, Dortmund 24 Obere Schranke für Anzahl der 4er, 3er, 2er und 1er Punkte September 2002 ! Problem: Die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte in x = i + 1 hängt von der genauen Position der Aminosäuren in x = i ab. ! In allen 3 Beispielen ist ni = 8, ai = Höhe, bi = Breite ! Gesucht : Parameter, welche die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte bestimmen Tobias Voigt, MPI für molekulare Physiologie, Dortmund 25 Obere Schranke für Anzahl der 4er, 3er, 2er und 1er Punkte September 2002 ! Problem: Die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte in x = i + 1 hängt von der genauen Position der Aminosäuren in x = i ab. ! In allen 3 Beispielen ist ni = 8, ai = Höhe, bi = Breite ! Gesucht : Parameter, welche die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte bestimmen Tobias Voigt, MPI für molekulare Physiologie, Dortmund 26 Obere Schranke für Anzahl der 4er, 3er, 2er und 1er Punkte September 2002 ! Problem: Die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte in x = i + 1 hängt von der genauen Position der Aminosäuren in x = i ab. ! In allen 3 Beispielen ist ni = 8, ai = Höhe, bi = Breite ! Gesucht : Parameter, welche die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte bestimmen Tobias Voigt, MPI für molekulare Physiologie, Dortmund 27 Obere Schranke für Anzahl der 4er, 3er, 2er und 1er Punkte ! Problem: Die Anzahl der 4er-, 3er-, 2er- und 1er-Punkte in x = i + 1 hängt von der genauen Position der Aminosäuren in x = i ab. ! Lösung: Sei l die Anzahl der 3er-Punkte, dann gilt: Anzahl der 4er = ni + 1 – ai – bi Anzahl der 2er = 2ai + 2bi – 2l – 4 Anzahl der 1er = l + 4 Für l lässt sich eine obere Schranke angeben! September 2002 Tobias Voigt, MPI für molekulare Physiologie, Dortmund 28 Leistungsfähigkeit der Vorhersagen September 2002 ! Derzeit bis etwa 130 Aminosäuren in angemessener Rechenzeit. ! Berechnung auch via Internet möglich: ! http://www.bio.inf.uni-jena.de/Prediction/prediction.cgi Tobias Voigt, MPI für molekulare Physiologie, Dortmund 29