17 Bewegung geladener Teilchen im homogenen elektrischen

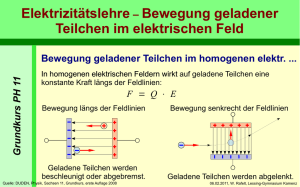
56 r Bewegung geladener Teilchen in elektrischen und magnetischen Feldern
17 Bewegung geladener Teilchen
im homogenen elektrischen Längsfeld
Mit elektrischen Längsfeldern kann man die kinetische Energie geladener Teilchen erhöhen oder verringern, ohne dabei die Bewegungsrichtung der Teilchen zu
ändern. Man findet diese Felder z. B. als Elektronenbeschleuniger in „Elektronenkanonen“ oder in Röntgenröhren. Als bremsende Gegenfelder eignen sie sich z. B.
für die experimentelle Untersuchung des Fotoeffekts ebenso wie für die Reichweitenbestimmung von Teilchen, die in der natürlichen radioaktiven Strahlung
vorkommen.
Sie wissen bereits, wie man die Bewegung eines Massenpunkts, der längs einer
Geraden die konstante Beschleunigung a erfährt, mathematisch beschreibt: Man
legt die Achse eines eindimensionalen Koordinatensystems so, dass sie mit der
Geraden zusammenfällt.
Bezeichnen
• x(t) bzw. x0 die orientierten Abstände des Massenpunkts vom Koordinatenursprung zum Zeitpunkt t bzw. zur Startzeit,
• v0 bzw. v(x) die orientierten Geschwindigkeiten am Anfang und am Ende der
Beschleunigungsstrecke,
• v(t) und v0 die orientierten Geschwindigkeiten zur Zeit t bzw. zur Startzeit,
so gelten die Bewegungsgesetze der Mechanik:
(1) v(t) = a ⋅ t + v 0
(2) x(t) = 12 a ⋅ t 2 + v 0 ⋅ t + x 0
(3) v(x) 2 − v(x 0 ) 2 = 2a ⋅ (x − x 0 )
Um diese auf geladene Teilchen übertragen zu können, berechnet man die Beschleunigung, die ein geladenes Teilchen in einem homogenen elektrischen
Längsfeld erfährt.
Regel
Beschleunigung im elektrischen Feld
Ein Teilchen der Masse m und der Ladung q erfährt in einem homogenen elektrischen Feld der Stärke E eine konstante Beschleunigung vom Betrag
a=
q
m
⋅ E.
Positiv geladene Teilchen werden in Feldlinienrichtung beschleunigt, negativ geladene entgegengesetzt dazu.
Bewegung geladener Teilchen im homogenen elektrischen Längsfeld r 57
Begründung: Wirkt auf einen Körper der Masse m eine ausschließlich den Bewegungszustand verändernde Kraft F, so erfährt er nach dem 2. Newton’schen Gesetz eine in die Richtung der Kraft wirkende Beschleunigung vom Betrag a so,
dass F = m ⋅ a. Weil die beschleunigende Kraft F hier die elektrische Kraft F = q ⋅ E
des Felds auf die Ladung q ist gilt:
q
m⋅a = q⋅E ⇔ a = m ⋅E
Die Bewegung geladener Teilchen in homogenen elektrischen Längsfelder unterliegt daher folgenden Gesetzen:
Regel
Bewegungsgesetze für geladene Teilchen im elektrischen Längsfeld
Ist die Anfangsgeschwindigkeit v 0 des Teilchens null oder parallel zu E und ist
das elektrische Feld homogen, so wird das Teilchen längs einer Geraden parallel
zu den Feldlinien konstant beschleunigt.
Befindet sich das Teilchen zum Zeitpunkt t = 0 s im Ursprung
einer Koordinatenachse, die parallel und in Richtung des Feldstärkevektors E verläuft, so gilt für
(1) seine Geschwindigkeit v(t) zum Zeitpunkt t:
v(t) =
q⋅E
⋅ t + v0
m
1. Bewegungsgesetz
(2) seine Entfernung vom Koordinatenursprung:
x(t) =
q⋅E 2
⋅ t + v0 ⋅ t + x0
2m
2. Bewegungsgesetz
(3) seine Geschwindigkeit v(x) am Ort x:
v(x) 2 − v(x 0 ) 2 =
2q ⋅ E
⋅ (x − x 0 )
m
3. Bewegungsgesetz
In diesen Formeln ist bei q das Ladungsvorzeichen zu berücksichtigen. Geschwindigkeiten sind positiv, wenn sich das Teilchen in Richtung des Feldstärkevektors
bewegt, andernfalls negativ.
Die möglichen Ausgangssituationen, in denen sich eine Ladung im homogenen
elektrischen Feld befinden kann, lassen sich gut mit den geradlinigen Würfen
vergleichen, denen ein Massepunkt im Schwerefeld unterliegen kann. Die Richtung der Feldkraft hängt dabei vom Vorzeichen der Ladung ab:
„freier Fall“
„senkrechter Wurf
nach unten“
„senkrechter Wurf
nach oben“