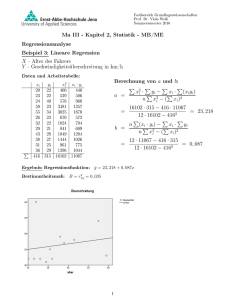
Beispiel 2: Gegeben ist folgende Häufigkeitsverteilung der

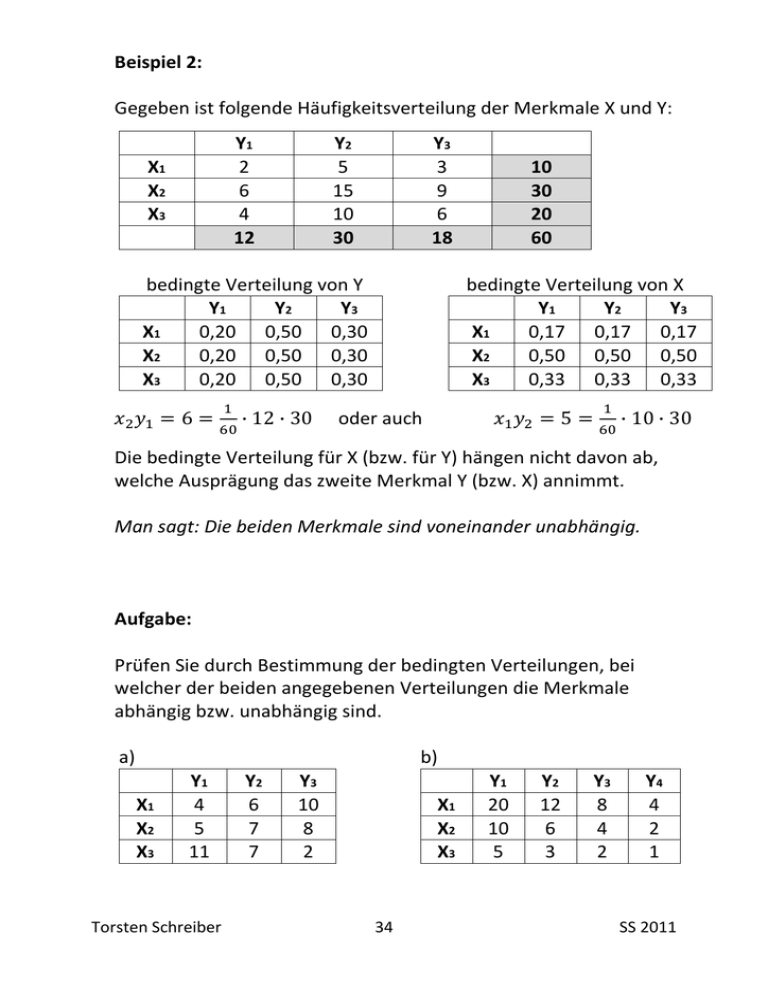
Beispiel 2:
Gegeben ist folgende Häufigkeitsverteilung der Merkmale X und Y:
Y1
2
6
4
12
X1
X2
X3
Y2
5
15
10
30
Y3
3
9
6
18
bedingte Verteilung von Y
Y1
Y2
Y3
X1
0,20 0,50 0,30
X2
0,20 0,50 0,30
X3
0,20 0,50 0,30
= 6 =
∙ 12 ∙ 30
10
30
20
60
bedingte Verteilung von X
Y1
Y2
Y3
X1
0,17 0,17 0,17
X2
0,50 0,50 0,50
X3
0,33 0,33 0,33
= 5 =
oder auch
∙ 10 ∙ 30
Die bedingte Verteilung für X (bzw. für Y) hängen nicht davon ab,
welche Ausprägung das zweite Merkmal Y (bzw. X) annimmt.
Man sagt: Die beiden Merkmale sind voneinander unabhängig.
Aufgabe:
Prüfen Sie durch Bestimmung der bedingten Verteilungen, bei
welcher der beiden angegebenen Verteilungen die Merkmale
abhängig bzw. unabhängig sind.
a)
b)
X1
X2
X3
Y1
4
5
11
Torsten Schreiber
Y2
6
7
7
Y3
10
8
2
X1
X2
X3
34
Y1
20
10
5
Y2
12
6
3
Y3
8
4
2
Y4
4
2
1
SS 2011
Regressionsfunktion für Zweidimensionalität
Es wird vorausgesetzt, dass bei einer zweidimensionalen Verteilung der
metrisch messbaren Merkmale X und Y, diese statistisch voneinander
abhängig sind.
Eine Funktion = (), die die Tendenz der Abhängigkeit dieser
Merkmale beschreibt, nennt man Regressionsfunktion.
y-x-Regressionsfunktion: Abhängigkeit vom Merkmal Y von X
x-y-Regressionsfunktion: Abhängigkeit vom Merkmal X von y
Als gängige Funktionen werden zumeist die auf Seite 27 genannten
Arten in der Praxis genutzt.
(Gerade, Parabel, Exponential-, Logarithmus bzw. Potenzfunktion)
Kriterium der kleinsten Quadrate (KQ-Kriterium):
Die Koeffizienten einer Regressionsfunktion der Form = () zur
Tendenzbeschreibung der Merkmale X und Y werden so bestimmt,
dass die Summe der quadrierten Abweichungen der Beobachtungswerte von den zugehörigen Funktionswerten ein Minimum wird.
( − ) = ( ) !
Die somit bestimmte Funktion wird KQ-Regressionsfunktion genannt
Grafische Interpretation der Differenzen:
Torsten Schreiber
35
SS 2011
Lineare Regressionsfunktion:
Existiert zwischen den Merkmalen X und Y statistische Abhängigkeit
und wird als Funktion die Form = " ∙ + $ gewählt werden die
Koeffizienten a und b wie folgt bestimmt:
"=
∑ − ∑ ∑ ∑ − &∑ '
bzw. mittels Varianz
"=
()*(+, -)
./
und
$=
∑ ∑ − ∑ ∑ ∑ − &∑ '
bzw. mittels Varianz
$=
∑ ∙ 01 −
∑ ./
∙ 0/
Zur Bestimmung der Regressionskoeffizienten berechnet man die
benötigten Summe am besten mittels einer Hilfstabelle, in der
Ausprägungen von X und Y verrechnet werden.
Für eine lineare Regressionsfunktion der Form = " ∙ + $ mit den
Mittelwerten 0/ und 01 gilt stets 01 = " ∙ 0/ + $, d.h. der Punkt
(0/ ; 01 ) muss auf der Geraden liegen.
Torsten Schreiber
36
SS 2011
Beispiel:
Gegeben sind die folgenden Beobachtungswerte ( ; )
(1;2), (2;3), (3;5), (4;4), (4;6), (5;4), (6;8), (7;7), (9;8).
0/ ≈ 4,6 ! 01 ≈ 5,2
Summen-Hilfstabelle:
xi
yi
xi²
yi²
xi yi
56 − 75
86 − 78
Produkt
1
2
1
4
2
-3,6
-3,2
11,5
2
3
4
9
6
-2,6
-2,2
5,7
3
5
9
25
15
-1,6
-0,2
0,3
4
4
16
16
16
-0,6
-1,2
0,7
4
6
16
36
24
-0,6
0,8
-0,4
5
4
25
16
20
0,4
-1,2
-0,5
6
8
36
64
48
1,4
2,8
4,0
7
7
49
49
49
2,4
1,8
4,3
9
8
81
64
72
4,4
2,8
12,3
Berechnung mittels Variante 1:
"=
∑ − ∑ ∑ 9 ∙ 252 − 41 ∙ 47
=
= 0,7544
∑ − (∑ )
9 ∙ 237 − 41
und
∑ ∑ − ∑ ∑ 237 ∙ 47 − 41 ∙ 252
$=
=
= 1,7845
∑ − (∑ )
9 ∙ 237 − 41
Berechnung mittels Variante 2:
"=
()*(+, -) 4,21
37,89
=
=
0,754
()*(+;
-)
=
./
5,58
9
und
$=
∑ ∙ 01 −
∑ ./
∙ 0/
237 47 252 41
∙
−
∙
9
9
9
9 = 1,785
=
5,58
1
41 . = ∙ 237 − < = = 5,58
9
9
Torsten Schreiber
37
SS 2011
41
47
237
283
252
37,89
Graph zur Regressionsgeraden: = 0,7544 ∙ + 1,7845
Aufgabe 1:
Gegeben sind folgende Wertepaare der Merkmale X und Y.
(1;2), (1;4), (2;4), (3;3), (3;5), (4;6), (5;4), (6;5), (7;9), (8;8)
a) Weisen Sie nach, dass die Merkmale X und Y abhängig sind.
b) Bestimmen Sie das arithmetische Mittel zu X und Y.
c) Berechnen Sie die Varianz als auch Kovarianz der Verteilung.
d) Berechnen Sie die lineare KQ-Regressionsfunktion mittels
Variante 1 (KQ-Kriterium)
Variante 2 (Varianz / Kovarianz)
Torsten Schreiber
38
SS 2011