Wirtschaftsstatistik - Fachhochschule Dortmund

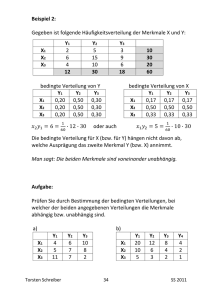
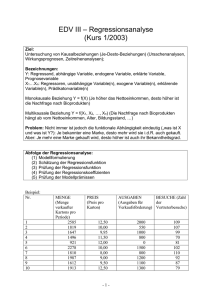
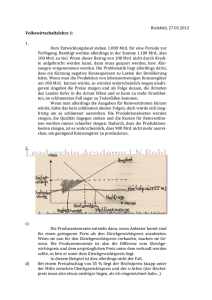
Fachhochschule Dortmund
Wintersemester 12/13
Fachbereich Wirtschaft
Prof. Dr. Laufner
Studiengänge BA Betriebswirtschaft und BA International Business (Management)
Übungsaufgaben
zur Woche
Modul 14 (BA Bw) bzw. Modul 3 (BA IB)
bzw. Modul 4 (BA IBM):
Wirtschaftsstatistik
Teil 1: Beschreibende Statistik
3. + 4. 12. 12
Aufgabe 10.1:
Für ein Produktionsunternehmen sind in der folgenden Tabelle die Produktionsmengen und die
Kosten für die vier ersten Monate eines Jahres angegeben.
Monate
Produzierte Menge (in Mio. Stück)
Produktionskosten (Mio €)
Jan.
5
8
Febr.
3
4
März
2
6
April
4
5
a) Berechnen Sie eine lineare Regressionsfunktion K̂ = K̂( x ) = a + b ⋅ x , die den Zusammenhang
zwischen produzierter Menge und Kosten möglichst gut charakterisiert.
(x produzierte Menge in Mio. Stück und K Kosten in Mio €)
Berechnungstabelle
Summe
Regressionsfunktion K̂ = K̂( x ) = a + b ⋅ x =
b) Zeichnen Sie das Streuungsdiagramm und die Regressionsfunktion in das folgende
Koordinatensystem ein. (Beschriftung der Achsen nicht vergessen!)
c) Interpretieren Sie die beiden Regressionskoeffizienten der berechneten Regressionsfunktion K̂ = K̂( x ) = a + b ⋅ x betriebswirtschaftlich:
a:
b:
Wie nennt man eine solche Funktion in der Betriebswirtschaftslehre?
d) Erstellen Sie auf der Basis der in a) ermittelten Regressionsfunktion eine Kostenprognose für
den Monat Mai, in dem eine Produktionsmenge von 6 Mio. Stück geplant ist.
2
e) Berechnen Sie den Korrelationskoeffizienten und das Bestimmtheitsmaß zur obigen
Regressionsrechnung.
f)
Interpretieren Sie das Bestimmtheitsmaß.
g) Berechnen Sie die Varianz der Produktionsmengen, der Produktionskosten und der Regressionswerte (Formel (2) und Summen aus der Berechnungstabelle verwenden). Zeigen Sie an diesem
Beispiel, dass das Bestimmtheitsmaß angibt, welcher Anteil der Varianz der Produktionskosten
erklärt wird durch die Regressionsfunktion bzw. die Varianz der Produktionsmengen.
Aufgabe 10.2:
Die Marktforschungsabteilung eines Unternehmens will für ein neues Produkt die Abhängigkeit der
Absatzmenge X vom Preis P empirisch untersuchen. Dazu wird in 4 vergleichbar großen Testmärkten
unter sonst annähernd gleichen Rahmenbedingungen 8 Wochen lang jeweils ein unterschiedlicher
Preis gefordert. Die Ergebnisse dieses Tests stehen in der folgenden Tabelle:
Testmärkte
P: Preis pro Stück (€)
X: Absatzmenge in 8 Wochen (Stück)
A
1,90
5.000
B
2,10
4.000
C
1,50
8.000
D
2,50
3.000
= x (p) = a + b ⋅ p , die die Abhängigkeit
a) Berechnen Sie eine lineare Regressionsfunktion x
zwischen Preis und Absatzmenge möglichst gut charakterisiert.
(p Preis in € und x Absatzmenge in Stück)
Berechnungstabelle
Testmarkt
p
x
Summe
Regressionsfunktion
x = x (p) = a + b ⋅ p =
b) Zeichnen Sie das Streuungsdiagramm und die Regressionsfunktion in ein Koordinatensystem
ein. (Beschriftung der Achsen nicht vergessen!)
c) Interpretieren Sie die beiden Regressionskoeffizienten a und b der in a) berechneten
Regressionsfunktion betriebswirtschaftlich.
a:
b:
d) Berechnen Sie den Korrelationskoeffizienten und das Bestimmtheitsmaß zur obigen
Regressionsrechnung.
e) Interpretieren Sie das Bestimmtheitsmaß für diesen Fall.
f) Erstellen Sie auf der Basis der in a) ermittelten Regressionsfunktion eine Absatzmengen-Prognose
für einen Testmarkt XYZ, der den Testmärkten A, B, C und D entspricht.
Welche Absatzmenge ist dort in 8 Wochen zu erwarten bei einem Preis von € 1,70.
g) Was halten Sie von der Prognosegüte der in f) erstellten Prognose?
h) Berechnen Sie für die Daten die Varianz der empirisch ermittelten Absatzmengen und die Varianz
der dazugehörigen Regressionswerte (= entsprechende Absatzmengen auf der
Regressionsfunktion).
Was ergibt der Quotient „Varianz der Regressionswerte zur Varianz der Absatzmengen“?
3
Aufgabe 10.3:
a) Welche Vorüberlegungen muss man anstellen, bevor man eine Regressions- und
Korrelationsrechnung durchführt?
b) Nach welchem Kriterium wird die lineare Regressionsfunktion ermittelt?
c) Welche mathematische Rechnung wird dabei genutzt?
d) Worüber informiert die statistische Kennzahl Kovarianz?
e) Welche Werte kann der Korrelationskoeffizient annehmen?
f) Welcher Zusammenhang liegt vor, wenn der Korrelationskoeffizient die Intervallgrenzen des
Wertebereichs annimmt?
g) Worüber informiert der Kontingenzkoeffizient?
h) Welche Werte kann der Kontingenzkoeffizient annehmen?
Aufgabe 10.4:
Im Rahmen einer Marktforschungsstudie wurden 1000 Personen befragt, welches der beiden
Produkte Gamma und Delta sie bevorzugt kaufen.
Geschlecht Î
Markenwahl Ð
weiblich
männlich
Summe
Produkt Gamma
180
270
450
Produkt Delta
220
330
550
Summe
400
600
1000
Abbildung 1: Zweidimensionale Häufigkeitstabelle: Geschlecht und Markenwahl
Gibt es hier einen Zusammenhang zwischen Geschlecht und Markenwahl? Auf den ersten Blick nicht,
denn sowohl bei den Frauen als auch bei den Männern ist der Käuferanteil für Produkt Gamma 45%,
für Delta jeweils 55%.
Die Vertriebsleute zweifeln das Ergebnis an. Den Statistikern in der Marktforschungsabteilung
kommen Zweifel, ob eine zweidimensionale Analyse ausreicht. Daher nehmen sie als drittes Merkmal
das Alter (klassiert) hinzu.
Das Ergebnis einer dreidimensionalen Auszählung ist in Abbildung 2 dargestellt:
Alter Î
Geschlecht Î
Markenwahl Ð
bis unter 40 Jahre alt
40 Jahre und älter
Summe
weiblich
männlich
weiblich
Produkt Gamma
90
260
90
10
450
Produkt Delta
10
140
210
190
550
100
400
300
200
1000
Summe
männlich
Abbildung 2: Dreidimensionale Häufigkeitstabelle: Geschlecht, Alter und Markenwahl
a) Welche wesentliche Aussage steckt in der Tabelle in Abbildung 3?
b) Skizzieren Sie in einem Diagramm
- die möglichen,
- die zahlenmäßigen (Kontingenzkoeffizient C > 0) und die
- kausalen Zusammenhänge (Abhängigkeiten)
zwischen den drei Merkmalen Geschlecht, Alter und Markenwahl.
Aufgabe 10.5:
In Abbildung 3 sehen Sie ein Streuungsdiagramm, in dem jeweils der durchschnittliche Kartoffelverbrauch pro Kopf und Jahr in kg (K) und der Elektroenergieverbrauch in deutschen Haushalten in
Mrd. kWh pro Jahr (E) für 23 Jahre eingetragen sind.
4
Energie-Sparen durch höheren
Kartoffel-Verbrauch ?
120
120 Mrd. kWh
100
100 Mrd. kWh
80
80 Mrd. kWh
60
60 Mrd. kWh
40
40 Mrd. kWh
20
20 Mrd. kWh
0
60kg
0 Mrd. kWh
70kg
80kg
90kg
100kg
110kg
120kg
Die Daten stammen aus: Statistische Jahrbücher der Bundesrepublik Deutschland 1968 - 1990
Abbildung 3
Eine Regressions- und Korrelationsrechnung ergab die folgende lineare Regressionsfunktion:
Ê = 207.929 − 1.528,41⋅ K
und den folgenden Korrelationskoeffizienten (Bestimmtheitsmaß)
2
r = -0,965 (r = 0,931)
a) Energiepolitiker wollen die berechnete durchschnittliche Abhängigkeit zwischen Energie- und
Kartoffelverbrauch nutzen. Sie planen durch gezielte Werbemaßnahmen den durchschnittlichen
Kartoffelverbrauch in Deutschland pro Kopf und Jahr auf 150 kg zu erhöhen.
Erstellen Sie auf der Basis der Regressionsanalyse für diesen Fall eine bedingte Prognose für den
Elektroenergieverbrauch in deutschen Haushalten.
b) Was halten Sie von der obigen Regressions- und Korrelationsanalyse sowie der darauf
basierenden bedingten Prognose?
c) Machen Sie sich an diesem Beispiel den Unterschied zwischen Kausalität und Korrelation (d.h.,
hoher Korrelationskoeffizient) klar.
d) Wie lässt sich die hohe Korrelation erklären?