Aufgabenblatt 1

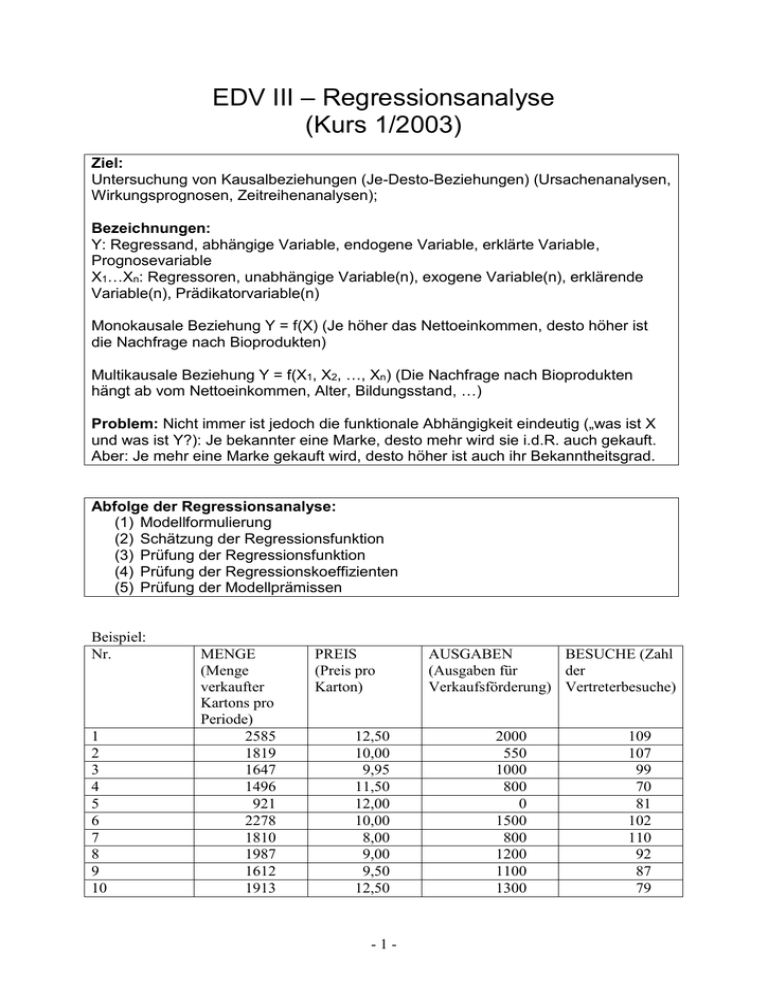
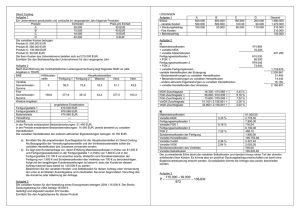
EDV III – Regressionsanalyse
(Kurs 1/2003)
Ziel:
Untersuchung von Kausalbeziehungen (Je-Desto-Beziehungen) (Ursachenanalysen,
Wirkungsprognosen, Zeitreihenanalysen);
Bezeichnungen:
Y: Regressand, abhängige Variable, endogene Variable, erklärte Variable,
Prognosevariable
X1…Xn: Regressoren, unabhängige Variable(n), exogene Variable(n), erklärende
Variable(n), Prädikatorvariable(n)
Monokausale Beziehung Y = f(X) (Je höher das Nettoeinkommen, desto höher ist
die Nachfrage nach Bioprodukten)
Multikausale Beziehung Y = f(X1, X2, …, Xn) (Die Nachfrage nach Bioprodukten
hängt ab vom Nettoeinkommen, Alter, Bildungsstand, …)
Problem: Nicht immer ist jedoch die funktionale Abhängigkeit eindeutig („was ist X
und was ist Y?): Je bekannter eine Marke, desto mehr wird sie i.d.R. auch gekauft.
Aber: Je mehr eine Marke gekauft wird, desto höher ist auch ihr Bekanntheitsgrad.
Abfolge der Regressionsanalyse:
(1) Modellformulierung
(2) Schätzung der Regressionsfunktion
(3) Prüfung der Regressionsfunktion
(4) Prüfung der Regressionskoeffizienten
(5) Prüfung der Modellprämissen
Beispiel:
Nr.
1
2
3
4
5
6
7
8
9
10
MENGE
(Menge
verkaufter
Kartons pro
Periode)
2585
1819
1647
1496
921
2278
1810
1987
1612
1913
PREIS
(Preis pro
Karton)
12,50
10,00
9,95
11,50
12,00
10,00
8,00
9,00
9,50
12,50
-1-
AUSGABEN
BESUCHE (Zahl
(Ausgaben für
der
Verkaufsförderung) Vertreterbesuche)
2000
550
1000
800
0
1500
800
1200
1100
1300
109
107
99
70
81
102
110
92
87
79
Menge Kartons
Aufgabe 1:
Erfassen Sie die Werte des Beispiels in SPSS. Vergeben Sie für die Variablen
aussagekräftige Namen und erfassen Sie die Variablenlabels
(1) Arbeiten zum Schritt „Modellformulierung“
Aufgabe 2:
Erstellen Sie ein Streudiagramm (Menüfolge: Grafiken -> Streudiagramm; Optionen:
Einfach -> Definieren). Es soll die Absatzmenge der Kartons in Abhängigkeit von der
Zahl der Vertreterbesuche dargestellt werden. Übernehmen Sie die geeigneten
Variablen in die Felder X- und Y-Achse.
Welcher Zusammenhang zwischen beiden Variablen ist zu vermuten?
Diagramm
Streudiagram m Absatzmenge - Vertreterbesuche
3000
2000
1000
0
60
70
80
90
100
110
120
V ertreterbes uc he
(2) Arbeiten zum Schritt „Schätzung der
Regressionsfunktion“
Aufgabe 3:
Ermitteln Sie die Regressionsfunktion
(Menüfolge: Analysieren -> Regression -> Linear; Optionen: Einfach -> Definieren).
Es soll die Absatzmenge der Kartons in Abhängigkeit von der Zahl der
Vertreterbesuche dargestellt werden. Übernehmen Sie die geeigneten Variablen in
die Felder „abhängige“ bzw. „unabhängige“ Variable.
-2-
Menge Kartons
3000
2000
1000
Beobachtet
0
Linear
60
70
80
90
100
110
120
Vertreterbesuche
(3) Arbeiten zum Schritt „Prüfung der
Regressionsfunktion“
a) Globale Prüfung der Regressionsfunktion
Bestimmtheitsmaß R2
F-Statistik
Standardfehler
b) Prüfung der Regressionskoeffizienten
t-Wert
Vertrauensintervall
Bestimmtheitsmaß:
Mißt die Güte der Anpassung der Regressionsfunktion an die empirischen Daten.
Das Bestimmtheitsmaß in dem Beispiel beträgt 0,346, d.h., dass 34,6% der
gesamten Abweichungen der beobachteten y-Werte (Verkaufte Kartons) von den
geschätzten Werten der Regressionsgleichung erklärt werden können. (erklärt
werden kann die Differenz jedes geschätzten ŷi zum Mittelwert). 65,4 % bleiben
unerklärt. Die Schwankungen der Absatzmenge Y sind zu einem wesentlichen Teil
durch andere Einflüsse als die Vertreterbesuche bedingt.
-3-
F-Test:
Soll die Frage beantworten, ob die Regression nicht nur deskriptiv für die Daten der
Stichprobe gilt, sondern ob die Regressionsfunktion als geschätztes Modell auch
Gültigkeit für die Grundgesamtheit hat.
Wenn zwischen der abhängigen Variablen Y und der/den unabhängigen Variable(n)
ein kausaler Zusammenhang besteht, so müssen die wahren
Regressionskoeffizienten βj ungleich Null sein.
Zur Prüfung des Modells wird die Gegenhypothese H0 („Nullhypothese“) aufgestellt.
Sie lautet: Es besteht kein Zusammenhang und somit haben die
Regressionskoeffizienten in der Grundgesamtheit alle den Wert Null.
(Anmerkung: Je weniger Beobachtungswerte, umso besser wird i.d.R. das
Bestimmtheitsmaß. Mit wenigen Beobachtungen kann man jedoch tendenziell nur
ein schlechteres Modell für die Grundgesamtheit erzielen)
Standardfehler der Schätzung:
Welcher mittlere Fehler wird bei Verwendung der Regressionsfunktion zur
Schätzung der abhängigen Variablen Y gemacht?
(4) Arbeiten zum Schritt „Prüfung der
Regressionskoeffizienten“


t-Test
Wenn der F-Test ergeben hat, dass nicht alle Regressionskoeffizienten βj
gleich Null sind, sind die Regressionskoeffizienten einzeln zu prüfen – mit der
Nullhypothese
H0: βj = 0
Ermittlung des Konfidenzintervalls der (wahren) Regressionskoeffizienten
(5) Arbeiten zum Schritt „Prüfung der Modellprämissen“





Linearität – Nichtlinearität ? (Streudiagramm)
Heteroskedastizität der Residuen? Im Dialogfeld „Diagramme“ der
Regressionsanalyse: für Y die Variable *ZRESID aufnehmen und als XVariable *ZPRED aufnehmen. Streudiagramm zeigt, keine
Heteroskedastizität
Autokorrelation
Durbin/Watson-Koeffizient d (= Indexwert für die Prüfung der Autokorrelation):
Der Durbin/Watson-Test prüft die Nullhypothese, dass die
Beobachtungswerte nicht autokorreliert sind. Hierzu wird ein empirischer Wert
d ermittelt, der die Differenz zwischen den Residuen von
aufeinanderfolgenden Beobachtungswerten aggregiert.
Wenn die Residuen zweier folgender Beobachtungswerte nahezu gleich sind
(d.h. sie unterliegen einem Trend – positive Autokorrelation), dann ist auch
der Wert von d klein.
Starke Sprünge in den Residuen führen zu hohen Werten von d. Dies deutet
auf eine negative Autokorrelation hin
Multikollinearität (bei mehreren Regressoren): Die Regressoren dürfen nicht
(exakt) linear voneinander abhängig sein.
Zur Aufdeckung von Multikollinearität kann eine Regression jeder
unabhängigen Variablen auf die übrigen unabhängigen Variablen
-4-
durchgeführt werden. Ein Wert Rj2 = 1 besagt dann, dass sich die Variable Xj
durch Linearkombination der anderen unabhängigen Variablen erzeugen
lässt und somit überflüssig ist (in abgeschwächter Form gilt dies für Rj2 nahe
1).
Verwandtes Maß: Toleranz Tj der Variablen Xj
Tj = 1-Rj2
kehrwert der Toleranz ist der Variance Inflation Factor VIF.
Aufgabe 4:
Führen Sie nun eine multivariate Regressionsanalyse [Blockweise Regression
(=Methode „Einschluß“)] mit den Beispielsdaten durch.
-5-