Approximationsalgorithmen am Beispiel des Traveling Salesman

Approximationsalgorithmen am Beispiel des
Traveling Salesman Problem
Seminararbeit
im Rahmen des Seminars „Algorithmentechnik“
vorgelegt von Leonie Sautter
Leiter des Seminars:
Juniorprof. Dr. Henning Meyerhenke
Institut für Theoretische Informatik
Karlsruher Institut für Technologie (KIT)
Karlsruhe, den 19. Juli 2012
Inhaltsverzeichnis
1 Einleitung
1
2 Grundlagen
2
2.1
Optimierungsprobleme . . . . . . . . . . . . . . . . . . . . . .
2
2.2
Approximationsalgorithmen . . . . . . . . . . . . . . . . . . .
2
2.3
Gütegarantien . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
3 Das Traveling Salesman Problem
5
4 Das metrische Traveling Salesman Problem
6
4.1
Einfüge-Heuristiken . . . . . . . . . . . . . . . . . . . . . . . .
6
4.2
Der Algorithmus von Christofides . . . . . . . . . . . . . . . .
8
5 Das geometrische Traveling Salesman Problem
11
5.1
Idee des Algorithmus . . . . . . . . . . . . . . . . . . . . . . .
12
5.2
Rundung
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
5.3
Partitionierung . . . . . . . . . . . . . . . . . . . . . . . . . .
13
5.4
Portale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
5.5
Der Algorithmus . . . . . . . . . . . . . . . . . . . . . . . . .
15
5.6
Analyse der Gütegarantie . . . . . . . . . . . . . . . . . . . .
16
1
Einleitung
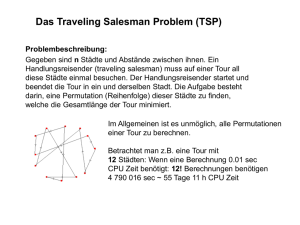
Das Problem des Handlungsreisenden (auf englisch das Traveling Salesman
Problem, kurz TSP) ist eines der bekanntesten kombinatorischen Optimierungsprobleme. Die Ausgangssituation ist dabei, dass ein Händler eine Rundreise durch eine bestimmte Anzahl an Städten machen möchte, um dort seine
Waren anzupreisen. Dabei möchte er am Ende wieder in seiner Heimatstadt
ankommen und insgesamt nur eine möglichst kurze Strecke zurücklegen.
Formalisieren kann man das Problem, indem man die Städte als Knoten eines
vollständigen, gewichteten Graphen versteht, wobei die Kantengewichte die
Entfernungen zwischen je zwei Städten widerspiegeln. Dann ist das Problem,
eine kürzeste Rundtour zu finden, gleich dem Problem, in diesem Graphen
einen Hamiltonkreis minimalen Gewichts zu finden. Ein Hamiltonkreis ist
dabei ein geschlossener Pfad, der alle Knoten des Graphen genau einmal
enthält.
Wie bereits 1972 gezeigt wurde, ist TSP NP-schwer1 . Damit gibt es, falls P 6=
NP gilt, keinen Algorithmus, der das Problem in polynomieller Laufzeit löst.
Dadurch sind sehr große Instanzen des TSP mit Computern in der Praxis
nicht mehr lösbar. In der Konsequenz sucht man daher nach Algorithmen,
die in einer möglichst geringen polynomiellen Laufzeit gute Approximationen
für eine kürzeste Rundtour liefern.
Im nächsten Kapitel werden die Anforderungen an solche Algorithmen formalisiert und es werden Möglichkeiten gezeigt, wie man die Qualität der
Algorithmen in Verhältnis setzen und vergleichen kann. Dabei wird sich vor
allem an den Kapiteln 1 bis 3 des Buches „Approximationsalgorithmen: Eine
Einführung“ von Rolf Wanka [12] orientiert.
Im dritten Kapitel wird dann genauer auf das allgemeine TSP eingegangen
und gezeigt, dass es weder mit absoluter noch mit relativer Gütegarantie in
polynomieller Zeit approximiert werden kann.
Daher wird sich in Kapitel 4 auf einen Spezialfall beschränkt. Für das metrische TSP wird zuerst eine Familie von sehr intuitiven Approximationsalgorithmen vorgestellt und ein erster Beweis für eine relative Gütegarantie
angegeben. Danach wird mit dem Algorithmus von Christofides der beste
bisher bekannte Approximationsalgorithmus für metrisches TSP beschrieben
und die relative Gütegarantie von 3/2 gezeigt.
In Kapitel 5 wird auf ein weiteres Unterproblem des TSP, das geometrische
TSP, eingegangen. Für dieses Problem ist es gelungen einen Approximati1
Dies ergibt sich direkt aus dem Resultat, dass das Hamiltonkreis-Problem NPvollständig ist [9]
1
onsalgorithmus zu finden, der es mit einem beliebig kleinen relativen Fehler
approximiert. Die Laufzeit hängt dabei von der oberen Schranke, die man
für den relativen Fehler wählt ab. Geht diese Schranke gegen 0 so wird die
Laufzeit exponentiell. Beschrieben wird die Variante, die der Erfinder des Algorithmus Sanjeev Arora in Kapitel 5 des Buches „The Traveling Salesman
Problem and Its Variations“ [2] selbst vorstellt.
2
Grundlagen
2.1
Optimierungsprobleme
Das Traveling Salesman Problem in seiner allgemeinen Formulierung, einen
Hamiltonkreis minimalen Gewichts in einem vollständigen Graphen zu finden, ist ein Optimierungsproblem. Es wird die Bewertungsfunktion, die einem Pfad sein Gewicht zuordnet, für alle zulässigen Pfade minimiert. Zulässig sind Pfade dabei dann, wenn sie geschlossen sind und jeden Knoten des
Graphen genau einmal durchlaufen. Verallgemeinert man dies kommt man
zu der folgenden Definition:
Definition 2.1 Ein kombinatorisches Optimierungsproblem Π besteht aus
vier Teilen:
• D die Menge der Probleminstanzen
• S(I) für I ∈ D die Menge der zulässigen Lösungen zu I
• f : S(I) → N+ die Bewertungsfunktion
• ziel ∈ {min, max}
Ein Entscheidungsproblem hingegen ist das Problem, für eine Instanz zu
entscheiden, ob sie zu einer bestimmten Sprache gehört. Im Fall des TSP
hat das zugehörige Entscheidungsproblem einen Parameter K an Stelle von
ziel. Das Problem ist dann zu entscheiden, ob es zu einer bestimmten Instanz
einen Hamiltonkreis mit einem Gewicht von höchstens K gibt.
2.2
Approximationsalgorithmen
Da das TSP NP-schwer ist, lässt sich kein polynomieller Algorithmus für das
Problem angeben, falls P 6= NP gilt. Da man in der Praxis aber trotzdem
möglichst schnell Lösungen finden möchte, muss man sich mit Näherungen
zufrieden geben.
2
Definition 2.2 Sei Π ein kombinatorisches Optimierungsproblem. Ein t(n)Zeit-Approximationsalgorithmus A berechnet zur Eingabe I ∈ D in Zeit
t(|I|) eine Ausgabe σIA ∈ S(I).
Im Normalfall sind wir nur an Approximationsalgorithmen interessiert, die
eine polynomielle Laufzeit haben.
2.3
Gütegarantien
Nach obiger Definition kann ein Approximationsalgorithmus nun irgendeine
zulässige Lösung zurückgeben, unabhängig von dem Wert ihrer Zielfunktion. Natürlich möchte man aber Ausgaben zurück erhalten, die bezüglich der
Bewertungsfunktion möglichst nah an das Optimum heran kommen. Dazu betrachtet man die Qualität der Lösung des Algorithmus relativ zu der
Optimallösung und versucht eine obere Schranke für die Abweichung von
derselben zu finden.
Definition 2.3 Sei Π ein Optimierungsproblem und A ein Approximationsalgorithmus für Π.
• Bei einer Eingabe I hat A eine absolute Güte von
κA (I) = |A(I) − OPT(I)|.
• Die absolute worst-case Güte von A ist
κwc
A (n) = max{κA (I) | I ∈ D, |I| ≤ n}
• A garantiert eine absolute Güte von κA : N → N, falls ∀n ∈ N gilt:
κwc
A (n) ≤ κA (n)
Definition 2.4 Sei Π ein Optimierungsproblem und A ein Approximationsalgorithmus für Π.
• Bei einer Eingabe I hat A eine relative Güte von
A(I) OPT(I)
,
.
ρA (I) = max
OPT(I) A(I)
• Die relative worst-case Güte von A ist
ρwc
A (n) = max{ρA (I) | I ∈ D, |I| ≤ n}
3
• A garantiert eine relative Güte von ρA : N → N, falls ∀n ∈ N gilt:
ρwc
A (n) ≤ ρA (n)
• A macht bei Eingabe I einen relativen Fehler von
|A(I) − OPT(I)| A(I)
A (I) =
=
− 1
OPT(I)
OPT(I)
Für viele Probleme ist bis heute kein Approximationsalgorithmus gefunden
worden, für den man eine Gütegarantie angeben konnte. Trotzdem gibt es
häufig Algorithmen, die für einen großen Teil der Instanzen gute Näherungslösungen liefern und nur für wenige Instanzen beliebig schlecht werden. Solche Approximationsalgorithmen, für die man keine Gütegarantien angeben
kann, nennt man Heuristiken.
Kann man eine relative Güte für einen Algorithmus garantieren, möchte
man meistens auch wissen, ob die Gütegarantie eine scharfe Schranke für
die worst-case Güte eines Algorithmus ist. Man sucht also abhängig von der
Eingabelänge n Instanzen, für die der Algorithmus sehr schlechte Ergebnisse
liefert.
Definition 2.5 Sei Π ein Optimierungsproblem und A ein Approximationsalgorithmus für Π.
• A hat eine absolute Abweichung von κ0A : N → N, falls für unendlich
viele n ∈ N gilt
κ0A (n) ≤ κwc
A (n).
Eine unendlich große Menge D0 ⊆ D heißt κ0A (n)-Zeugenmenge gegen
A, wenn ∀I ∈ D0 gilt:
κA (I) ≥ κ0A (|I|).
• A hat eine relative Abweichung von ρ0A : N → N, falls für unendlich
viele n ∈ N gilt
ρ0A (n) ≤ ρwc
A (n).
Eine unendlich große Menge D0 ⊆ D heißt ρ0A (n)-Zeugenmenge gegen
A, wenn ∀I ∈ D0 gilt:
ρA (I) ≥ ρ0A (|I|).
4
3
Das Traveling Salesman Problem
Das allgemeine Traveling Salesman Problem ist wie folgt definiert:
• D = {hKn , ci | c : E → R}
• S(hKn , ci) = {C | C = (vi1 , vi2 , . . . , vin , vi1 ) ist ein Hamiltonkreis }
P
• f (C) = c(vin , vi1 ) + n−1
j=1 c(vij , vij +1 )
• ziel = min
Dabei ist Kn ein vollständiger Graph mit n Knoten V und den Kanten E.
Wie bereits eingangs erwähnt ist dieses Problem NP-schwer und es ist bis
heute nicht bekannt, ob es überhaupt in NP liegt [12, S. 9].
Aber auch der Ansatz, als Nächstes nach Approximationsalgorithmen mit
guten absoluten oder relativen Gütegarantien zu suchen, ist bei diesem Problem leider nicht von Erfolg gekrönt, wie die folgenden beiden Sätze zeigen.
So ist man bei großen Instanzen von TSP immer noch auf Heuristiken angewiesen, die für manche Eingaben nur sehr schlechte Lösungen liefern.
Satz 3.1. Falls P 6= NP gilt, gibt es keinen polynomiellen Approximationsalgorithmus mit absoluter Gütegarantie für das allgemeine TSP.
Beweis mit Gap Amplification. Annahme: Es existiert ein polynomieller Approximationsalgorithmus A, der für das TSP eine absolute Güte von k garantiert.
Wir wollen zeigen, dass unter dieser Annahme bereits ein exakter Polynomialzeitalgorithmus für TSP existiert. Dies wäre ein Widerspruch zu der
Annahme, dass P 6= NP.
Sei I = hKn , ci eine beliebige Instanz des Problems und l die kleinste Differenz zwischen dem Wert der optimalen Lösung und dem Wert einer anderen
nicht optimalen Lösung.
Nun bilden wir aus I eine neue Instanz I 0 = hKn , c0 i, mit der Gewichtsfunktion c0 = (k + 1)c.
Jede zulässige Lösung zu I entspricht nun einer zulässigen Lösung zu I 0 und
umgekehrt. Nur die Werte der Lösungen sind in I 0 (k + 1) mal größer. Damit
ist auch der Abstand zwischen der Optimallösung und einer anderen Lösung
in I 0 (k+1)l, also insbesondere echt größer als k. Damit muss der Algorithmus
A auf I 0 angewendet eine optimale Lösung OPT liefern, da sonst die absolute
5
Gütegarantie verletzt würde. Nun kann man aber auch eine optimale Lösung
für I angeben, nämlich die, die OPT entspricht.
Damit kann man aber nun mit Hilfe von A in Polynomialzeit eine optimale
Lösung für jede Instanz des TSP angeben. Dies ist ein Widerspruch zu der
Voraussetzung, dass P 6= NP.
Satz 3.2. Falls P 6= NP, gibt es keinen polynomiellen Approximationsalgorithmus mit konstanter relativer Güte r für das allgemeine TSP.
Für den Beweis siehe [12, S.53 f.].
4
Das metrische Traveling Salesman Problem
Da wir nun gesehen haben, dass man für das allgemeine TSP, falls P 6=
NP, keine Approximationsalgorithmen mit konstanten Gütegarantien finden
kann, liegt es nah, ein vermutlich leichter zu lösendes Teilproblem zu betrachten.
Bis jetzt wurden an die Gewichtsfunktion keinerlei Bedingungen gestellt.
Wenn man an die Anschauung des Problems denkt, bietet es sich an, die
Gewichte als Entfernungen zwischen den Knoten zu sehen. Dann müsste die
Gewichtsfunktion eine Metrik sein, das heißt insbesondere die Dreiecksungleichung erfüllen:
c(u, v) ≤ c(u, w) + c(w, v) ∀u, v, w ∈ V
Wegen dieser Einschränkung durch die Dreiecksungleichung wird dieses Teilproblem mit ∆TSP abgekürzt.
Des Weiteren wird in diesem Kapitel die Gewichtsfunktion auf positive, ganzzahlige Werte beschränkt (c : E → N), da es sonst zu Rundungsproblemen
kommt, wenn die Gewichtsfunktion Wurzeln enthält. Dies wäre beispielsweise der Fall, wenn man als Gewicht den euklidischen Abstand zweier Knoten
betrachtet. Bis heute ist kein Polynomialzeit-Algorithmus bekannt, der für
P √
natürliche Zahlen a1 , ..., an , m entscheiden kann, ob i ai ≤ m [2, S. 207].
Wenn man dagegen eine ganzzahlige Gewichtsfunktion verwendet, kann man
zeigen, dass das allgemeine TSP in NP liegt und damit NP-vollständig ist.
4.1
Einfüge-Heuristiken
Mit den Einfüge-Heuristiken wird eine Klasse von sehr intuitiven Algorithmen für ∆TSP vorgestellt. Die Grundidee basiert darauf, eine Anfangstour
6
Stück für Stück zu einem Hamiltonkreis zu erweitern und dabei die neuen
Knoten immer so einzufügen, dass die Tour nur minimal länger wird.
Die einzige Variable in diesem Algorithmus ist dann die Reihenfolge in der
die Knoten hinzugefügt werden. Diese Reihenfolge hat durchaus einen beträchtlichen Einfluss auf die Gütegarantien, die man geben kann. So existieren Einfügereihenfolgen und zugehörige Zeugenmengen, die zeigen, dass die
Einfüge-Heuristik eine relative Abweichung von Ω(log n/ log log n) hat [8].
Es gibt jedoch auch deutlich bessere Einfügereihenfolgen. So wird in dieser
Seminararbeit die Variante betrachtet, bei der jeweils der Knoten hinzugefügt wird, der den geringsten Abstand zu einem Knoten des Kreises hat. Der
Algorithmus heißt NearestInsertion und garantiert eine relative Güte
von 2.
Algorithmus NearestInsertion
1. Beginne mit dem Kreis C1 , der nur aus einem beliebigen Knoten besteht.
2. Füge den nächstliegenden Knoten zu C1 hinzu. Dies ergibt C2 .
3. for j := 3 to n do
(a) Wähle einen Knoten vj ∈
/ Cj−1 , der den geringsten Abstand zu
einem Knoten aus Cj−1 hat.
(b) Wähle eine Kante (u, w) aus Cj−1 , so dass c(u, vj ) + c(vj , w) −
c(u, w) minimal ist.
(c) Füge den Knoten vj zwischen u und w in Cj−1 ein. Dies ergibt
Cj .
4. done
Satz 4.1. Der Algorithmus NearestInsertion garantiert eine relative Güte von 2 bei einer Laufzeit von O(n2 )
Beweis. Für den Beweis wird der Algorithmus von Prim, der einen minimalen Spannbaum in einem Graphen berechnet, benutzt. Der Spannbaum wird
hierbei inkrementell erstellt, indem zu einem Teilbaum immer die leichteste
Kante hinzufügt wird, die den Teilbaum mit einem neuen Knoten verbindet.
Auch dieser Algorithmus startet mit einem beliebigen Knoten.2 Auffällig ist,
dass die Reihenfolge, in der die Knoten hinzugefügt werden, bei gleichem
Startknoten in beiden Algorithmen genau gleich ist. Sei nun vj der Knoten,
2
Für den genauen Algorithmus siehe auch [11]
7
der in Schritt j von beiden Algorithmen hinzugefügt wird. Mit cost(vj ) bezeichnet man die Strecke, um die sich der Kreis durch das Hinzufügen von vj
verlängert. Sei weiterhin (k, vj ) die Kante, die in diesem Schritt zum Baum
hinzugefügt wird (siehe Abbildung 1).
Es soll nun gezeigt werden, dass gilt: cost(vj ) ≤ 2c(k, vj ).
Seien u und w die beiden Knoten, zwischen denen vj in den Kreis Cj−1
eingefügt wird und sei weiterhin l ein Nachbar von k in Cj−1 .
Dann gilt: cost(vj ) = c(u, vj ) + c(vj , w) − c(u, w).
Weiter gilt cost(vj ) ≤ c(k, vj ) + c(vj , l) − c(k, l), da sonst vj zwischen k
und l hätte eingefügt werden müssen. Mit der Dreiecksungleichung gilt auch
c(vj , l) − c(k, l) ≤ c(k, vj ) und damit c(k, vj ) + c(vj , l) − c(k, l) ≤ 2c(k, vj ).
Insgesamt haben wir damit gezeigt, dass cost(vj ) ≤ 2c(k, vj ).
Da dies nun für jeden der n Schritte gilt, folgt weiter mit T dem minimalen
Spannbaum: c(Cn ) ≤ 2c(T ).
Außerdem gilt für einen Hamiltonkreis Copt minimalen Gewichts c(T ) <
c(Copt ), da man durch Weglassen einer Kante aus Copt einen Spannbaum
erhält.
Damit gilt insgesamt c(Cn ) < 2c(Copt ).
Abbildung 1: Skizze zum Beweis von Satz 4.1
4.2
Der Algorithmus von Christofides
Bereits 1976 stellte Nicos Christofides einen weiteren Approximationsalgorithmus für ∆TSP vor, der eine Güte von 1,5 besitzt [4]. Bis heute ist es
nicht gelungen, einen polynomiellen Approximationsalgorithmus zu finden,
der eine bessere Güte garantiert.
Die Idee des Algorithmus basiert darauf, zuerst einen minimalen Spannbaum
zu berechnen. Dies geht mit Prim’s Algorithmus [11] und Fibonacci-Heaps
8
in O(|E| + |V | · log |V |) [6, S. 505ff]. Aus diesem minimalen Spannbaum wird
dann mit Hilfe von leichtesten Matchings zuerst ein Eulerkreis und daraus
dann ein Hamiltonkreis konstruiert.
Ein Matching M zu einem Graph G ist ein Teilgraph in dem jeder Knotengrad höchstens 1 ist. Hat jeder Knoten genau Grad 1 so nennt man das
Matching perfekt.
Ein Kreis, der jede Kante des zugehörigen Graphen genau einmal passiert,
nennt sich Eulerkreis. Ein solcher Eulerkreis existiert genau dann, wenn G
zusammenhängend ist und jeder Knoten in G geraden Grad hat3 .
Nun können wir den Algorithmus von Christofides wie in [12] definieren:
Algorithmus CH
1. Berechne einen minimalen Spannbaum TCH von I = hKn , ci.
2. Bilde die Menge S der Knoten, die in TCH einen ungeraden Grad haben.
3. Finde auf dem durch S induzierten Teilgraphen ein perfektes Matching
minimalen Gewichts MCH .
4. Berechne einen Eulerkreis ECH auf TCH ∪· MCH .
5. Entferne in ECH Wiederholungen von Knoten, so dass man einen Hamiltonkreis C erhält und gib C aus.
Abbildung 2: Der Algoritmus von Christofides an einem Beispiel: (1) Der
minimale Spannbaum TCH , (2) das Matching MCH , (3) der Eulerkreis ECH ,
(4) der Hamiltonkreis C
Bezeichne G den gewichteten Graphen hKn , ci. Ein perfektes Matching kann
auf dem durch S induzierten Teilgraphen G0 von G nur deshalb gefunden
3
Dies zeigte Euler bereits 1736 am Beispiel des Königsberger Brückenproblems
9
werden, da |S| gerade und G0 ein vollständiger Graph ist. |S| ist immer
gerade, da die Summe aller Knotengrade eines Graphen 2|E| ist und damit
auch gerade sein muss. Dann kann die Anzahl der Knoten mit ungeradem
Grad nur gerade sein, da sonst auch die Summe aller Knotengrade ungerade
würde.
Auf dem Graphen TCH ∪· MCH lässt sich immer ein Eulerkreis berechnen, da
alle Knoten geraden Grad haben, was durch die disjunkte Vereinigung sicher
gestellt wird.
Nun soll noch die Gütegarantie 3/2 bewiesen werden.
Satz 4.2. Der Algorithmus von Christofides garantiert eine relative Güte
von 3/2.
Beweis. Da wir aus dem Eulerkreis nur noch Kanten löschen, genügt es zu
zeigen, dass c(ECH ) = c(TCH ) + c(MCH ) ≤ 32 c(Copt ).
Sei Copt ein minimaler Hamiltonkreis in G. Entfernt man eine Kante aus Copt
erhält man einen Spannbaum. Daher gilt c(TCH ) ≤ c(Copt ).
Jetzt bleibt noch zu zeigen, dass c(MCH ) ≤ 21 c(Copt ).
Dafür betrachten wir einen neuen Kreis H, der entsteht, wenn die Knoten
aus S in der Reihenfolge, in der sie in Copt vorkommen abgelaufen werden
(siehe Abbildung 3). H kann in zwei perfekte Matchings M1 und M2 zerlegt
Abbildung 3: Der Kreis H mit dem Matching M1 und gestrichelt die zusätzlichen Kanten aus Copt
werden. Ohne Einschränkung der Allgemeinheit sei jetzt c(M1 ) ≤ c(M2 ).
Dann gilt:
1
1
c(MCH ) ≤ c(M1 ) ≤ (c(M1 ) + c(M2 )) = c(H)
2
2
10
Mit der Dreiecksungleichung folgt weiterhin:
1
1
c(H) ≤ c(Copt )
2
2
Damit ist insgesamt die Gütegarantie von 3/2 gezeigt.
Die Laufzeit des Algorithmus wird von der Bestimmung eines perfekten Matchings minimalen Gewichts dominiert. Dieses Problem kann mit dem von
Edmonds beschriebenen Blossom Algorithm [7] leicht in O(n2 m) gelöst werden. Durch Lawler wurde die Laufzeit weiter auf O(n3 ) gesenkt [10] und
mittlerweile noch weiter verbessert [5].
Damit garantiert der Algorithmus von Christofides eine Güte von 3/2 bei
einer Laufzeit, die in O(n3 ) liegt.
Des Weiteren kann durch die Angabe einer Zeugenmenge gezeigt werden,
dass die bewiesene obere Schranke von 3/2 für die Güte des Algorithmus
von Christofides scharf ist [12, S. 45].
5
Das geometrische Traveling Salesman Problem
Besonders interessant ist auch das geometrische TSP. Dabei werden die Knoten mit Punkten im d-dimensionalen Raum identifiziert. Die Gewichtsfunktion c wird dann durch den Abstand zweier Punkte bezüglich einer p-Norm
ersetzt. Der Abstand muss in diesem Fall natürlich nicht ganzzahlig sein. Die
p-Norm ist wie folgt definiert:
kx, ykp =
n
X
!1/p
p
|xi − yi |
für x = (x1 , . . . , xn ) und y = (y1 , . . . , yn )
i=1
Für p = 2 entspricht dies genau der euklidischen Norm.
Für das geometrische TSP hat Arora 1996 ein so genanntes polynomielles
Approximationsschema vorgestellt [1], mit dem man das Problem mit einer
beliebigen konstanten relativen Güte größer 1 polynomiell approximieren
kann. Natürlich kann eine größere Genauigkeit nur auf Kosten der Laufzeit
erreicht werden. Trotzdem war dies ein großer Erfolg, da Arora selbst bereits
für ∆TSP gezeigt hatte, dass kein polynomielles Approximationsschema existiert, falls P 6= NP [3].
Definition 5.1 Sei Π ein Optimierungsproblem und A ein Approximati11
onsalgorithmus mit den Eingaben (0 < < 1) und der Probleminstanz I.
Dann ist A ein polynomielles Approximationsschema (PAS) für Π, wenn A in
polynomieller Zeit (in der Länge der Eingabeinstanz) eine zulässige Lösung
mit einem relativem Fehler, der kleiner als ist berechnet.
In diesem Fall approximiert der Algorithmus von Arora das geometrische
TSP mit Faktor 1 + in einer Zeit von nO(1/) .
5.1
Idee des Algorithmus
Hier wird der Algorithmus nur für den 2-dimensionalen Fall mit der euklidischen Norm gezeigt. Diesen Spezialfall nennt man euklidisches TSP. Die
Erweiterung auf alle p-Normen und den d-dimensionalen Fall ist mit kleineren Anpassungen am Algorithmus auch möglich.
Die Idee des Algorithmus beruht auf dem Divide-and-Conquer-Verfahren, bei
dem eine Probleminstanz rekursiv in Teilprobleme aufgeteilt wird, die dann
einzeln gelöst und zu einer Gesamtlösung zusammen gesetzt werden. In diesem Algorithmus wird ein Hüllquadrat rekursiv in Teilquadrate aufgeteilt
und es wird festgelegt, dass ein Hamiltonkreis eine so entstandene Grenzlinie zwischen den Quadraten nur O(1/) mal überschreiten darf. Dann wird
mittels dynamischer Programmierung ein solcher Hamiltonkreis gefunden.
5.2
Rundung
Sei I = hGi eine Probleminstanz des euklidischen TSP, wobei G ein vollständiger Graph mit Knoten v ∈ R2 ist. Sei OPT die Länge eines minimalen
Hamiltonkreises Copt in G. Zuerst wird durch eine leichte Verschiebung der
Knoten sichergestellt, dass sie alle auf einem Einheitsgitter liegen und damit
ganzzahlige Koordinaten haben. Des Weiteren sollen danach alle Knotendistanzen, die nicht 0 sind, mindestens 2 sein und die maximale Distanz
zwischen zwei Knoten soll höchstens n2 /2 sein.
Dafür wird das kleinste achsenparallele Quadrat gefunden, das alle Knoten
einschließt. Dieses Quadrat wird Hüllquadrat genannt und hat eine Seitenlänge l. Sei d die größte Entfernung zwischen zwei Knoten in G. Mit einem
3
Gitter bei dem die Gitterlinien einen Abstand von d/n 2 von einander haben
1
und der Annahme, dass > 1/n 3 gilt, lassen sich alle obigen Bedingungen
erfüllen [2, S. 210]. Dafür werden alle Knoten auf den nächstgelegenen Gitterpunkt verschoben und die Distanzen so skaliert, dass zwei Gitterpunkte
den Abstand 2 haben. In dem Fall, dass zwei Knoten auf den selben Gitterpunkt fallen, werden diese erst einmal wie ein einziger Knoten behandelt
12
und dann vor der Ausgabe wieder aufgesplittet.
Abbildung 4: Verschieben der Knoten auf Gitterpunkte
Durch diese Verschiebung der Knoten wird die Länge der optimalen Tour
1
um höchstens d/n 2 verändert, was im Verhältnis zu der vorgeschriebenen
höchsten Abweichung von ·OPT für große n vernachlässigbar ist.
5.3
Partitionierung
Die Partitionierung erfolgt randomisiert. Dafür betrachtet man ein weiteres
achsenparalleles Quadrat Q, dessen Seitenlänge 2l ist und das mit dem linken
unteren Eckpunkt auf dem linken unteren Eckpunkt des Hüllquadrats liegt.
Seien nun a und b zufällig gewählte ganze Zahlen im Bereich von 0 bis l. Nun
wird Q um a Einheiten nach links und b Einheiten nach unten verschoben,
das entstehende Quadrat wird Q0 genannt. Da Q0 das Hüllquadrat unabhängig von a und b vollständig überdeckt, beinhaltet eine Partitionierung von
Q0 automatisch eine Partitionierung des Hüllquadrats und damit des ganzen
Graphen G.
Die Partitionierung von Q0 wird mittels Quadtrees realisiert. Dabei wird das
Wurzelquadrat rekursiv so lange in vier gleich große Kindquadrate zerlegt bis
jedes Blattquadrat höchstens einen Knoten enthält (siehe auch Abbildung
5). Ohne Beschränkung der Allgemeinheit wird hierbei angenommen, dass
die Seitenlänge 2l von Q0 eine Zweierpotenz ist.
Genauso wie den Teilquadraten im Quadtree eine Tiefe zugeordnet ist, kann
man nun auch den beiden Linien, die ein Quadrat zerteilen, dessen Tiefe
zuordnen. Damit so auch alle Gitterlinien eine Tiefe zugeordnet bekommen,
weist man ihnen die Tiefe zu, die sie hätten, wenn die Partitionierung fortgesetzt würde bis alle Blattquadrate Seitenlänge 1 hätten.
Wichtig für den Algorithmus ist, dass alle Gitterlinien in dem Hüllquadrat
mit gleicher Wahrscheinlichkeit in der Partitionierung eine Linie der Tiefe
13
Abbildung 5: Beipiel einer randomisierten Partitionierung
i sind. Dies ist durch die Partition und zufällige Verschiebung des größeren
Quadrats gegeben.
Die Wahrscheinlichkeit ergibt sich dadurch, dass es 2i äquidistante Linien
der Tiefe i gibt, wie folgt:
Proba (die Gitterlinie hat Tiefe i) =
5.4
2i
2l
Portale
Die möglichen Touren sollen jetzt so beschränkt werden, dass sie nur noch
über bestimmte Punkte auf den Linien, Portale genannt, zwischen Quadraten
wechseln können. Auf einer Linie mit Tiefe i gibt es 2i+1 m äquidistante
Portale. Die Konstante m heißt der Portalparameter und wird in unserem
Fall auf O(log(n)/) festgelegt. Außerdem ist jede Ecke eines Quadrates ein
Portal. Da eine Linie der Tiefe i auf jeder Seite zu 2i+1 Quadraten der Tiefe
i + 1 benachbart ist, hat jedes Quadrat höchstens 4m + 4 Portale.
Als Nächstes wird mittels dynamischer Programmierung eine möglichst kurze Tour gefunden, die alle Knoten besucht und die Grenze zwischen zwei
Quadraten nur durch Portale überschreitet. Dies ist in einer Zeit von nO(1/)
möglich.
Als letztes bleibt dann noch zu zeigen, dass die optimale portalrespektierende Tour mit einer Wahrscheinlichkeit von mindestens 1/2 eine (1 + )Approximation für OPT ist.
14
5.5
Der Algorithmus
Eine erste Einsicht ist, dass eine optimale portalrespektierende Tour jedes
Portal höchstens zweimal benutzt. Andernfalls kann mit Verwendung der
Dreiecksungleichung leicht eine kürzere Tour gefunden werden.
Damit wird die Grenze zu jedem Quadrat höchstens 8m + 8 mal überschritten.
Der Algorithmus berechnet jetzt zuerst wie oben beschrieben eine Partitionierung. Dies kann effizient durch die Sortierung der Knoten nach ihren
Koordinaten geschehen. Von unten nach oben im Quadtree wird für jedes
Quadrat und alle Möglichkeiten Portale auszuwählen und zu kombinieren
eine optimale Teiltour innerhalb dieses Quadrats berechnet und in einer Tabelle gespeichert. Es gibt natürlich für jedes Quadrat viele Möglichkeiten,
Portale auszuwählen und durch Wege zu verbinden. Wie viele das sind wird
jetzt noch abgeschätzt.
Einerseits darf jedes Portal höchstens zweimal benutzt werden. Dies entspricht bei 4m + 4 Portalen 34m+4 Möglichkeiten die Portale auszuwählen.
Es gilt 34m+4 = 2(4m+4) log 3 = 2O(log n/) = nO(1/)
Andererseits kann eine optimale Tour wegen der Dreiecksungleichung keine
Kreuzungen enthalten und damit können die Pfade zwischen den ausgewählten Portalen nur so gezogen werden, dass die so entstehenden Paare von
Portalen einem gültigen Klammerausdruck entsprechen (siehe auch Abbildung 6). Die Anzahl der gültigen Klammerausdrücke für 2s Klammern ist
1 2s
2s
die Catalanzahl Cs = s+1
s . Diese ist kleiner als 2 , da dies der Anzahl
aller möglichen (nicht unbedingt gültigen) Klammerausdrücken entspricht.
Da jedes Quadrat höchstens 8m+8 mal betreten bzw. verlassen werden kann
ist die Anzahl der zu betrachtenden Paarungen für die ausgewählten Portale
kleiner als 28m+8 = 2O(log n/) = nO(1/) .
Damit ist die Anzahl der gültigen Auswahlen und Kombinationen von Portalen für ein Quadrat insgesamt auch (nO(1/) )2 = nO(1/) .
Um die optimalen Touren zu berechnen, wird für die Blattquadrate im
Quadtree, die alle nur höchstens einen Knoten enthalten, in O(m) Zeit ausprobiert, in welchen Pfad von einem Portal zum anderen man diesen Knoten
einfügen muss (siehe Abbildung 6).
Für innere Knoten des Quadtrees betrachtet der Algorithmus alle Möglichkeiten, wie eine portalrespektierende Tour die Grenzen zwischen seinen vier
Kindern überschreiten kann. Für jede dieser Möglichkeiten berechnet der
Algorithmus die Kosten einer solchen Tour indem er die Summe der Kosten
der optimalen Touren für die Kinder bildet. Zwischen diesen Kindern gibt
15
Abbildung 6: Beispiel für eine portalrespektierenden Tour innerhalb eines
Blattquadrats
es 4m + 1 Portale. Für die Anzahl an zulässigen Möglichkeiten kann man
ähnlich wie eben zeigen, dass diese in nO(1/) liegt.
Der Quadtree hat höchstens 2n Blätter, da von je vier benachbarten Blättern
höchstens zwei keinen Knoten enthalten können, sonst wäre die Partitionierung schon einen Schritt vorher abgebrochen worden. Damit liegt die Anzahl
der Quadrate insgesamt in O(n log n).
Insgesamt hat der Algorithmus nun eine Laufzeit von nO(1/) , da alle anderen
linearen oder logarithmischen Faktoren von diesem Faktor dominiert werden.
Da der Algorithmus am Ende auch eine optimale portalrespektierende Tour
für das Wurzelquadrat berechnet, das den gesamten Graphen enthält, findet
er auch die optimale portalrespektierende Tour in dem Graphen G.
5.6
Analyse der Gütegarantie
Zu zeigen bleibt noch, dass die Länge der optimalen portalrespektierenden
Tour OPTm,a,b ) mit einer Wahrscheinlichkeit von mindestens 1/2 eine (1+)Approximation für OPT ist.
Sei d(u, v) die euklidische Distanz von u und v und da,b (u, v) die portalrespektierende Distanz von u und v, das heißt die Länge des kürzesten portalrespektierenden Wegs zwischen u und v.
Satz 5.1. Der Erwartungswert von da,b (u, v) − d(u, v) ist höchstens
log(2l)
d(u, v).
m
Beweis. Die Strecke (u, v) kreuzt höchstens 2d(u, v) Gitterlinien. Die por16
Abbildung 7: Skizze des portalrespektierenden Weges aus dem Beweis von
Satz 5.1
talrespektierende Distanz kann dadurch nach oben abgeschätzt werden, dass
man die Länge des portalrespektierenden Wegs verwendet, der an jeder Gitterlinie von dem optimalen Weg aus einen Umweg zu dem nächsten Portal
und wieder zurück macht (siehe Abbildung 7). Ein solcher Umweg ist für eine
Gitterlinie der Tiefe i höchstens 2l/m2i+1 lang, was dem Abstand zwischen
zwei Portalen auf dieser Linie entspricht. Die Wahrscheinlichkeit dafür, dass
eine Gitterlinie die Tiefe i hat ist wie bereits gezeigt 2i /2l. Damit ist der
Erwartungswert für die Länge des Weges
2d(u, v)
X 2i
i
X 1
2l
log(2l)
=
d(u,
v)
=
d(u, v).
i+1
2l m2
m
m
·
i
Wenn man nun OPTm,a,b nach oben durch die Länge der Tour abschätzt,
die entsteht, wenn man die optimale Tour Copt portalrespektierend macht,
dann ist der Erwartungswert von OPTm,a,b − OPT höchstens log(2l)
· OPT.
m
Mit einer Wahrscheinlichkeit von mindestens 1/2 ist OPTm,a,b − OPT dann
kleiner als der doppelte Erwartungswert 2 log(2l)
· OPT.
m
Es gilt l ≤ n2 /2 und wenn man jetzt noch m ≥ 4 log n/ wählt, gilt insgesamt
2 log(2l)
2 log(n2 )
4 log n
· OPT ≤
· OPT ≤
· OPT ≤ · OPT.
m
4 log n
4 log n
Damit ist OPTm,a,b ≤ (1 + )OPT mit einer Wahrscheinlichkeit von mindestens 1/2.
Insgesamt ist nun die Korrektheit und die Abhängigkeit der Laufzeit von der
gewünschten Güte bewiesen und damit der Algorithmus von Arora ein PAS
für geometrisches TSP.
17
Literaturverzeichnis
[1] Sanjeev Arora. Polynomial time approximation schemes for Euclidean TSP and other geometric problems. In Foundations of Computer
Science. Proceedings., 37th Annual Symposium, 1996.
[2] Sanjeev Arora. Approximation algorithms for geometric TSP. In Gregory Gutin, editor, The traveling salesman problem and its variations.
Springer, 2007.
[3] Sanjeev Arora, Carsten Lund, Rajeev Motwani, Madhu Sudan, and Mario Szegedy. Proof verification and the hardness of approximation problems. Journal of the ACM, 45, 1998.
[4] Nicos Christofides. Worst-case analysis of a new heuristic for the travelling salesman problem. Technical Report 388, Graduate School of
Industrial Administration, Carnegie Mellon University, 1976.
[5] William Cook and Andre Rohe. Computing minimum-weight perfect
matchings. INFORMS Journal on Computing, 11, 1999.
[6] Thomas H. Cormen, Clifford Stein, Ronald L. Rivest, and Charles E.
Leiserson. Introduction to Algorithms. McGraw-Hill Higher Education,
2001.
[7] Jack Edmonds. Paths, trees, and flowers. Canadian Journal of Mathematics, 17, 1965.
[8] Dorit S. Hochbaum, editor. Approximation algorithms for NP-hard problems. PWS Publishing Co., 1997.
[9] Richard M. Karp. Reducibility among combinatorial problems. In Complexity of Computer Computations. Plenum Press, 1972.
[10] Eugene L. Lawler. Combinatorial optimization: networks and matroids.
Holt, Rinehart and Winston, 1976.
[11] Robert C. Prim. Shortest connection networks and some generalizations.
Bell System Technology Journal, 36, 1957.
[12] Rolf Wanka. Approximationsalgorithmen : Eine Einführung. B.G. Teubner Verlag, 2006.
18