Übungsblatt 5 (22.06.2012) - Lehrstuhl für Optik, Uni Erlangen

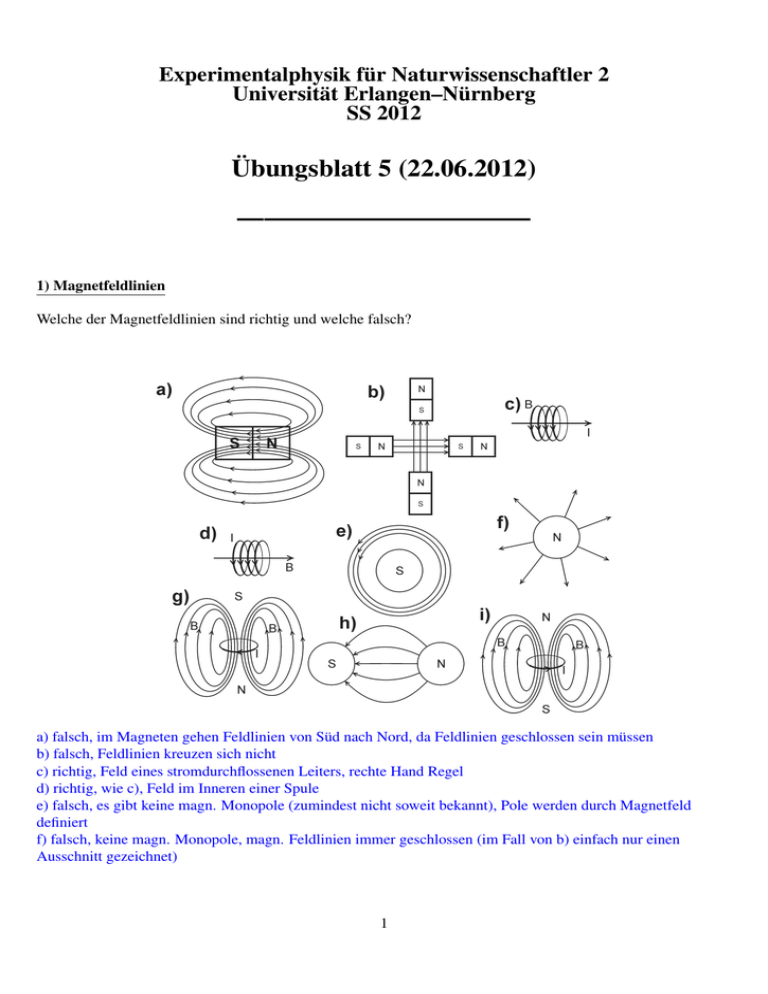
Experimentalphysik für Naturwissenschaftler 2
Universität Erlangen–Nürnberg
SS 2012
Übungsblatt 5 (22.06.2012)
———————————
1) Magnetfeldlinien
Welche der Magnetfeldlinien sind richtig und welche falsch?
a) falsch, im Magneten gehen Feldlinien von Süd nach Nord, da Feldlinien geschlossen sein müssen
b) falsch, Feldlinien kreuzen sich nicht
c) richtig, Feld eines stromdurchflossenen Leiters, rechte Hand Regel
d) richtig, wie c), Feld im Inneren einer Spule
e) falsch, es gibt keine magn. Monopole (zumindest nicht soweit bekannt), Pole werden durch Magnetfeld
definiert
f) falsch, keine magn. Monopole, magn. Feldlinien immer geschlossen (im Fall von b) einfach nur einen
Ausschnitt gezeichnet)
1
g) richtig, Feld einer Leiterschleife, bzw. Spule
h) falsch, keine magn. Monopole, Feldlinien wie E-Feldlinien senkrecht auf Oberfläche wäre für Ladung richtig
i) falsch) Strom bzw. Magnetfeld zeigt in falsche Richtung, Norden und Süden vertauscht
2) Induktion
Eine Kupferschleife r = 20 cm (siehe Skizze) rotiert in einem Magnetfeld von B0 = 0, 20 T mit einer Frequenz
von f = 50 Hz.
a) Berechnen Sie die Induktionsspannung U (t)
Das Magnetfeld ist stationär und homogen, auch die von der Leiterschleife umschlossene Fläche
∫ ist konstant,
⃗ A.
⃗
jedoch ändert sich der Anteil des durch die Fläche tretenden Feldes, also der magn. Fluss Φ = Bd
∫
∫
∂
∂
⃗
⃗
U (t) = −Φ̇ = −
BdA = −
B0 cos (ωt) dA
∂t A
∂t A
∫
∫
=
B0 ω sin (ωt) dA = B0 ω sin (ωt) dA = B0 ω sin(ωt) · r2 π = U0 sin(ωt)
A
A
U0 = B0 2πf · r2 π = 7, 9 V
Das Vorzeichen hängt von der Richtung des Magnetfeldes, der Wahl der Flächennormalen oder des
Zeitnullpunktes/Startwinkels, sprich den Anfangsbedingungen, ab.
b) Wie schnell muss die Schleife rotieren, um eine Spitzenspannung von U0 = 100 V zu generieren?
Gesucht ist die Amplitude U0 , da sin(ωt) maximal 1 werden kann.
U0 = B0 ωr2 π = 100 V
U0
ω
=
= 633 Hz
2π
B0 2r2 π 2
c) Welche weiteren Möglichkeiten der Spannungsregelung gibt es?
Zum einen könnte das Magnetfeld reguliert werden, zum anderen könnte der Fluss geändert werden, indem man
den Winkel der Rotationsachse der Leiterschleife, welche in der Skizze senkrecht zum Magnetfeld steht,
verkleinert. Allerding bietet die zweite Möglichkeit nur eine Abschwächung der Amplitude, während die erste
auch eine Verstärkung der Spitzenspannung zulässt.
f=
2
Durch eine Änderung der Fläche ließe sich die Spannung ebenfalls verändern, jedoch auch hier nur zu
niedrigeren Spannungen hin, da der Kreis bereits die größtmögliche Fäche hat, die man mit dem Draht
einschließen kann.
3) Wasser-Kondensator
Ein Kondensator mit den quadratischen Flächen der Kantenlänge a = 10 cm2 und Abstand d = 1 cm kann mit
Wasser (ϵr = 80, 1) befüllt werden.
a) Wie groß ist die Kapazität des Kondensators vor dem Befüllen?
C0 = ϵ0
A
a2
= ϵ0 = 8, 85 · 10−12 F = 8, 85 pF
d
d
b) Bei welchem Füllstand h erhält man die 30-fache Kapazität des leeren Kondensators?
Wasserkondensator und Luftkondensator parallel geschaltet
C(h) = C0 (h) + CW (h) = ϵ0
a(a − h)
ah
ϵ0 a
A
+ ϵ0 ϵr
=
(a + h(ϵr − 1)) = 30C0 = 30ϵ0
d
d
d
d
⇔ a + h(ϵr − 1) = 30a
29a
⇔h=
= 3, 67 cm
ϵr − 1
c) Wie ändert sich die Kapazität, wenn man nun den Kondensator um 90◦ dreht, so dass das Wasser eine der
Platten komplett bedeckt?
Reihenschaltung zweier Kondensatoren, einmal mit Wasser der Dicke dW und einmal mit Luft der Dicke
d − dW , die Pattenfläche ist bei beiden a2
VW asser = adh
⇒ dW =
dh
VW asser
=
2
a
a
1
1
d − dW
dW
dϵr + dW (1 − ϵr )
1
=
+
=
+ 2
=
2
C90
CL CW
a ϵ0
a ϵ0 ϵr
a2 ϵ0 ϵr
a3 ϵ0 ϵr
⇔ C90 =
= 13, 9 pF
dϵr a + dh(1 − ϵr )
3