TU München, Fakultät für Informatik Lehrstuhl III: Datenbanksysteme

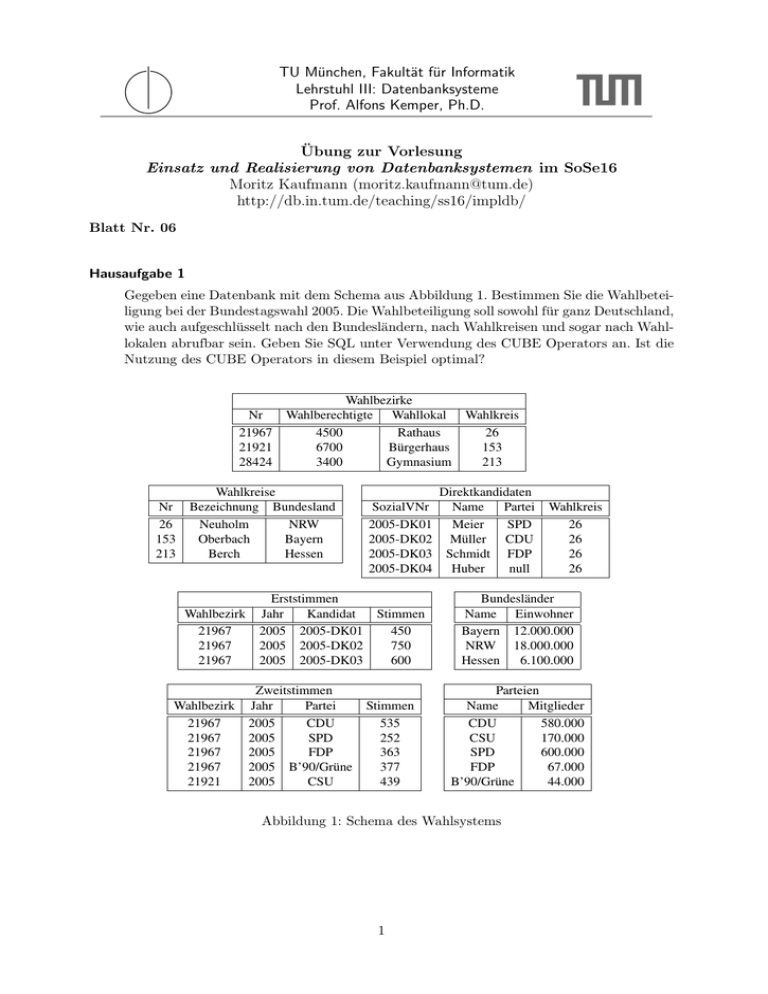
TU München, Fakultät für Informatik
Lehrstuhl III: Datenbanksysteme
Prof. Alfons Kemper, Ph.D.
Übung zur Vorlesung
Einsatz und Realisierung von Datenbanksystemen im SoSe16
Moritz Kaufmann ([email protected])
http://db.in.tum.de/teaching/ss16/impldb/
Blatt Nr. 06
Hausaufgabe 1
Gegeben eine Datenbank mit dem Schema aus Abbildung 1. Bestimmen Sie die Wahlbeteiligung bei der Bundestagswahl 2005. Die Wahlbeteiligung soll sowohl für ganz Deutschland,
wie auch aufgeschlüsselt nach den Bundesländern, nach Wahlkreisen und sogar nach Wahllokalen abrufbar sein. Geben Sie SQL unter Verwendung des CUBE Operators an. Ist die
Nutzung
!!" des CUBE Operators in diesem Beispiel optimal?
#$ %&'()*)'(+,*'-'
+)
12345
12312
1>616
+)
14
27=
12=
!"#$%&'()*&
!"#$%&)&,#-(.-& !"#$$/*"$
6788
9"-#":0
4588
;<).&)#":0
=688
?@AB"0(:A
!"#$*)&(0&
;&'&(,#B:B. ;:BC&0$"BC
+&:#/$A
+9!
D%&)%",#
;"@&)B
;&),#
E&00&B
!"#$%&'()*
12345
12345
12345
!"#$%&'()*
12345
12345
12345
12345
12312
G/'("$H+)
1887JFK82
1887JFK81
1887JFK8=
1887JFK86
P)0-0-(AA&B
Q"#)
K"BC(C"1887 1887JFK82
1887 1887JFK81
1887 1887JFK8=
US&(-0-(AA&B
Q"#)
I")-&(
1887
MFN
1887
GIF
1887
OFI
1887 ;V38W?)<B&
1887
MGN
G-(AA&B
678
578
488
G-(AA&B
7=7
171
=4=
=55
6=3
!"#$*)&(0
14
27=
12=
F()&*-*"BC(C"-&B
+"A&
I")-&(
L&(&)
GIF
L<$$&) MFN
G,#A(C- OFI
E:%&)
B:$$
!"#$*)&(0
14
14
14
14
;:BC&0$RBC&)
+"A& P(BS/#B&)
;"@&)B 21T888T888
+9! 2>T888T888
E&00&B
4T288T888
I")-&(&B
+"A&
L(-.$(&C&)
MFN
7>8T888
MGN
258T888
GIF
488T888
OFI
45T888
;V38W?)<B&
66T888
X%%($C:B. 7T1Y O(*-(Z& X:0[)R.:B. C&) ;:BC&0-".0S"#$&).&%B(00& 1887
Abbildung 1: Schema des Wahlsystems
.*)/(*0
D%(.&0 )&$"-(/B"$&0 G,#&A" &B-#R$- &(B&B \:B.&)(,#-&-&B] U@*$:0 *"0*"C(&)&BC&) M/B0-)"(B-J
F&^B(-(/B&B_ C&) C(& 9&$"-(/B&B !"#$#$%&&'(_ )%"'*$*+(,%,+$'(_ -+./0'1%"*' :BC -+./2
*"'%#' &(B0,#$(&`-Y
1
-+./0'1%"*'
!"#$#$%&&'(
-+./*"'%#'
Die Lösung für die Formulierung der Anfrage mithilfe des CUBE operators ist im
Lösungsbuch.
Ergänzend noch die Antwort zur Frage ob der CUBE Operator für diese Anfrage
optimal ist: Der CUBE Operator wird typischerweise mit unabhängigen Dimensionen genutzt. Der Operator berechnet dann fur alle Kombinationsmöglichkeiten der
Dimensionen für die Aggregation. Für die Aufgabe ergeben sich damit folgende Kombinationen:
{Bundesländer, Wahlkreise, Wahllokale}, {Bundesländer, Wahlkreise}, {Bundesländer, Wahllokale}, {Wahlkreise, Wahllokale}, {Bundesländer}, {Wahlkreise}, {Wahllokale}, {}
Da in diesem Beispiel die verschiedenen CUBE Dimensionen nicht unabhängig sind,
sondern hierarchisch aufgebaut sind, finden redundante Berechnungen statt. Bundesländer, Wahlkreise und Wahlkreise produzieren beide jeweils gleichgroße Ergebnismengen mit den gleichen aggregierten Werten. Bei hierarchischen Daten wie in diesem
Beispiel wäre der ROLLUP operator besser geeignet.
Hausaufgabe 2
tätschema.
Lösen sie folgende Anfrage mit SQL basierend auf dem bekannten Universi-
1. Bestimmen Sie die Durchschnittsnote für jeden Studenten.
2. Basierend auf dieser Durchschnittsnote, bestimmen Sie für alle Studenten ihren Rangplatz innerhalb ihrer Kohorte (Studenten desselben Semesters).
3. Berechnen Sie zusätzlich für jeden Studenten auch noch die ABWEICHUNG seiner
Durchschnittsnode von der Durchschnittsnote der Kohorte (also vom Durchschnitt
der Durchschnittsnote der Studenten der Kohorte) ausgegeben werden.
Lösen Sie Teilaufgaben b und c jeweils einmal mit und einmal ohne Nutzung von Windowfunktionen. Ihre Anfragen können Sie auf hyper-db.de testen. Nutzen sie folgende
erweiterte pruefen Relation:
with mehr_pruefen ( MatrNr , VorlNr , PersNr , Note ) as (
select * from pruefen
union
values (29120 ,0 ,0 ,3.0) , (29555 ,0 ,0 ,2.0) , (29555 ,0 ,0 ,1.3) , (29555 ,0 ,0 ,1.0)
)
2
Ohne Windowfunktionen:
with mehr_pruefen ( MatrNr , VorlNr , PersNr , Note ) as (
select * from pruefen
union
values (29120 ,0 ,0 ,3.0) , (29555 ,0 ,0 ,2.0) , (29555 ,0 ,0 ,1.3) , (29555 ,0 ,0 ,1.0)
),
noten ( MatrNr , Semester , Note ) as (
select s . matrnr , semester , avg ( Note )
from studenten s , mehr_pruefen p
where s . matrnr = p . matrnr
group by s . matrnr , semester
)
select * ,
( select count (*)+1 from noten x
where x . Semester = n . Semester and x . Note < n . Note ) as Rang ,
( select avg ( x . Note ) from noten x
where x . Semester = n . Semester ) as GPA ,
( select avg ( x . Note ) from noten x
where x . Semester = n . Semester ) - note as Abweichung
from noten n order by semester , rang
Mit Windowfunktionen:
with mehr_pruefen ( MatrNr , VorlNr , PersNr , Note ) as (
select * from pruefen
union
values (29120 ,0 ,0 ,3.0) , (29555 ,0 ,0 ,2.0) , (29555 ,0 ,0 ,1.3) , (29555 ,0 ,0 ,1.0)
),
noten ( MatrNr , Semester , Note ) as (
select s . matrnr , semester , avg ( Note )
from studenten s , mehr_pruefen p
where s . matrnr = p . matrnr
group by s . matrnr , semester
)
select * ,
rank () over ( partition by Semester order by Note desc ) as Rang ,
avg ( Note ) over ( partition by Semester ) as GPA ,
avg ( Note ) over ( partition by Semester ) - note as Abweichung
from noten order by semester , rang
Hausaufgabe 3
Die in Abbildung 2 dargestellten Relationen Mietspiegel und Kindergarten dienen der
Bewertung von Wohngegenden im Großraum München. Für eine junge Familie ist ausschlaggebend, wie hoch die Lebenshaltungskosten gemessen an zu zahlender Miete und zu
entrichtender Gebühr für den Kindergarten im jeweiligen Wohnort ausfallen. Illustrieren
Sie die Ausführung einer Top-1-Berechnung (zur Bestimmung des günstigsten Wohnorts)
für eine junge Familie mit zwei Kindern. Zeigen Sie die phasenweise Berechnung des Ergebnisses jeweils mit dem Threshold- und dem NRA-Algorithmus.
Siehe Lösungsbuch
3
!"#
$%& '()*+(,-+./( 012(13415(16 789:; <=)= >=*(/?4@(; <=)= A+1+15
!"#$%&"#'#(
)*$
!"#$#
+,*-."/'
011
2%3,/"/'
411
5/$#*67.*"/'
8111
9:3&.#/;<*' 8=11
>?'#/.,<%#/
8@11
+*A/B,(C
8D11
E"/C#*',*$#/
)*$
>#"$*,'
+*A/B,(C
F811
5/$#*67.*"/'
1
>?'#/.,<%#/
811
2%3,/"/'
G11
+,*-."/'
G=1
9:3&.#/;<*'
H11
I?./J,'#
)*$
+*A/B,(C
5/$#*67.*"/'
2%3,/"/'
+,*-."/'
>?'#/.,<%#/
9:3&.#/;<*'
J,'#
!A/-.#/FKAC
!A/-.#/F9?*C
!A/-.#/F9?*C
!A/-.#/F9?*C
!A/-.#/FL"$:
!A/-.#/FL"$:
M;;"(C</' 8DN@O !A/-.#/#* I?./(,'#/ P<* >#*#-./</' C#* 3?/,$("-.#/ E?%$#/ 6A* #"/#
Abbildung 2: Münchner Wohnlagen zur Berechnung der monatlichen Kosten für eine Familie.
Q,3"("#O !"#$# </C E"/C#*',*$#/
04B5=,( $%&$$
R"# "/ M;;"(C</' 8DN@ ST('N ,<-. K#"$# =HU VE#3&#* </C W"-X(#* SG114YZY C,*'#%$#((F
$#/ [#(,$"?/#/ !"#$%&"#'#( </C )"*+#,'-,$#* C"#/#/ C#* >#B#*$</' T?/ I?./'#'#/C#/
"3 +*?\*,<3 !A/-.#/N QA* #"/# ]</'# Q,3"("# "%$ ,<%%-.(,''#;#/C^ B"# .?-. C"# J#F
;#/%.,($</'%X?%$#/ '#3#%%#/ ,/ P< P,.(#/C#* !"#$# </C P< #/$*"-.$#/C#* +#;A.* 6A*
C#/ E"/C#*',*$#/ "3 ]#B#"("'#/ I?./?*$ ,<%6,((#/N 2((<%$*"#*#/ K"# C"# M<%6A.*</' #"/#*
_?&F8F>#*#-./</' SP<* >#%$"33</' C#% 'A/%$"'%$#/ I?./?*$#%Y 6A* #"/# ]</'# Q,3"("#
3"$ PB#" E"/C#*/N `#"'#/ K"# C"# &.,%#/B#"%# >#*#-./</' C#% W*'#;/"%%#% ]#B#"(% 3"$
C#3 _.*#%.?(CF </C C#3 9[MFM('?*"$.3<%N
R"# M/6*,'# (a%%$ %"-. 3"$$#(% KbJ ;#"%&"#(%B#"%# B"# 6?('$ 6?*3<("#*#/OH
!"#"$% !"#$%& !"'()%) * +,-".)(%$/0 &! 123%)4
'()* '()%35()0)6 !& 1(47)$0/$%)4 +,"(" !"#$% 8 -"#$%
)(-"( ./ 123%)4
'"%$, '0(!% 9 ()+! )1#/
`<* M<%B#*$</' C"#%#* M/6*,'# X7//#/ C#* _.*#%.?(CF </C C#* 9[MF S./ 0-*+/1 234
3#%%Y M('?*"$.3<% T#*B#/C#$ B#*C#/N >#"C# %#$P#/ ,<6 #"/#* ,<6%$#"'#/C#/ K?*$"#*</'
C#* ;#$#"("'$#/ [#(,$"?/#/ !"#$%&"#'#( </C4 )"*+#,'-,$#* ,<6N K-.*"$$B#"%# B#*C#/ ]#F
B#"(% C"# /a-.%$#/ _<&#( "/ C#/ W"/',;#*#(,$"?/#/ '#(#%#/ </C ,<%'#B#*$#$N Ia.*#/C
C#* _.*#%.?(CFM('?*"$.3<% T?*,<%%#$P$^ C,%% ,<6 /?-. ,<%%$#.#/C# W"/P#(;#B#*$</'#/
S!"#$# </C >#"$*,'Y B,.(6*#" P<'#'*"66#/ B#*C#/ X,//^ "%$ C"#% ;#"3 9[M /"-.$ 37'("-.