1.3 Elektrisches Feld, El. Feldstärke 1.3 Elektrisches Feld, El

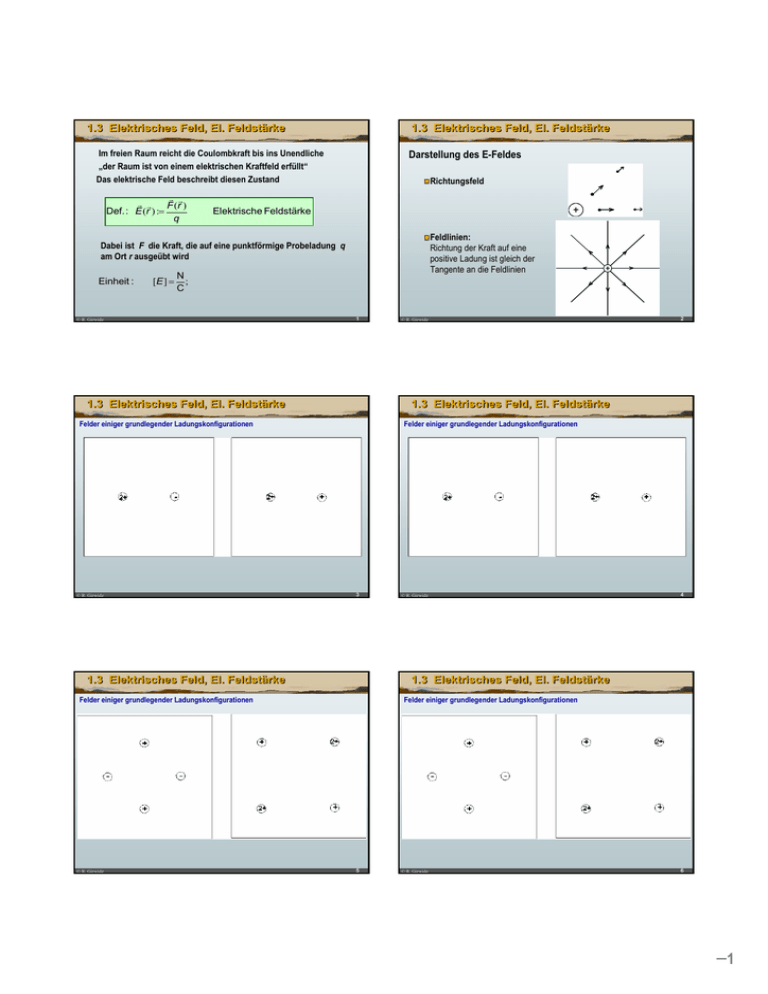
1.3 Elektrisches Feld, El. Feldstärke
1.3 Elektrisches Feld, El. Feldstärke
Im freien Raum reicht die Coulombkraft bis ins Unendliche
„der Raum ist von einem elektrischen Kraftfeld erfüllt“
Das elektrische Feld beschreibt diesen Zustand
r r
r r
F (r )
Def. : E (r ) :=
q
Darstellung des E-Feldes
Richtungsfeld
Elektrische Feldstärke
Feldlinien:
Richtung der Kraft auf eine
positive Ladung ist gleich der
Tangente an die Feldlinien
Dabei ist F die Kraft, die auf eine punktförmige Probeladung q
am Ort r ausgeübt wird
Einheit :
[E ] =
N
;
C
© R. Girwidz
1
1.3 Elektrisches Feld, El. Feldstärke
Felder einiger grundlegender Ladungskonfigurationen
3
1.3 Elektrisches Feld, El. Feldstärke
© R. Girwidz
4
1.3 Elektrisches Feld, El. Feldstärke
Felder einiger grundlegender Ladungskonfigurationen
© R. Girwidz
2
1.3 Elektrisches Feld, El. Feldstärke
Felder einiger grundlegender Ladungskonfigurationen
© R. Girwidz
© R. Girwidz
Felder einiger grundlegender Ladungskonfigurationen
5
© R. Girwidz
6
–1
1.3 Elektrisches Feld, El. Feldstärke
1.3 Elektrisches Feld, El. Feldstärke
Felder einiger grundlegender Ladungskonfigurationen
Feldlinien
7
© R. Girwidz
1.3 Elektrisches Feld, El. Feldstärke
8
© R. Girwidz
1.3 Elektrisches Feld, El. Feldstärke
Berechnung elektrischer Felder
Charakteristika des E-Feldes
Feld einer Punktladung:
"Quellen- und Senkenfeld"
Ladungen sind Quellen und Senken des E-Feldes
(Feldlinien beginnen bzw. enden in Ladungen oder Singularitäten des
Feldes)
r
r r
1 Qr
E (r ) =
4πε 0 r 3
r
1 Q
E =
4πε 0 r 2
Das (elektrostatische) E-Feld ist wirbelfrei
Es gibt keine geschlossenen Feldlinien / keine Wirbel
Feldstärke bei einer diskreten Ladungsverteilung
und Superpositionsprinzip
(siehe Aufgabe)
9
© R. Girwidz
1.3 Elektrisches Feld, El. Feldstärke
1.3 Elektrisches Feld, El. Feldstärke
Dipolfeld (Berechnungen siehe Beispielaufgaben)
– Def. Dipolvektor:
10
© R. Girwidz
Felder kontinuierlicher
Ladungsverteilungen (siehe
Aufgaben)
pe = q * a
– Feldstärke auf der Dipolachse (x-Achse)
– Feldstärke auf der Mittelsenkrechten zur Dipolachse (y-Achse)
(siehe Rechnungen)
– Allgemein:
E (r ) =
© R. Girwidz
1 3( p * r )r − (r * r )p
4πε 0
r5
11
© R. Girwidz
12
–2
1.3 Elektrisches Feld, El. Feldstärke
1.4 Gaußsches Gesetz
Rechenbeispiel: Stab mit homogener Linienladungsdichte (siehe Rechnung)
"Quellen- und Senkenfeld math. erfasst"
A) Definitionen
E
Elektrischer Fluss
Φ = ∫ ε rε 0 ⋅ E d A
A
dA
ε r = 1 im Vakuum
Elektrische Flussdichte /
dielektrische Verschiebung
D = εrε0 ⋅ E
13
© R. Girwidz
1.4 Gaußsches Gesetz
14
© R. Girwidz
1.4 Gaußsches Gesetz
B) Gesetz von Gauß
C) Anwendung bei charakteristischen Feldverteilungen
Der Gesamtfluss durch eine
beliebige geschlossene
Oberfläche ist gleich der
eingeschlossenen Gesamtladung
ΦGes = ∫ ε 0 ⋅ E d A = Qinnen
Der Flächenvektor steht senkrecht auf der
Oberfläche
Er ist bei geschlossen Oberflächen nach
außen gerichtet
Feld einer Punktladung
Feld einer unendlich langen Linienladung
Feld innerhalb einer leitenden Kugel / Hohlkugel
Feld einer unendlich ausgedehnten Ladungsschicht
Feld eines idealen Plattenkondensators
(siehe Rechnungen)
(zunächst im Vakuum)
ΦGes = ∫ D d A = Qinnen
© R. Girwidz
15
1.4 Gaußsches Gesetz
16
1.4 Gaußsches Gesetz
Geladene Kugel (leitend / hohl)
Geladener Stab (leitend / hohl)
© R. Girwidz
© R. Girwidz
17
© R. Girwidz
18
–3
1.4 Gaußsches Gesetz
1.4 Gaußsches Gesetz
Geladener Stab (isolierend, konst. Ladungsdichte)
© R. Girwidz
Geladene Kugel (homogene Ladungsdichte)
19
20
© R. Girwidz
1.4 Gaußsches Gesetz
Millikanversuch, Elementarladung
Feldstärke an Spitzen
ƒ
Millikan (1868-1953), Nobelpreis 1923:
Bestimmung der Elementarladung (1910)
(Rechnung siehe Aufgabe)
ƒ
Weitere Hinweise auf die Elementarladung:
Einzelladungen im B-Feld
Elektrolytische Leitung (kleinste Einheiten)
Schwankungserscheinungen bei el. Strömen
© R. Girwidz
21
Anwendungen
© R. Girwidz
© R. Girwidz
22
Anwendungen
23
© R. Girwidz
24
–4
Anwendungen
© R. Girwidz
Anwendungen
25
© R. Girwidz
26
–5